
Сопротивление материалов (часть I)
.pdf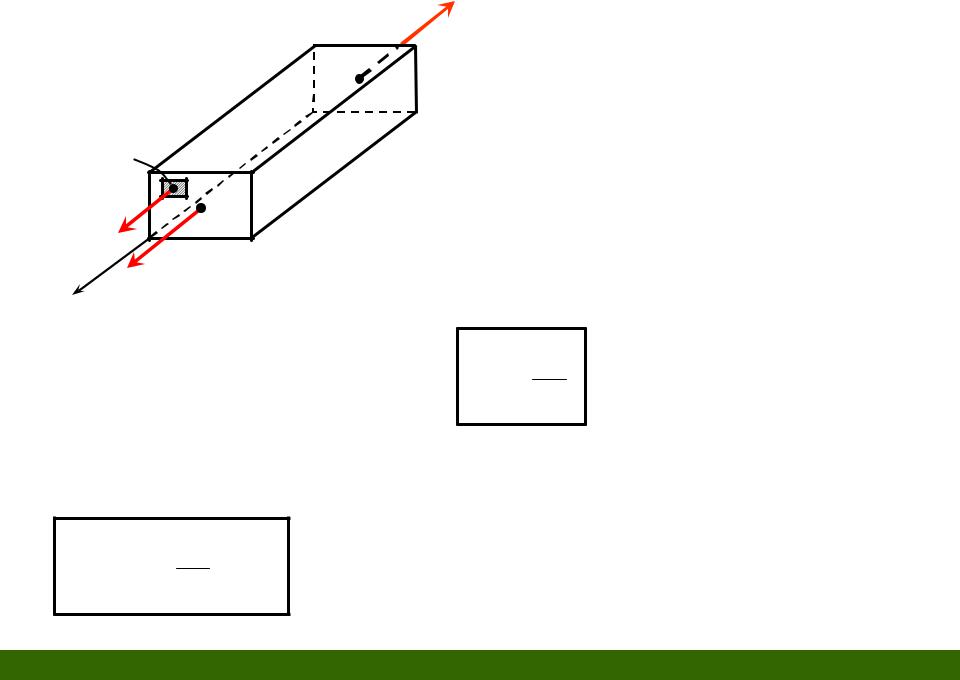
dA
dN
N
x
N dA A
A
F
Fx 0
N F 0; |
N F |
dN dA |
const, |
N A
Условие прочности при растяжении и сжатии
N
max A R
Сопротивление материалов. Растяжение-сжатие (6)

Три типа задач сопротивления материалов
1. Проверочный расчет
max Nmax R
A
2. Проектный расчет
A Nmax
R
3.Определение предельной нагрузки
Nmax A R
Сопротивление материалов. Растяжение-сжатие (7)
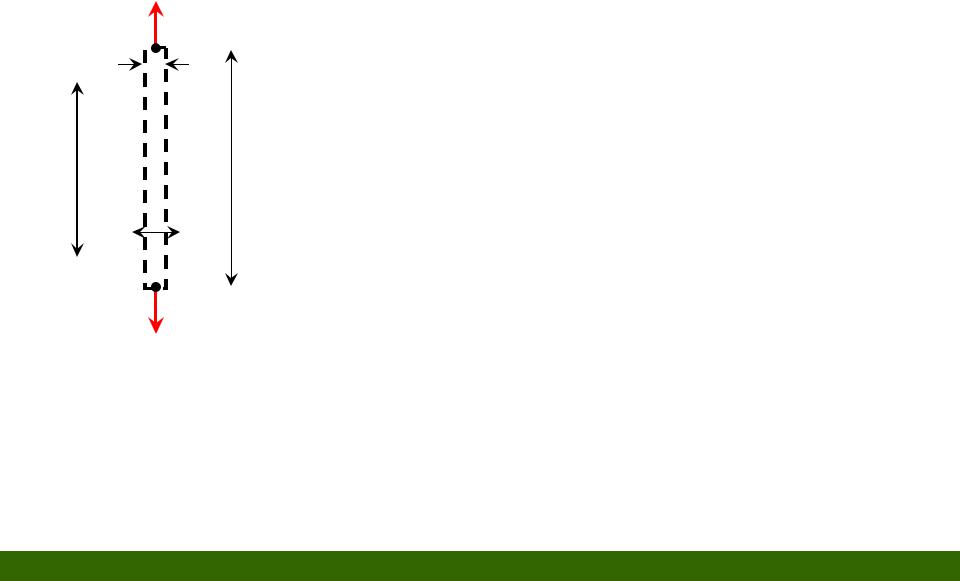
Определение деформаций при растяжении-сжатии
F
|
d |
|
|
|
|
Величина |
0 называется |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
абсолютным удлинением стержня (м, мм). |
|||
0 |
|
|
|
|
|
|
|
|
относительное удлинение |
||||
|
d0 |
|
|
|
|
|
|
|
(безразмерная величина). |
||||
|
|
|
|
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
F |
|
|
|
|
d d0 |
d |
абсолютное изменение |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
диаметра: (м, мм). |
||||
|
и |
положительные, если стержень растягивается, |
|||||||||||
и отрицательные, если стержень сжимается.
Сопротивление материалов. Растяжение-сжатие (8)

Относительное сужение (относительная поперечная деформация)
d d0
Коэффициент поперечной деформации, или коэффициент Пуассона определяется экспериментально.
Опыт показывает, что
Для стали 0,25 0,3 . При приближении стали к пластическому состоянию можно принять, что коэффициент приближается к 0,5.
Сопротивление материалов. Растяжение-сжатие (9)
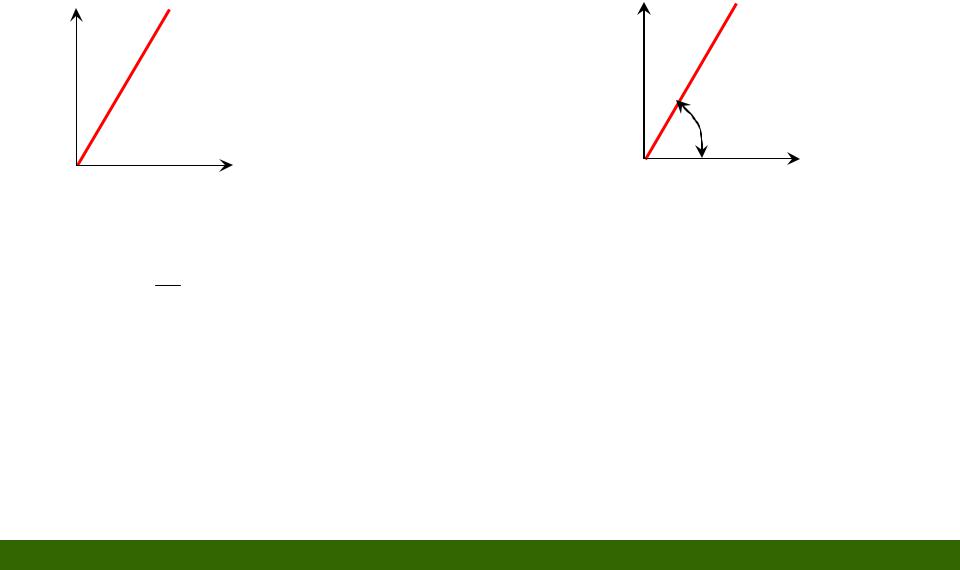
Связь между напряжениями и деформациями
F

tg
|
|
F |
|
|
|
|
|
|
A |
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|||||
0 |
|
|
|
|
|||
|
|
|
|
|
|
||
|
tg E |
E |
|
|
|||
|
|
||||||
|
|
|
|
|
|
||
E модуль упругости первого рода (модуль Юнга), имеет размерность Па
E |
закон Гука |
Сопротивление материалов. Растяжение-сжатие (10)

E ; |
|
N |
; |
|
|||
|
|
A |
|
;
N E A
|
N |
|
EA называют жесткостью стержня при |
EA |
|
растяжении сжатии) |
|
|
|
i ; |
Nxdx |
|
n |
|
|
i 1 |
|
EA(x) |
|
||
Условие жесткости при растяжении и сжатии
umax u
Перемещениемu поперечного сечения стержня называют изменение положения данного сечения по отношению к закрепленному краю или другому сечению.
Сопротивление материалов. Растяжение-сжатие (11)
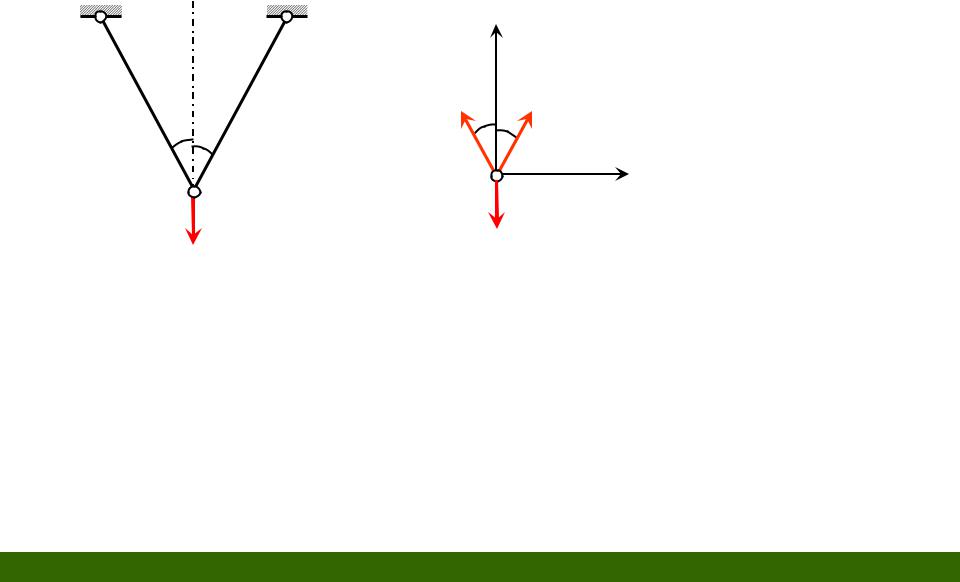
Понятие о статически неопределимых системах
1 |
2 |
|
|
y |
nу 2 |
|
|
|
|||
|
|
N |
N2 |
|
|
|
|
|
|||
|
|
1 |
|
|
nн 2 |
|
|
|
|
x |
|
|
F |
|
|
F |
|
|
|
|
|
|
1)Fx N2 sin N1sin 0
2)Fy N2 cos N1cos F 0
nу |
число уравнений статики |
nн |
число неизвестных усилий |
Сопротивление материалов. Растяжение-сжатие (12)
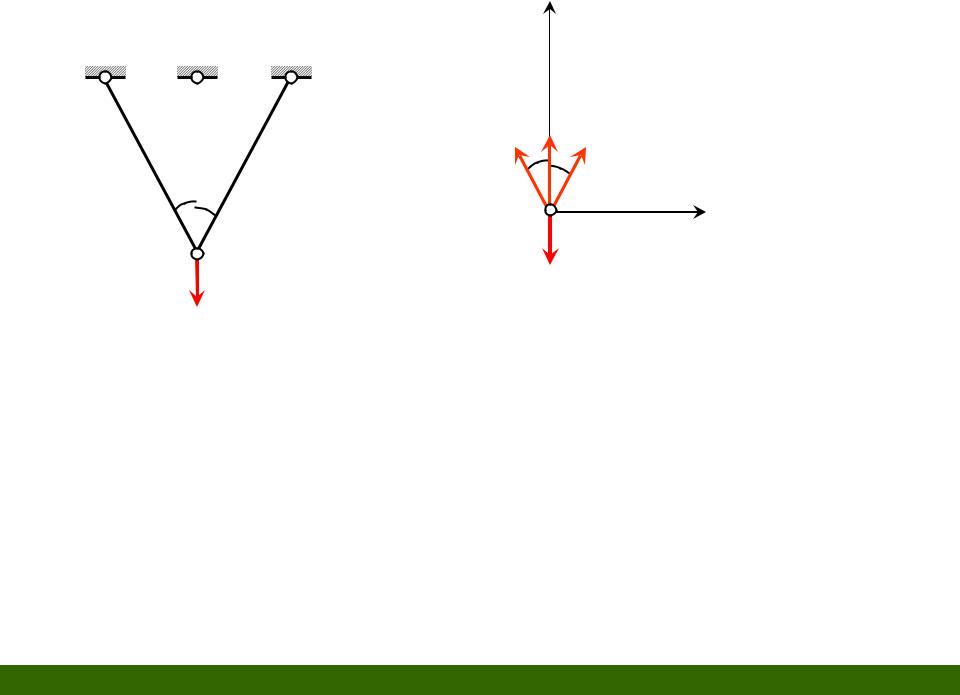
y
1 |
|
3 |
2 |
N1 |
N3 |
nу 2 |
|
|
|
|
N2 |
||
|
|
|
|
|
nн 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
x |
|
|
|
|
|
F
1)Fx N2 sin N1sin 0
2)Fy N2 cos N1cos N3 F 0
n nн nу 3 2 1
Сопротивление материалов. Растяжение-сжатие (13)
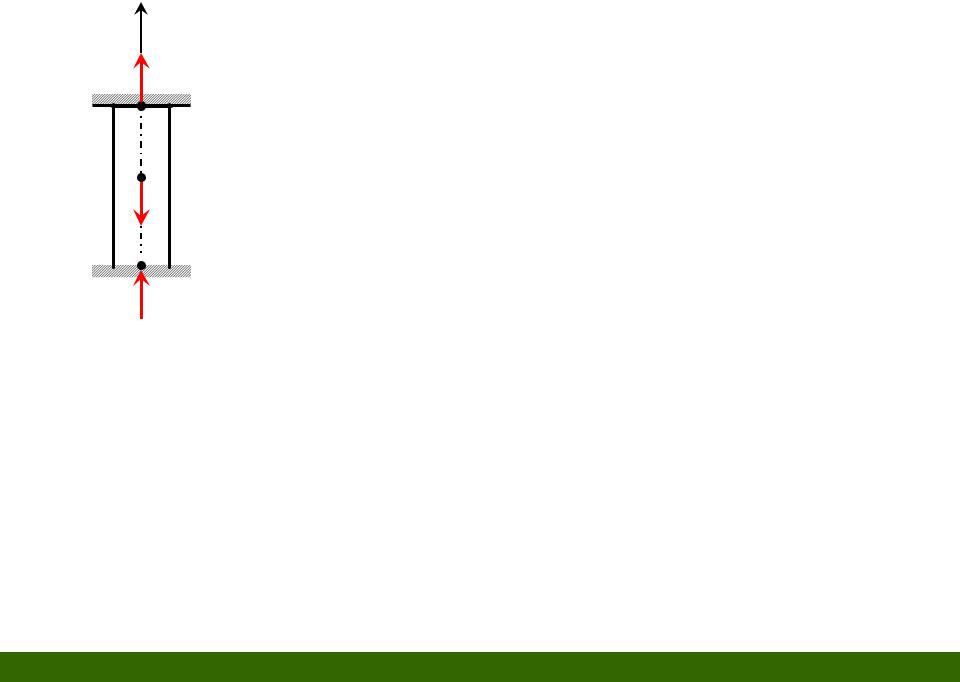
x |
RB, RC ? |
RB B |
Fx RB F RC 0
F
|
nн 2 |
nу 1 |
RС C |
n nн nу 2 1 1 |
|
Расчет статически неопределимых систем
1. Статическая сторона. Для заданной системы записываются возможные уравнения статики, содержащие неизвестные усилия.
Сопротивление материалов. Растяжение-сжатие (14)

2.Геометрическая сторона. Рассматривается схема деформирования системы, и записываются уравнения совместности деформаций, связывающие перемещения характерных сечений и деформации соответствующих элементов системы.
3.Физическая сторона. Используя закон Гука, деформации отдельных элементов системы в уравнениях совместности деформаций выражаются через искомые усилия.
4.Синтез. Решением полученной системы статических, геометрических и физических уравнений, находятся неизвестные усилия.
При рассмотрении статической стороны задачи схему сил и их направления нужно принимать в соответствии с предполагаемой схемой перемещений.
Сопротивление материалов. Растяжение-сжатие (15)
