Задачник по линейной Алгебре и Мат Анализу / Часть 4
.doc4. Введение в анализ
4.1. Сформулировать на языке «
»
окрестностей:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
|
ж)
|
з)
|
и)
|
;
;
;
;
;
;
;
.
4.2. Сформулировать на языке «
»
окрестностей:
|
a)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
|
ж)
|
з)
|
и)
|
;
;
;
;
;
;
;
;
.
4.3.
Доказать, что последовательность
сходится к числу
и указать номер n,
начиная с которого величина
не превосходит заданного положительного
числа
.
4.4. Доказать, используя определение предела числовой последовательности:
-
а)
;б)
.
4.5. Пусть
.
При
имеем
.
Каково должно быть число
,
чтобы из
следовало
?
4.6. Доказать, используя определение предела функции в точке и на бесконечности, что:
-
а)
;б)
.
Вычислить следующие пределы, не применяя правило Лопиталя.
|
4.7.
|
4.8.
|
|
4.9.
|
4.10.
|
|
4.11.
|
4.12.
|
|
4.13.
|
4.14.
|
|
4.15.
|
4.16.
|
|
4.17.
|
4.18.
|
|
4.19.
|
4.20.
|
|
4.21.
|
4.22. |
|
4.23.
|
4.24.
|
|
4.25.
|
4.26.
|
|
4.27.
|
4.28.
|
|
4.29.
|
4.30.
|
|
4.31.
|
4.32.
|
|
4.33.
|
4.34.
|
|
4.35.
|
4.36.
|
|
4.37.
|
4.38.
|
|
4.39. |
4.40. |
|
4.41. |
4.42. |
|
4.43. |
4.44. |
|
4.45. |
4.46. |
|
4.47. |
4.48. |
|
4.49. |
4.50. |
|
4.51. |
4.52. |
|
4.53. |
4.54. |
|
4.55. |
4.56. |
|
4.57. |
4.58. |
|
4.59. |
4.60. |
|
4.61. |
4.62. |
|
4.63. |
4.64. |
|
4.65. |
4.66. |
|
4.67. |
4.68. |
|
4.69. |
4.70. |
|
4.71. |
4.72. |
|
4.73. |
4.74. |
|
4.75. |
4.76. |
|
4.77. |
4.78. |
|
4.79. |
4.80. |
|
4.81. |
4.82. |
|
4.83. |
4.84. |
|
4.85. |
4.86. |
|
4.87. |
4.88. |
|
4.89. |
4.90. |
|
4.91. |
4.92. |
|
4.93. |
4.94. |
|
4.95.
|
4.96.
|
|
4.97.
|
4.98.
|
|
4.99.
|
4.100.
|
|
4.101.
|
4.102.
|
|
4.103.
|
4.104.
|
|
4.105.
|
4.106.
|
|
4.107.
|
4.108.
|
|
4.109.
|
4.110.
|
|
4.111.
|
4.112.
|
|
4.113.
|
4.114.
|
|
4.115.
|
4.116.
|
|
4.117.
|
4.118.
|
|
4.119.
|
4.120.
|
|
4.121.
|
4.122.
|
|
4.123.
|
4.124.
|
|
4.125.
|
4.126.
|
|
4.127.
|
4.128.
|
|
4.129.
|
4.130.
|
|
4.131.
|
4.132.
|
|
4.133.
|
4.134.
|
|
4.135.
|
4.136.
|
|
4.137.
|
4.138.
|
|
4.139.
|
4.140.
|
|
4.141.
|
4.142.
|
|
4.143.
|
4.144.
|
|
4.145.
|
4.146.
|
|
4.147.
|
4.148.
|
|
4.149.
|
4.150.
|
|
4.151.
|
4.152.
|
|
4.153.
|
4.154.
|
|
4.155.
|
4.156.
|
|
4.157.
|
4.158.
|
|
4.159.
|
4.160.
|
|
4.161.
|
4.162.
|
|
4.163.
|
4.164.
|
|
4.165.
|
4.166.
|
|
4.167.
|
4.168.
|
|
4.169.
|
4.170.
|
|
4.171.
|
4.172.
|
|
4.173.
|
4.174.
|
|
4.175.
|
4.176.
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.4.177. Функция f(x) не определена при x=0. Каким должно быть значение f(0), чтобы доопределенная этим значением функция стала непрерывной при x=0:
-
а)
;б)
;в)
;г)
.
Исследовать функции на непрерывность и указать характер точек разрыва.
|
4.178.
|
4.179.
|
|
4.180.
|
4.181.
|
|
4.182.
|
4.183.
|
|
4.184.
|
4.185.
|
|
4.186.
|
4.187.
|
|
4.188.
|
4.189.
|
|
4.190.
|
4.191.
|
|
4.192.
|
4.193.
|
|
4.194.
|
4.195.
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Ответы
4.7.
7. 4.8.
.4.9.
4.10. .4.11.
0.
4.12.
.
4.13.
.
4.14. 0. 4.15.
–0,25. 4.16.
0. 4.17..
4.18. 0.
4.19. .
4.20. 7/27.
4.21. –1. 4.22.
9.
4.23. 1.
4.24. 0.
4.25. 2.
4.26. +2.
4.27. 0.
4.28. 3.
4.29. –1.
4.30.
.
4.31. 1.
4.32. –1.
4.33. 0.
4.34. 4/3.
4.35. -1/2.
4.36.
.
4.37. 0.
4.38. 0,5.
4.39. 1. 4.40.
1/2. 4.41. 0.
4.42. .
4.43. 1/2.
4.44. 1.
4.45. –1/24.46.
(n–k)/2.
4.47. 0.
4.48. 3.
4.49. 0.
4.50. 12.
4.51. 7/3.
4.52. –1.
4.53. 3/2. 4.54.
3. 4.55.
–1/4. 4.56.
.
4.57. 1.
4.58. 0.
4.59.
6/5. 4.60.
–1/7. 4.61.
–11/75. 4.62. 6.
4.63.
48/29. 4.64.
2/3. 4.65. –6.
4.66.
1/3. 4.67.
m/n.
4.68. 0.
4.69. 9/19. 4.70.
7/12. 4.71.
22/5. 4.72.
7/8. 4.73.
4/9. 4.74.
5/23. 4.75.0,25.
4.76. 3.
4.77. –1.
4.78. –6.
4.79.
.
4.80.
1/6. 4.81.
1/4. 4.82. 0,5.
4.83.
7/12. 4.84. 0.
4.85.
1/3. 4.86.
.
4.87.
21/8. 4.88.
–1/6. 4.89.
–1/4. 4.90. 3.
4.91.
1/4. 4.92.
1/2. 4.93.
1/16. 4.94. 7.
4.95. 0,1.
4.96.
1/18. 4.97. 6.
4.98.
4/3. 4.99.
12/5. 4.100.
1/24. 4.101.
1/4. 4.102.
2/3. 4.103.
1/4. 4.104.
k.
4.105.
k/l.
4.106. 32/3.
4.107.
k.
4.108.
2/5. 4.109.
6.
.4.110.
3/2. 4.111.
5/3. 4.112.
25/14. 4.113.
-1.
4.114.
1/2. 4.115.
2/3.
4.116.
1.
4.117.
.
4.118.
1/2. 4.119.
25/9. 4.120.
1/4. 4.121.
–1/.
4.122.
.
4.123.
1/2.
4.124.
1.
4.125.
2/.
4.126.
1.
4.127.
0.
4.128.
0.
4.129.
1/2. 4.130.
e–1.
4.131.
e2/3.
4.132.
e2.
4.133.
e1/3.
4.134.
e–1.
4.135.
e2.
4.136.
e4.
4.137.
e–3.
4.138.
e–2/3.
4.139.
e2/3.
4.140.
e–1/2.
4.141.
e2.
4.142.
2.
4.143.
e–2.
4.144.
e2.
4.145.
e–1.
4.146.
ln2. 4.147.
.
4.148.
ln5–0,5. 4.149.
1.
4.150. e6.
4.151. 1. 4.152.
e–1/.
4.153. –2.
4.154. 1.
4.155. –3.
4.156.
1/2. 4.157.
e–1/2.
4.158. 2/3. 4.159.
lna.
4.160. –1/2.
4.161. 1.
4.162.
1/ln9.
4.163. 1.
4.164.
lna.
4.165. 1.
4.166.
1/2. 4.167.
1/9.4.168.
ln2+0,5.
4.169. –1.
4.170. 2.
4.171. 2.
4.172. 3.
4.173.
9/25. 4.174.
e–1.
4.175.
e2.
4.176. 2.
4.177. a)
1,5; б) 2; в) 1; г) e.
4.178. x=-1
– точка
разрыва второго рода.
4.179.
x=
–1 – точка разрыва первого рода
(устранимый разрыв). 4.180.
x=1,
x=0
– точки разрыва первого рода (устранимый
разрыв), x=
–1 – точка разрыва второго рода
(бесконечный разрыв). 4.181.
x=0
– точка разрыва первого рода (устранимый
разрыв), x=k,
kZ,
–
точки разрыва второго рода (бесконечный
разрыв). 4.182.
x=2
– точки разрыва первого рода (устранимый
разрыв).
4.183. x=0
– точка разрыва второго рода.
4.184. x=5
–точка разрыва второго рода.
4.185. x=4
– точка разрыва второго рода
4.186. x=2
– точка разрыва второго рода.
4.187. x=
–2 – точка разрыва второго рода.
4.188. x=2,
x=5
- точки разрыва второго рода.
4.189. x=3
– точка разрыва второго рода. 4.190.
x=0,
x=
–4 – точки разрыва второго рода.
4.191. x=1,
x=2
– точки разрыва второго рода.
4.192. x=
–2 – точка непрерывности, х=0
– точка разрыва первого рода (конечный
разрыв). 4.193.
х=
–
- точка непрерывности, х=0
– точка разрыва первого рода (конечный
разрыв).
4.194. х=2
– точка непрерывности, х=–
2 – точка разрыва первого рода (конечный
разрыв). 4.195.
х=0
– точка непрерывности, х=/2
– точка разрыва второго род .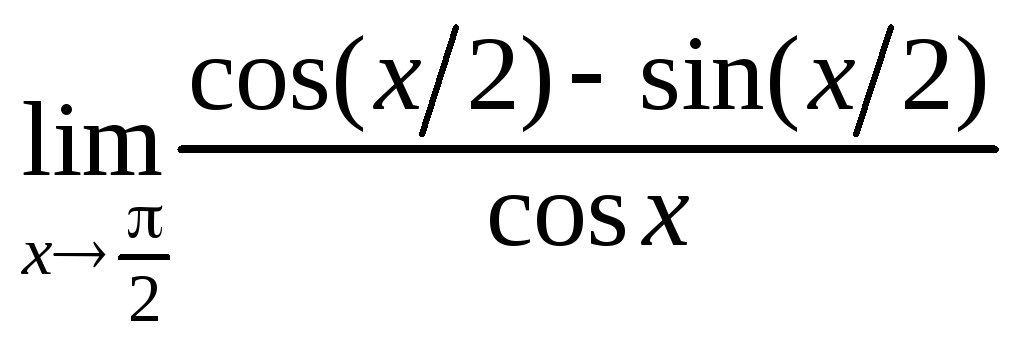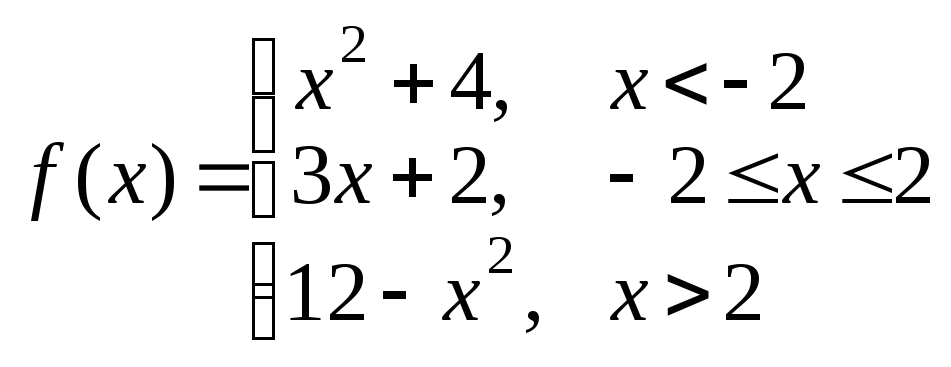