Полярные уравнения кривых второго порядка
Определить, какие линии даны следующими уравнениями в полярных координатах:
1)
2)
3)
4)
5)
6)
Преобразовать к полярным координатам уравнения линий:
1)
;2)
3)
4)
5)
6)
Написать канонические уравнения кривых второго порядка:
1)
2)
3)
Дано уравнение эллипса
Составить его полярное уравнение,
считая, что направление полярной оси
совпадает с положительным направлением
оси абсцисс, а полюс находится:
1) в левом фокусе эллипса;
2) в правом фокусе.
Дано уравнение гиперболы
Составить полярное уравнение ее правой
ветви, считая, что направление полярной
оси совпадет с положительным направлением
оси абсцисс, а полюс находится:
1) в правом фокусе гиперболы;
2) в левом фокусе.
Дано уравнение гиперболы
Составить полярное уравнение ее левой
ветви, считая, что направление оси
совпадает с положительным направлением
оси абсцисс, а полюс находится:
1) в левом фокусе гиперболы;
2) в правом фокусе.
Дано уравнение параболы y2=6x. Составить ее полярное уравнение, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в фокусе параболы.
Геометрические места точек (гмт)
Написать уравнение траектории точки М(x;y), которая при своем движении остается втрое дальше от точкиА(0;9), чем от точкиВ(0;1).
Написать уравнение гмт, сумма расстояний, каждой из которых от точек F1(2;0) иF2(-2;0) равна
.
Построить линию.Написать уравнение гмт, равноудаленных от точки F(2;2) и от осиOx. Построить линию.
Написать уравнение гмт, разность расстояний каждой из которых от точек F1(–2;–2) иF2(2;2) равна 4. Построить линию.
Дана окружность
Из точки ееА(–2;0) проведена хордаАВи продолжена на расстояниеВМ=АВ. Определить гмтМ.Определить траекторию точки М, которая при своем движении остается вдвое ближе к точкеF(–1;0), чем к прямой
.Определить траекторию точки М, которая при своем движении остается втрое ближе к точкеА(1;0), чем к прямойx=9.
Дана точка А(a;0). По осиOyдвижется точкаВ. На прямойВЕ, параллельной осиOx, откладываются отрезкиВМиВМ1, равныеАВ. Определить гмтМиМ1.
Определить траекторию точки М, которая движется так, что остается вдвое дальше от точкиF(–8;0), чем от прямойx=–2.
Из вершины параболы
проведены всевозможные хорды. Написать
уравнение гмт середин этих хорд.Определить гмт центров окружностей, касающихся окружности
и осиOy.
Поверхности второго порядка
Построить поверхности второго порядка:
1)
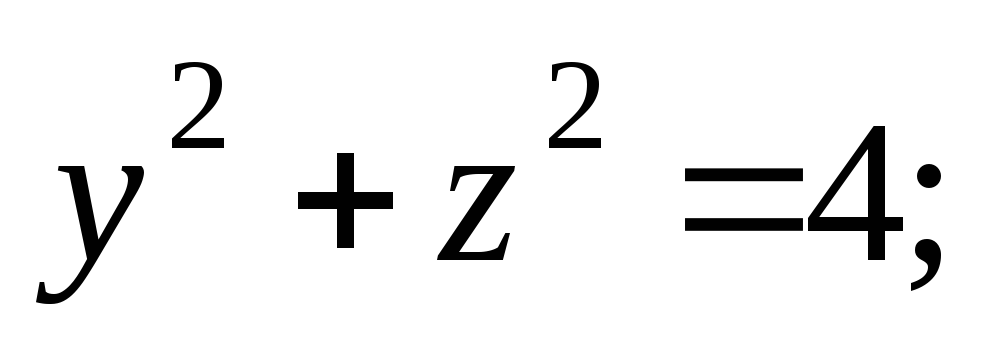
2)
3)
4)
Построить тело, ограниченное поверхностями y2=x,z=0,z=4,x=4 и написать уравнения диагоналей грани, лежащей в плоскостиx=4.
Построить поверхность
и найти площади ее сечений плоскостями:
а)z=3; б)y=1.Построить поверхности: 1) x2+y2–z2=4; 2)x2–y2+z2+4=0.
Построить гиперболоид
и найти его образующие через точку
(4;1;–3).Построить поверхность
и найти ее образующие, проходящие через
точку (3;1;2).В прямоугольной системе координат изобразить тело, ограниченное указанными поверхностями:
1)
2)
3)
4)
5)
6)
7)
Ответы
3.1.
3.2.
.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
BC:
x+2y–1=0; CA:
x–y–1=0;
mA:x–3=0;
mB:x+y–3=0;
mC:
y=0.
3.9.
3.10.
3x–4y+15=0;
4x+3y–30=0;
3x–4y–10=0;
3.11.
3.12.
S=6
ед2.
3.13.
3x–2y–12=0;
3x–8y+24=0.
3.14.
S=5
кв.ед.
3.15.
d=4.
3.16.
1)
2,5; 2) 3; 3) 0,5; 4) 3,5. 3.17.
.
3.18.
.
3.19.
.
3.20.
3.21.
.
3.22.
.
3.23.
.
3.24.
или
3.25.
3.26.
3.27. 
3.28.
3.29.
3.30.
3.31.
3.32.
3.33.
3.34. 1)
600
и 1200;
2) 450
и 1350;
3) 900.
3.35.
3.36.
3.37.
3.38.
3.39.
3.40.V=8
ед3.
3.41.
3.42. d=4.
3.43. V=8
ед3.
3.44.
3.45.
и
3.46.
3.47.
.3.48.
.3.49.
.3.50. 
cos=
=0,3
;
3.51.
3.52.
3.53.
3.54.
3.55.
3.56.
3.57.
3.58.
.
3.59.
.
3.63.
.
3.65.
3.66.
3.67.
3.68.
3.69.
3.70.
3.71.
3.72.
3.73.
3.74.
3.75.
3.76.
.
3.77.
.
3.80.1) 13;
2)
3.81.
3.82.
3.83.
3.84.
3.85.
3.86.
.3.87.
3.88.
3.89. 
3.90. 900.
3. 91.
3.92.
3.93.
3.94.
3.95.
и
3.96.
3.97.
;
5)
.3.98.
или 
3.99.
и
3.100.
3.101. 3
и 7. 3.102.
.
3.103. 
3.104.
3.105.
3.106.
3.107.
3.108.
или
3.109. 
3.110.
3.111.
3.112. 
4.113.
10. 3.114. 
3.115.
3.116.
3.117.
3.118.
3.119. (0;0)
и
.3.122. 
3.123. 
3.124.
3.125.
3.126.
3.127.
3.128.
3.129.
3.130.
3.131.
3.132.
3.134. 1)
эллипс; 2) парабола; 3) ветвь гиперболы;
4) эллипс; 5) ветвь гиперболы; 6) парабола.
3.135. 
3.136.
3.137.
3.138.
.
3.139.
3.140.
3.141.
3.142.
3.143.
3.144.
3.145.
3.146
3.147.
3.148.
3.149.
3.150.
3.151.
и
3.152.
3.154.
3.156.
и
3.157.
