Гипербола

87. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:

1) ее оси 2а=10, 2b=8;

2) расстояние между фокусами 2с=10 и ось 2b=8;

3) расстояние между фокусами 2с=6 и эксцентриситетε=1,5;

4) ось 2а=16 и эксцентриситетε=1,25;

5) уравнение асимптот и расстояние между фокусами 2с=20;

6) расстояние между директрисами равнои расстояние между фокусами 2с=26;

7) расстояние между директрисами равно 32/5 и ось 2b=6;

8) расстояние между директрисами равно 8/3 и эксцентриситет ε=1,5;

9)уравнение асимптот y=(3/4)xи расстояние между директрисами равно 12,8.

87. Дана гипербола . Найти:

1) полуоси аиb;

2) фокусы;

3) эксцентриситет;

4) уравнения асимптот;

5) уравнения директрис.

87. Эксцентриситет гиперболы ε=2, центр ее лежит в начале координат, один из фокусовF(12;0). Вычислить расстояние от точкиМ₁гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.

88. Составить уравнение гиперболы, зная, что:

1) расстояние между ее вершинами равно24 и фокусы суть F₁(–10;2),F₂(16;2);

2) фокусы суть F₁(3;4),F₂(–3;–4) и расстояние между директрисами равно 3, 6;

3) угол между асимптотами равен 90⁰и фокусы сутьF₁(4;–4),F₂(–2;2).

87. Доказать, что расстояние от фокуса гиперболы до ее асимптоты равноb.

88. Доказать, что произведение расстояний от любой точки гиперболы 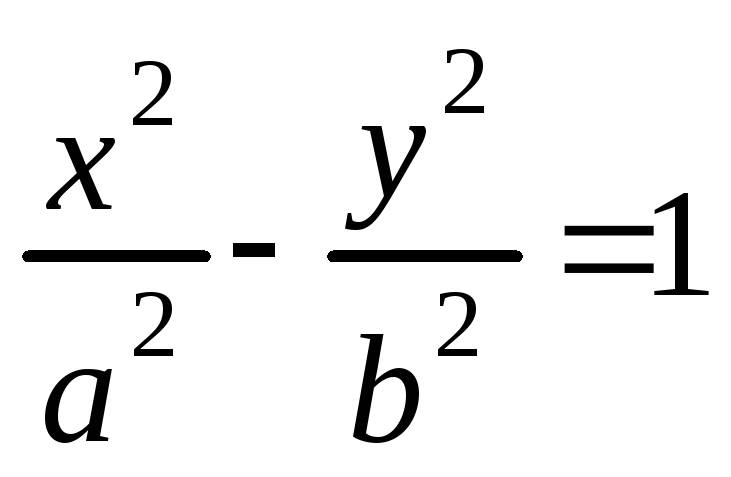до двух ее асимптот есть величина постоянная, равная .

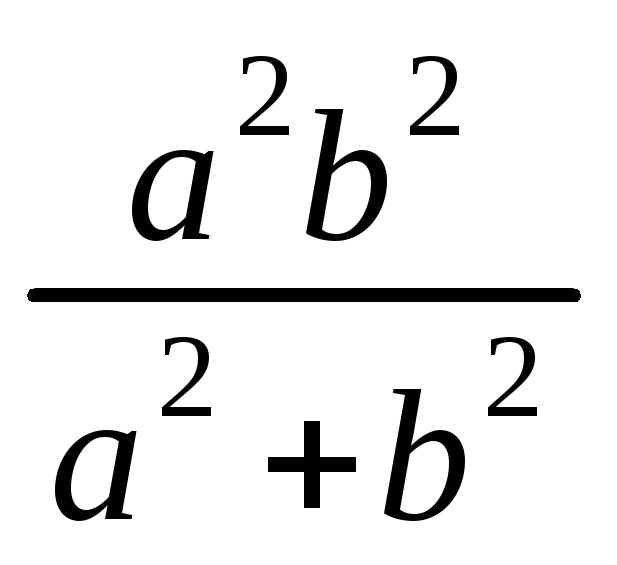89. Построить гиперболу и ее асимптоты. Найти фокусы, эксцентриситет и угол между асимптотами.

90. Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса

91. Найти расстояние фокуса гиперболы 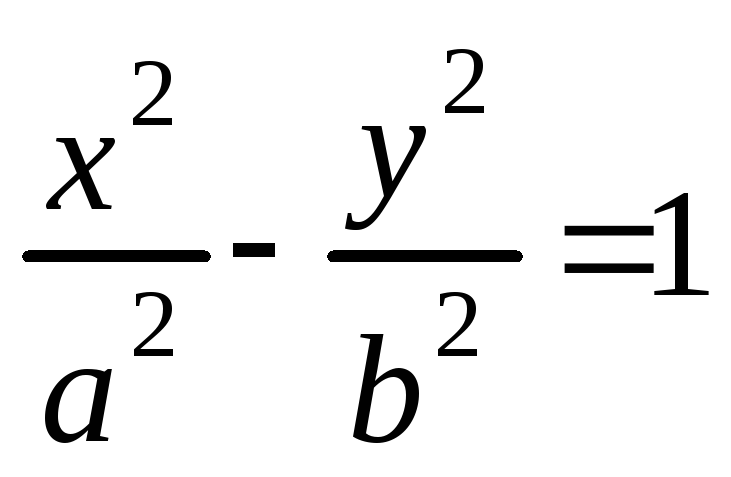от ее асимптот и угол между асимптотами.

92. Определить траекторию точки М(x;y), которая при своем движении остается вдвое ближе к прямойx=1, чем к точкеF(4;0).

93. Найти точки пересечения асимптот гиперболы с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

Парабола

87. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола расположена в правой полуплоскости симметрично относительно оси Ox, и ее параметрp=3;

2) парабола расположена в левой полуплоскости симметрично оси Ox, и ее параметрp=0,5;

3) парабола расположена в верхней полуплоскости симметрично оси Oy, и ее параметр ;

4) парабола расположена в нижней полуплоскости симметрично относительно оси Oy, и ее параметрp=3.

87. Определить величину параметра и расположение относительно координатных осей следующих парабол: 1) y²=6x; 2)x²=5y; 3)y²=–4x; 4)x²=–y.

88. Составить уравнение параболы, которая имеет фокус F(0;–3) и проходит через начало координат, зная, что ее осью служит осьOy.

89. Найти фокус Fи уравнение директрисы параболы

90. Составить уравнение параболы, если дан фокус F(–7;0) и уравнение директрисыx–7=0.

91. Составить уравнение параболы, если дан фокус F(2;–1) и уравнение директрисыx–y–1=0.

92. Построить параболы, заданные уравнениями: 1) y²=4x; 2)y²= – 4x; 3)x²=4y; 4)x²= – 4y, а также их фокусы и директрисы и написать уравнения директрис.

93. Написать уравнение параболы:

1) проходящей через точки (0;0) и (1;–3) и симметричной относительно оси Ox;

2) проходящей через точки (0;0) и (2;–4) и симметрично относительно оси Oy.

87. Написать уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой x+y=0 и окружностии симметрична осиOy. Построить окружность, прямую и параболу.

88. В параболу y²=2xвписан правильный треугольник. Определить его вершины.

89. Написать уравнения касательных к параболе y²=8x, проведенных из точкиА(0;–2).

90. Через фокус параболы y²=–4xпроведена прямая под углом 120⁰к осиOx. Написать уравнение прямой и найти длину образовавшейся хорды.