Задачник по линейной Алгебре и Мат Анализу / Часть 10

10. КРАТНЫЕ ИНТЕГРАЛЫ

Вычислить повторные интегралы:

10.1. .	10.2. .
10.3. .	10.4. .
10.5. .	10.6. .
10.7. .	10.8. .
10.9. .	10.10. .
10.11. .	10.12. .

Для данных повторных интегралов написать уравнения кривых, ограничивающих области интегрирования, и построить эти области:

10.13. .	10.14. .
10.15. .	10.16. .

Определить пределы интегрирования для интеграла , где область интегрирования ограничена линиями:

10.17.	10.18.
10.19.	10.20.
10.21.

Изменить порядок интегрирования:

10.22. .	10.23. .
10.24. .	10.25. .
10.26. .	10.27. .
10.28. .	10.29. .

10.30. .

10.31. .

10.32. .

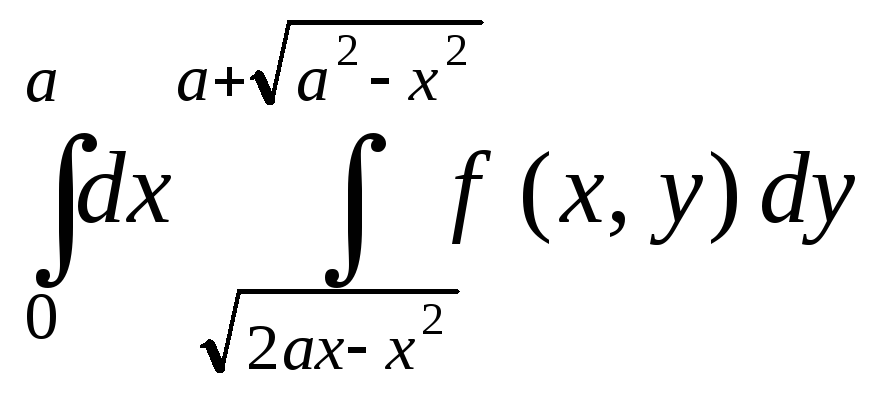10.33. .

10.34. .

Перейдя к полярным координатам, вычислить следующие интегралы:

10.35. .	10.36. .
10.37. .	10.38. .

10.39. , где область G – кольцо между двумя окружностями и .

10.40. .

10.41. , где область G – часть круга радиуса a с центром в точке О (0, 0), лежащая в первой четверти.

10.42. .

10.43. , где область G ограничена кривыми , , .

10.44. , где область G ограничена кривыми , , .

10.45. , где область G ограничена лепестком лемнискаты .

Вычисление площадей посредством двойного интеграла.

46. .

47. 

48. .

49. 

50. .

51. Найти площадь фигуры, ограниченной кривыми y²=4ax+4a² и x+y=2a (a>0).

52. Вычислить площадь фигуры, ограниченной параболой y²=2x и прямой y=x.

53. Найти площадь фигуры, ограниченной кривыми xy=4 и x+y=5.

54. Вычислить площадь фигуры, ограниченной линиями y²=4ax, x+y=3a, y=0.

55. Найти площадь фигуры, ограниченной кривыми , x=2y, x=0 (a>0).

56. Найти площадь фигуры, ограниченной линиями x^1/2+y^1/2=a^1/2, x+y=a.

57. Найти площадь фигуры, ограниченной кривыми r=a(1–cos) и r=a (вне кардиоиды).

58. Вычислить площадь фигуры, ограниченной линиями y=sinx, y=cosx, x=0.

59. 

60. 

61. Найти площадь части плоскости , вырезаемой цилиндром y²=ax и плоскостью x=a.

62. Вычислить площадь петли кривой =asin2.

63. Найти площадь части поверхности цилиндра x²+z²=a², вы-

резаемой цилиндром y²=a (a–x).

46. Вычислить всю площадь, ограниченную лемнискатой ²=a²cos2.

47. Найти площадь части поверхности конуса x²+z²=y², вырезаемой цилиндром y2=2px.

48. Вычислить площадь петли кривой .

Указание. Перейти к новым переменным x=acos и y=bsin.

46. Найти полную поверхность тела, ограниченного цилиндрами x²=ay, z²=ay, и плоскостью y=2a (a>0).

47. Найти площадь части поверхности конуса x²+z²=y², вырезаемой плоскостями x=0, x–y=2a, y=0.

48. Найти площадь части поверхности цилиндра x²+y²=2ax, вырезаемой цилиндром z²=2a(2a–x).

49. Найти площадь части сферы x²+y²+z²=2a², заключенной внутри конуса x²+y²=z².

50. Найти площадь части поверхности параболоида z=x²–y², заключенной между параболоидами z=3x²+y²–2 и z=3x²+y²–4.

51. Найти площадь части сферы x²+y²+z²=a², вырезаемой цилиндром с образующими, параллельными оси OZ, направляющий которого служит трехлепестковая роза r=asin3.

52. Найти площадь части винтовой поверхности z=aarctg(x/y), вырезаемой цилиндром x²+y²=a².

Найти объемы тел, ограниченных поверхностями:

46. .

47. .

48. , .

49. , , , .

50. , , .

51. , , .

52. , , (внутри цилиндра; ).

53. , , .

54. , .

55. , , .

56. , .

57. , , , .

58. , .

59. , , (внутри конуса; , , ).

60. Найти объем тела, ограниченный координатными плоскостями, плоскостью и цилиндром .

61. Найти объем тела, ограниченный круговым цилиндром радиуса , ось которого совпадает с осью OZ, плоскостями координат и плоскостью .

62. Определить центр тяжести площади, ограниченной линиями .

63. Найти центр тяжести площади, ограниченной одной петлей кривой .

64. Определить координаты центра тяжести фигуры, ограниченной линиями .

65. Определить координаты центра тяжести полуэллипса , отсеченного осью .

66. Определить момент инерции площади ограниченной линиями: относительно оси .

67. Определить момент инерции площади ограниченной линиями: относительно оси .

68. Определить момент инерции площади ограниченной линиями: .

69. Определить момент инерции относительно оси площади треугольника с вершинами .

70. Вычислить момент инерции относительно оси фигуры, ограниченной кардиоидой .

71. Вычислить полярный момент инерции фигур, ограниченной линиями.

72. .

Тройные интегралы.

Расставить пределы интегрирования в тройном интеграле для указанных областей Т:

46. Область Т – тетраэдр, ограниченный плоскостями 2x+3y+4z=12, , , .

47. Область Т – внутренность эллипсоида .

48. Область Т ограничена поверхностями , .

49. Область Т ограничена поверхностями , .

Вычислить интегралы

46. Вычислить , если область интегрирования ограничена координатными плоскостями и плоскостью .

47. Вычислить

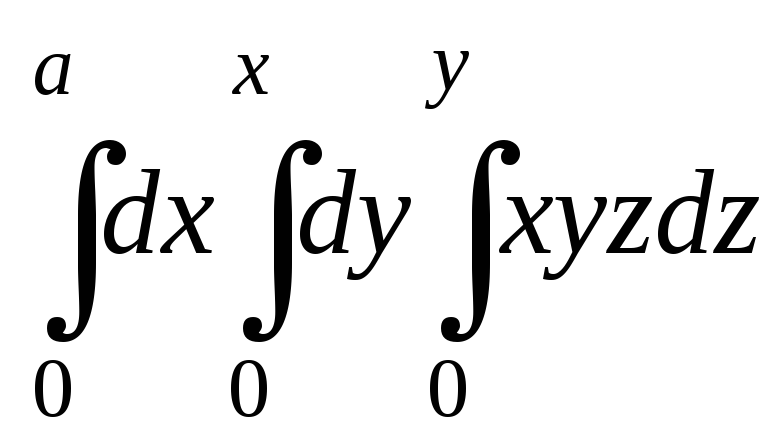
48. Вычислить объем тела, ограниченного сферой x²+y²+z²=4 и поверхностью параболоида x²+y²=3z.

49. Вычислить объем тела, ограниченного поверхностями .

50. Вычислить объем тела, ограниченного плоскостью , цилиндрической поверхностью и сферой (внутри цилиндра).

51. Определить объем тел, ограниченных поверхностями: .

52. Определить объем тел, ограниченных поверхностями: .

53. Определить объем тел, ограниченных поверхностями: .

54. Определить объем тел, ограниченных поверхностями: .

55. Определить объем тел, ограниченных поверхностями: .

56. Вычислить момент инерции кругового прямого конуса относительно его оси.

Примечание: в задачах 8.88, 8.90 - 8.92 считаем плотность постоянной и равной 1)

46. Вычислить объем тела, ограниченного поверхностью с уравнением (x²+y²+z²)²=a³x.

47. Вычислить момент инерции круглого конуса относительно диаметра основания.

48. Вычислить координаты центра тяжести тела, содержащегося между сферой радиуса a и конической поверхностью с углом при вершине 2, если вершина конуса совпадает с центром сферы.

49. Вычислить координаты центра тяжести тела, ограниченного сферой радиуса a и двумя плоскостями, проходящими через центр сферы и образующими угол в 60⁰.

50. Найти координаты центра масс полушара x²+y²+z²≤R², если плотность в каждой точке пропорциональна расстоянию от точки до центра.

Вычислить интегралы:

46. .

47. .

48. .

49. , где область Т – тетраэдр, ограниченный плоскостями x+y+z=a, x=0, y=0, z=0.

50. , где область Т ограничена поверхностями y=x², x=y², z=xy, z=0.

51. , где область Т ограничена поверхностями z=y²–x², z=0, y=1.

Вычислить координаты, перейдя к цилиндрическим координатам:

46. , где область Т ограничена поверхностями x²+y²=a², z=0, z=h.

47. , где область Т ограничена поверхностями x²+y²=z², z=a.

48. , где область ограниченна поверхностями: .

49. , где область ограничена плоскостями:

Ответы

10.1. 8/3. 10.2. . 10.3. /6. 10.4. ln (25/24). 10.5. (1/2)ln(14/11). 10.6. 15/4. 10.7. a²/4(+4). 10.8. (1/2)a². 10.9. 3/2. 10.10. arctg. 10.11. . 10.12. . 10.13. y=x, y=x+3, x=1, x=2. 10.14. y=, y=, x=0, x=1. 10.15. x+y=2, x=, y=0, y=2. 10.16. . 10.17. . 10.18. . 10.19. . 10.20. . 10.21. . 10.22. . 10.23. . 10.24. 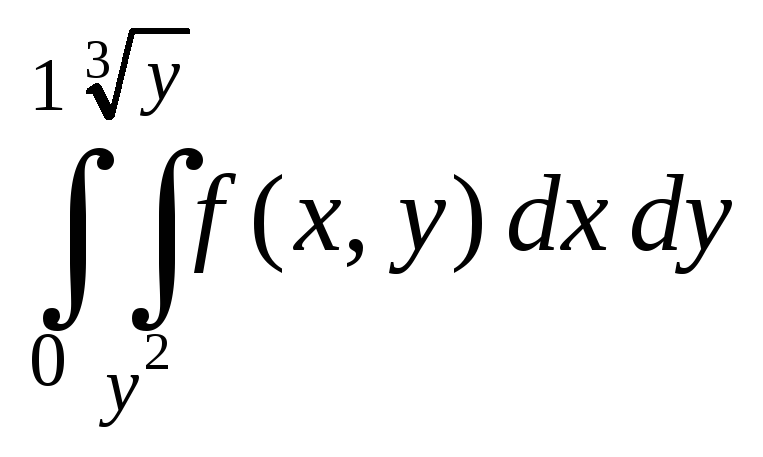. 10.25. . 10.26. . 10.27. .10.28. . 10.29. . 10.30. . 10.31. . 10.32. . 10.33. . 10.34. .

10.35. . 10.36. . 10.37. (2/9)a³. 10.38. . 10.39. . 10.40. . 10.41.. 10.42. . 10.43. . 10.44. . 10.45. . 10.46. . 10.47. . 10.48. . 10.49. . 10.50.. 10.51. . 10.52. . 10.53. . 10.54. . 10.55. . 10.56. . 10.57. . 10.58. . 10.59. . 10.60. . 10.61. 10.62. . 10.63. . 10.64. . 10.65. . 10.66. . 10.67. . 10.68. . 10.69. . 10.70. . 10.71. . 10.72. . 10.73. .10.74. . 10.75. 10.76. . 10.77. . 10.78. . 10.79. . 10.80. . 10.81. . 10.82. . 10.83. . 10.84. . 10.85. 549/144. 10.86. . 10.87. . 10.88. 16. 10.89. . 10.90. . 10.91. . 10.92. . 10.93. . 10.94. . 10.95. . 10.96. . 10.97. . 10.98. .10.99. . 10.100. . 10.101. . 10.102. . 10.103. . 10.104. . 10.105. . 10.106. . 10.107. . 10.108. . 10.109. .10.110. .10.111. . 10.112. . 10.113. . 10.114. . 10.115. , где - высота, - радиус основания конуса. 10.116 . 10.117. . 10.118. , , (ось конуса принята за ось Oz, вершина помещена в начале координат.) 10.119. , , (линия пересечения плоскостей принята за ось Oz, центр сферы - за начало координат; , ,  – сферические координаты). 10.120. ). 10.121. 1/6. 10.122. 81/4. 10.123. a⁴/12. 10.124. a⁴/8. 10.125. 1/96. 10.126. 4/15. 10.127. . 10.128. (a⁴)/h. 10.129. . 10.130. 4.