
Задачник по линейной Алгебре и Мат Анализу / Часть 2
.doc2. Векторная алгебра
Линейные операции над векторами
-
Угол между векторами
 и
и
 равен
300. Построить векторы
равен
300. Построить векторы
 и
и
 .
. -
Вычислить модуль вектора
 .
. -
Даны две координаты вектора
 Определить его третью координату z
при условии, что
Определить его третью координату z
при условии, что

-
Даны точки А(3;–1;2) и В(–1;2;1). Найти координаты векторов
 и
и
 .
. -
Определить начало вектора
 если его конец совпадает с точкой
(1;–1;2).
если его конец совпадает с точкой
(1;–1;2). -
Вычислить направляющие косинусы вектора

-
Дан модуль вектора
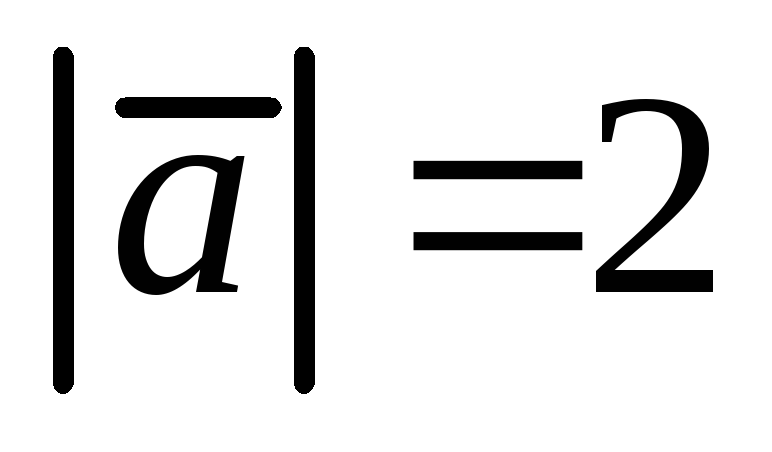 и углы
и углы
 которые он составляет с осями координат.
Найти координаты вектора
которые он составляет с осями координат.
Найти координаты вектора
 .
. -
Может ли вектор составлять с координатными осями следующие углы 1)

2)
![]()
3)
![]() ?
?
-
Вектор составляет с осями Ох и Oz углы
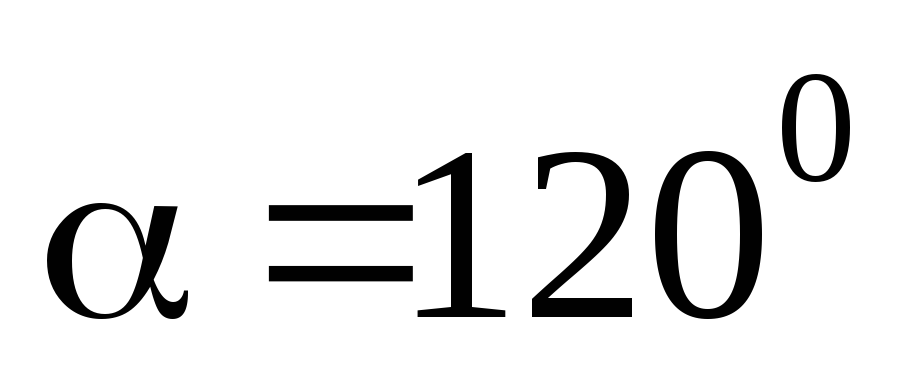 и
и
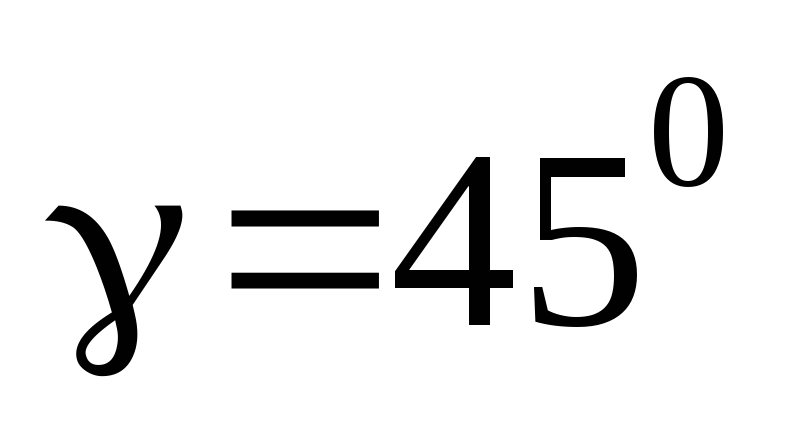 .
Какой угол он составляет с осью Oy?
.
Какой угол он составляет с осью Oy? -
Вектор
 составляет с осями Ох и Oy
углы
составляет с осями Ох и Oy
углы
 и
и
 .
Вычислить его координаты при условии,
что
.
Вычислить его координаты при условии,
что
 .
. -
Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.
-
Точка
 является центром тяжести
является центром тяжести
 .
Доказать, что
.
Доказать, что
 .
. -
В треугольной пирамиде
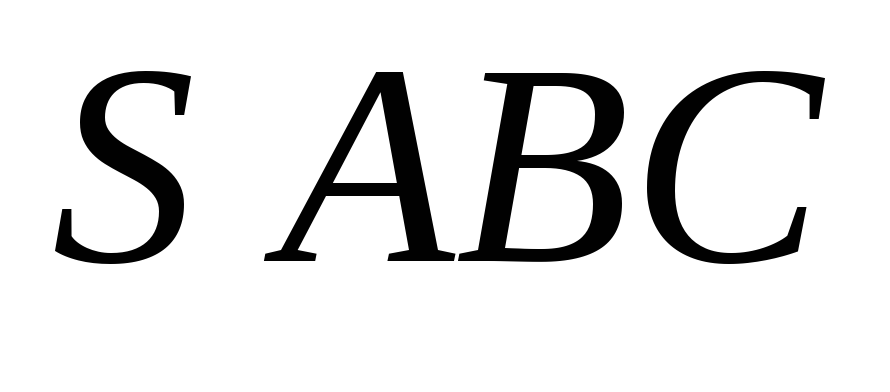 даны векторы
даны векторы
 ,
,
 ,
,
 .
Найти вектор
.
Найти вектор
 ,
где
,
где
 – точка пересечения медиан
– точка пересечения медиан
 .
. -
Какому условию удовлетворяют векторы
 и
и
 ,
если вектор
,
если вектор
 направлен по биссектрисе между ними?
направлен по биссектрисе между ними? -
Даны
 Вычислить
Вычислить

-
Векторы
 и
и
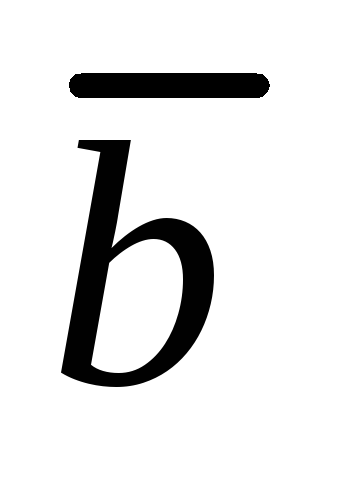 образует
угол
образует
угол
 ,
причем
,
причем
 Определить
Определить
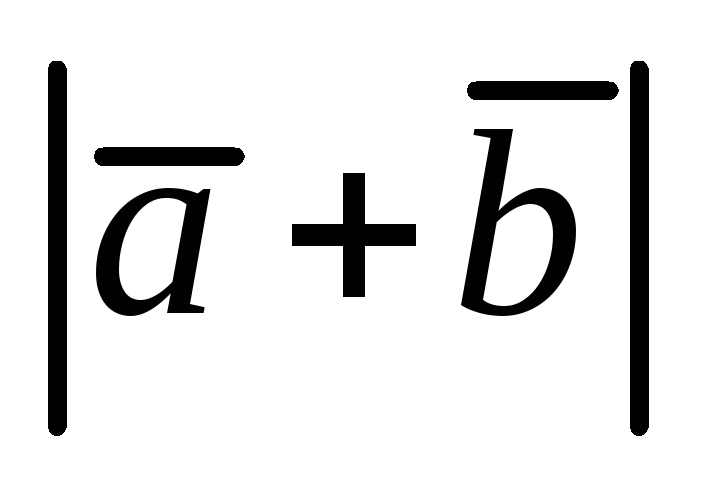 и
и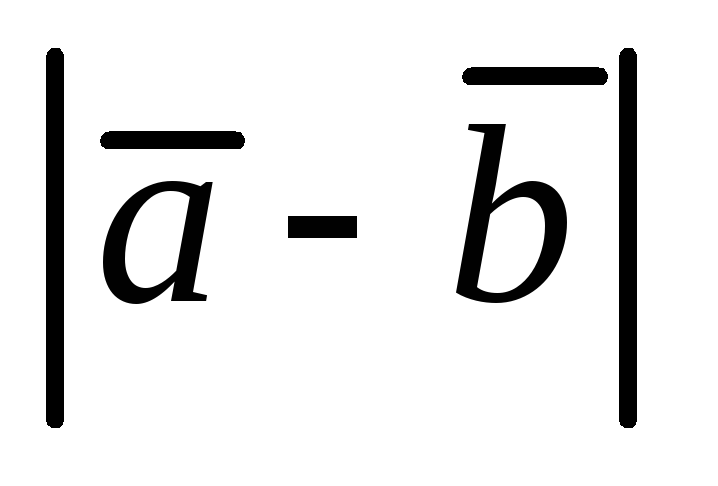 .
. -
Определить при каких значениях
 и
и
 векторы
векторы
 =
–2i+3j+k
и
=
–2i+3j+k
и
 коллинеарны.
коллинеарны. -
Найти орт вектора
 .
. -
Определить модули суммы и разности векторов
 и
и
 .
. -
Даны три вектора
 Определить разложение вектора
Определить разложение вектора
 по базису векторов
по базису векторов
 и
и
 .
. -
Даны три вектора
 Найти разложение вектора
Найти разложение вектора
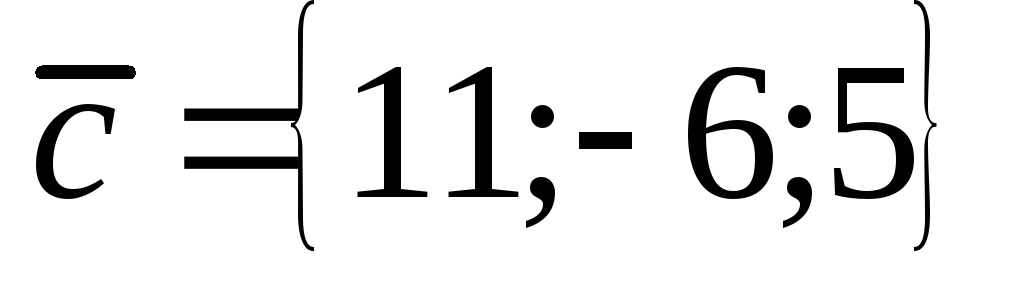 по базису
по базису
 .
. -
Даны четыре вектора
 и
и
 Определить разложение вектора
Определить разложение вектора
 по базису
по базису

Скалярное произведение двух векторов
-
Векторы
 и
и
 образуют угол
образуют угол
 .
Зная, что
.
Зная, что

 вычислить: 1)
вычислить: 1)
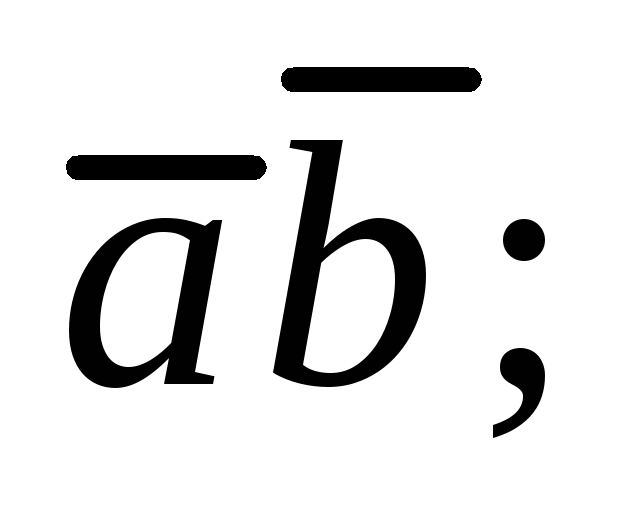 2)
2)
 3)
3)
 4)
4)

5)
![]()
![]() 6)
6)
![]() 7)
7)
![]()
-
Даны единичные векторы
 удовлетворяющие
условию
удовлетворяющие
условию
 Вычислить
Вычислить
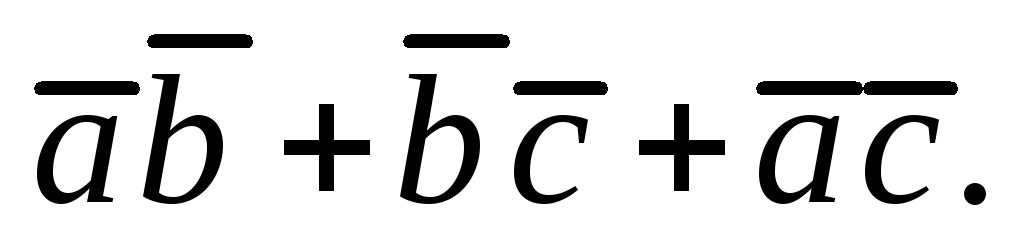
-
Векторы
 попарно
образуют друг с другом углы, каждый из
которых равен 600. Зная, что
попарно
образуют друг с другом углы, каждый из
которых равен 600. Зная, что
 и
и
 определить
модуль вектора
определить
модуль вектора
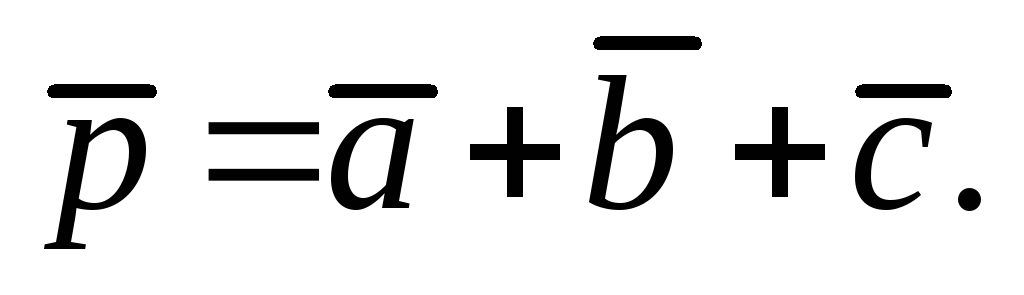
-
Дано, что
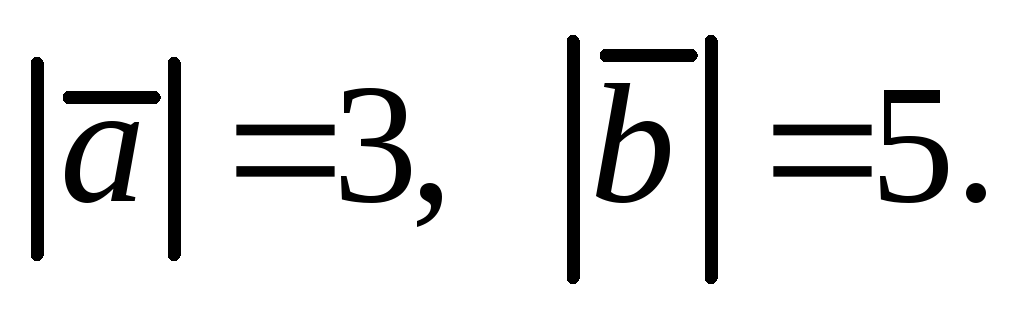 Определить при каком значении
Определить при каком значении
 векторы
векторы
 и
и
 будут взаимно перпендикулярны.
будут взаимно перпендикулярны. -
Какому условию должны удовлетворять векторы
 и
и
 ,
чтобы вектор
,
чтобы вектор
 был перпендикулярен вектору
был перпендикулярен вектору ?
? -
Определить угол между векторами
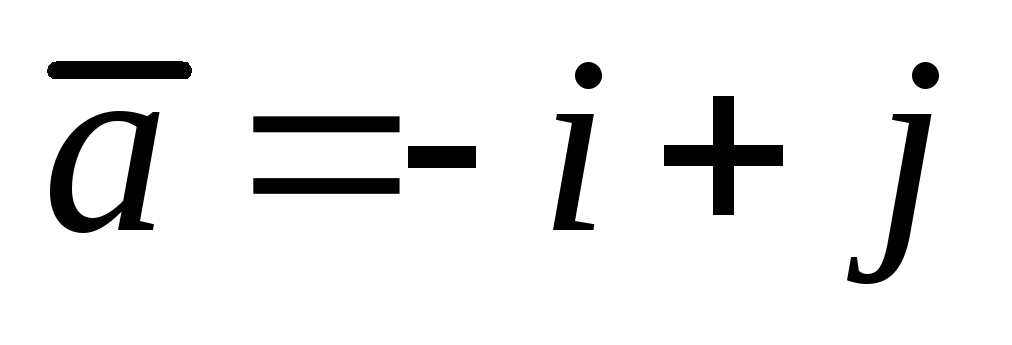 и
и

-
Даны вершины треугольника
 ,
,
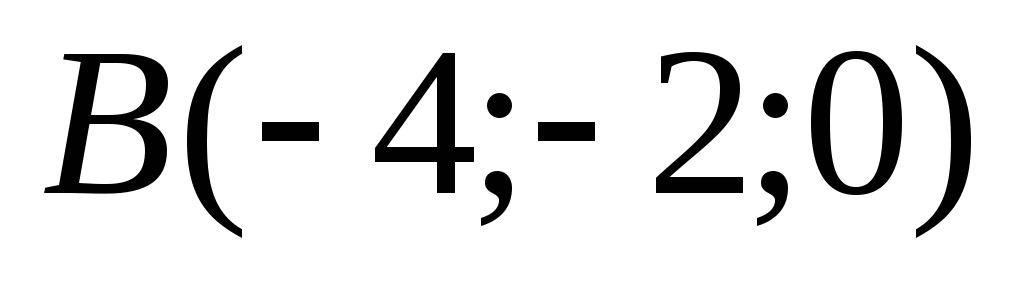 ,
,
 .
Найти его внутренний угол
.
Найти его внутренний угол
 при вершине
при вершине
 и внешний угол
и внешний угол
 при вершине
при вершине
 .
. -
Найти вектор
 ,
перпендикулярный векторам
,
перпендикулярный векторам
 и
и
 ,
если известно, что его проекция на
вектор
,
если известно, что его проекция на
вектор
 равна 1.
равна 1. -
Определить углы
 с вершинами А(2;-1;3), В(1;1;1) и
С(0;0;5).
с вершинами А(2;-1;3), В(1;1;1) и
С(0;0;5). -
На плоскости дан
 и
и
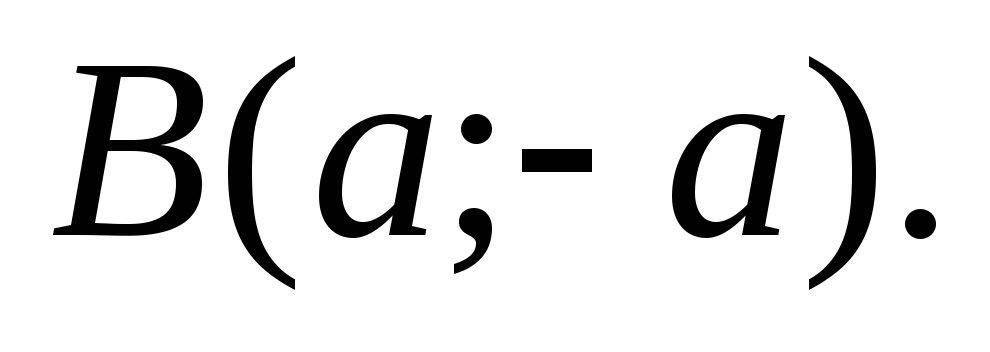 Найти угол, образованный стороной ОВ
и медианой ОМ этого треугольника.
Найти угол, образованный стороной ОВ
и медианой ОМ этого треугольника. -
Найти угол между биссектрисами углов xOy и YOZ.
-
Из вершины квадрата проведены прямые делящие противоположные стороны пополам. Найти угол между этими прямыми.
-
Найти угол между диагоналями параллелограмма, построенного на векторах
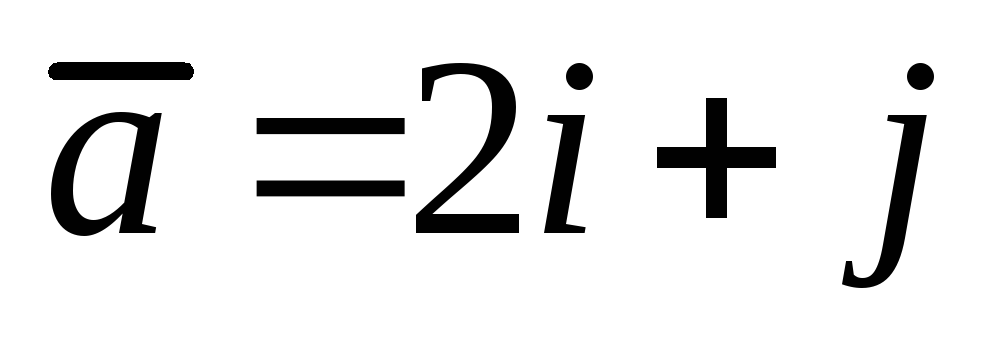 и
и

-
Раскрыть скобки и вычислить

-
Даны векторы
 и
и
 Найти пр
Найти пр
 и пр
и пр
 .
. -
Даны три вектора
 и
и
 Вычислить пр
Вычислить пр

-
Даны три вектора
 и
и
 .
Вычислить пр
.
Вычислить пр
 .
. -
Вычислить какую работу производит сила
 когда
ее точка приложения, двигаясь
прямолинейно, перемещается из положения
А(2;–3;5) в положение В(3;–2;–1).
когда
ее точка приложения, двигаясь
прямолинейно, перемещается из положения
А(2;–3;5) в положение В(3;–2;–1). -
Даны три силы
 и
и
 приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из точки М1(5;3;–7) в точку
М2(4;–1;–4).
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из точки М1(5;3;–7) в точку
М2(4;–1;–4).
Векторное произведение двух векторов
-
Раскрыть скобки и упростить выражения:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
-
Векторы
 и
и
 образуют угол
образуют угол
 .
Зная, что
.
Зная, что
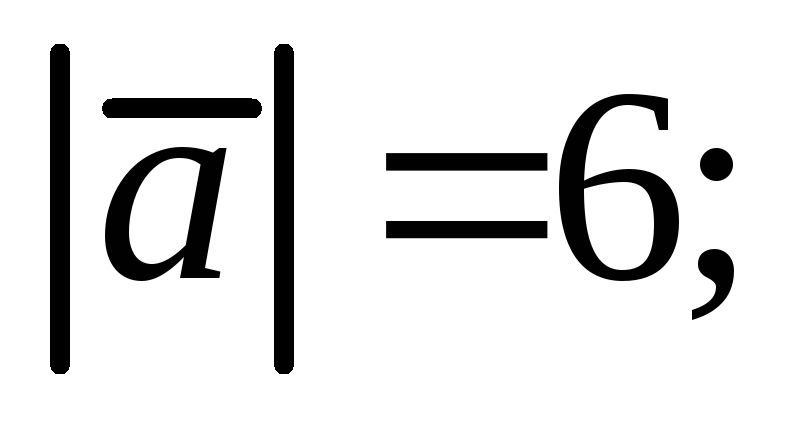
 .
Вычислить
.
Вычислить

-
Даны:
 и
и
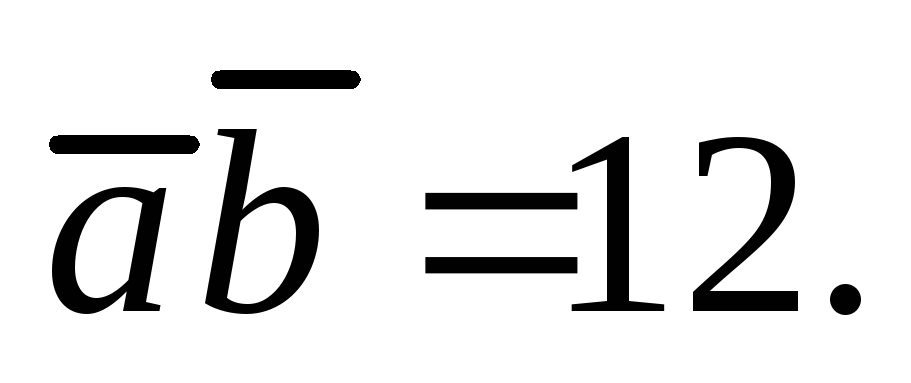 Вычислить
Вычислить
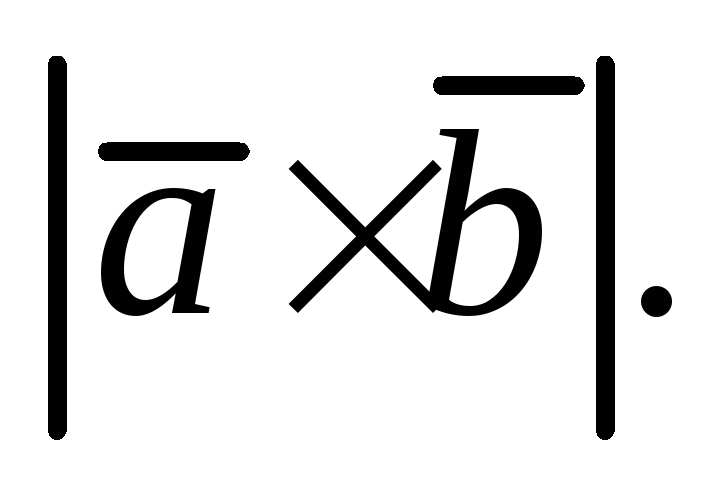
-
Даны:
 и
и
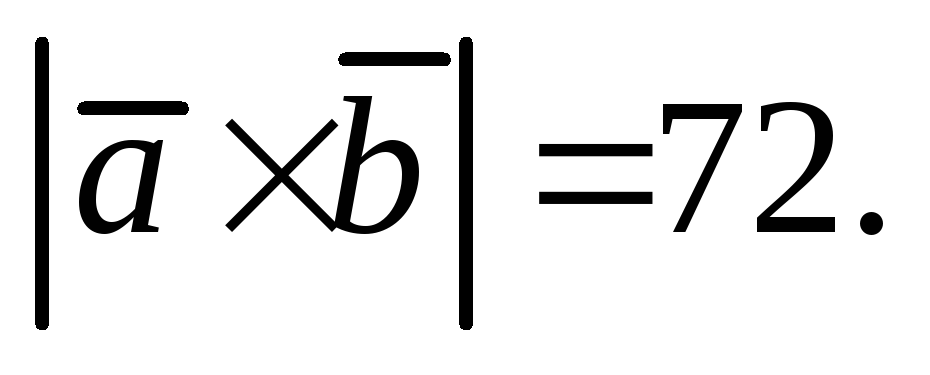 Найти
Найти

-
Векторы
 и
и
 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что

 вычислить: 1)
вычислить: 1)
 2)
2)
 .
. -
Векторы
 удовлетворяют условию
удовлетворяют условию
 .
Доказать, что
.
Доказать, что
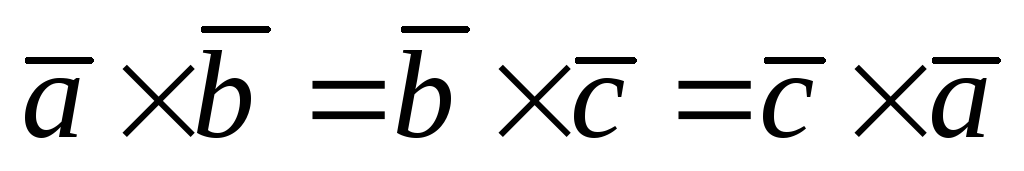 .
. -
Упростить выражение
 .
. -
Доказать тождество
 .
. -
Какому условию должны удовлетворять векторы
 и
и
 ,
чтобы векторы
,
чтобы векторы
 и
и
 были коллинеарны?
были коллинеарны? -
Даны векторы
 и
и
 .
Найти координаты векторных произведений:
1)
.
Найти координаты векторных произведений:
1) ;
;
2)
![]()
3)
![]()
-
Даны точки А(2;–1;2), В(1;2;–1) и С(3;2;1). Найти координаты векторных произведений:
 2)
2)

-
Сила
 приложена
к точке
приложена
к точке
 Определить момент этой силы относительно
точки
Определить момент этой силы относительно
точки
 .
. -
Сила
 приложена к точке
приложена к точке Определить величину и направляющие
косинусы момента этой силы относительно
точки
Определить величину и направляющие
косинусы момента этой силы относительно
точки

-
Вычислить площадь треугольника с вершинами

 и
и
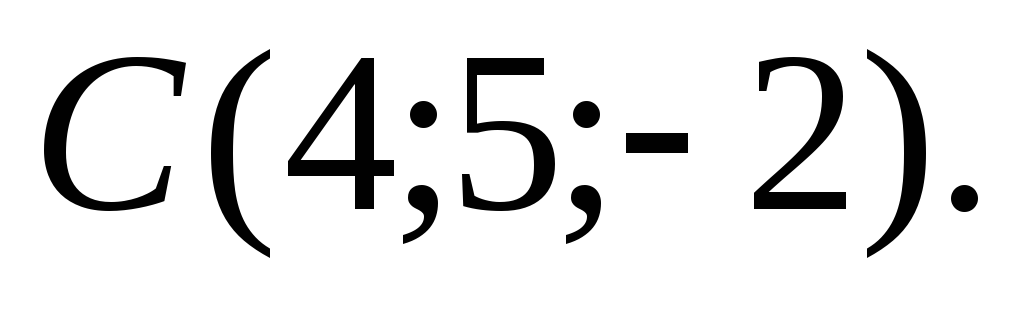
-
Построить параллелограмм на векторах
 и
и
 и вычислить его площадь и высоту.
и вычислить его площадь и высоту. -
Векторы
 и
и
 составляют угол 450. Найти площадь
треугольника, построенного на векторах
составляют угол 450. Найти площадь
треугольника, построенного на векторах
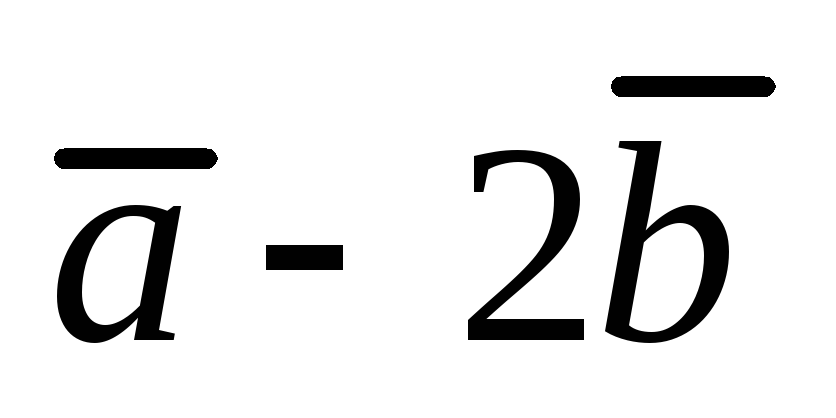 и
и
 ,
если
,
если

-
Построить треугольник с вершинами
 и
и
 Вычислить его площадь и высоту
Вычислить его площадь и высоту
 .
. -
Вычислить диагонали и площадь параллелограмма, построенного на векторах
 и
и
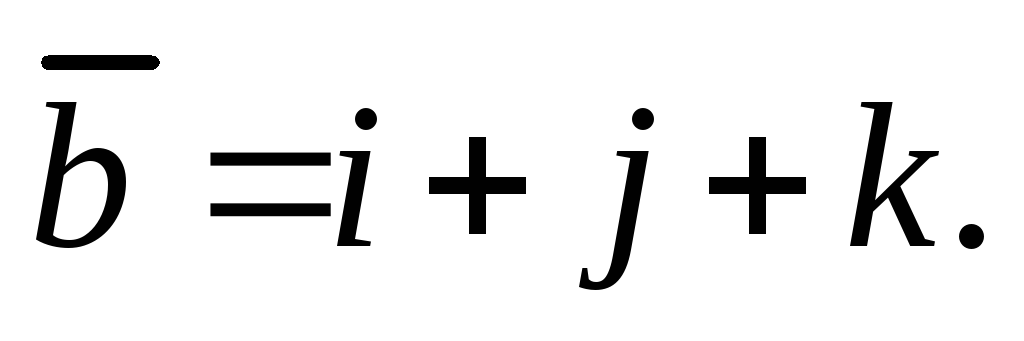
-
Доказать, что
 .
. -
Найти площадь параллелограмма, построенного на векторах
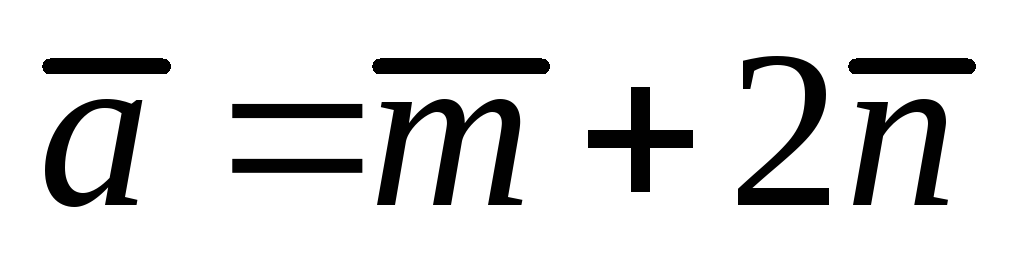 и
и
 где
где
 и
и
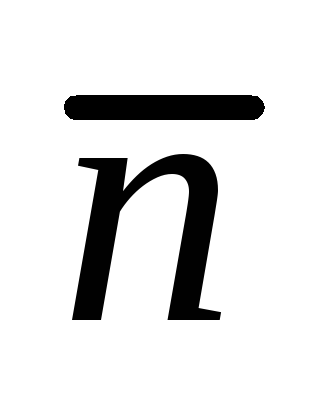 – единичные векторы, образующие угол
300.
– единичные векторы, образующие угол
300. -
Вектор
 ,
перпендикулярный к оси Oz
и к вектору
,
перпендикулярный к оси Oz
и к вектору
 образует острый угол с осью Ox.
Зная, что
образует острый угол с осью Ox.
Зная, что
 найти его координаты.
найти его координаты.
Смешанное произведение трех векторов
-
Показать, что векторы компланарны.
1)
![]()
2)
![]()
3)
![]()
-
Показать, что: 1)

2)
![]()
-
Вектор
 перпендикулярен
к векторам
перпендикулярен
к векторам
 и
и
 угол между
угол между
 и
и
 равен 300. Зная, что
равен 300. Зная, что
 вычислить
вычислить

-
Доказать тождество

-
Даны три вектора
 Вычислить
Вычислить

-
Доказать, что четыре точки
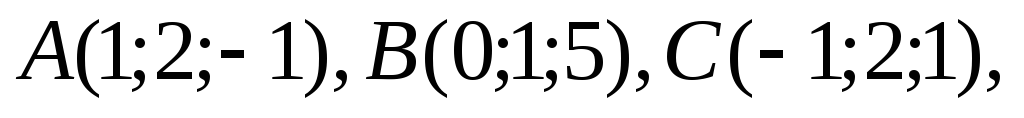
 лежат в одной плоскости.
лежат в одной плоскости. -
Вычислить объем тетраэдра, вершины которого находятся в точках
 и
и

-
Построить пирамиду с вершинами

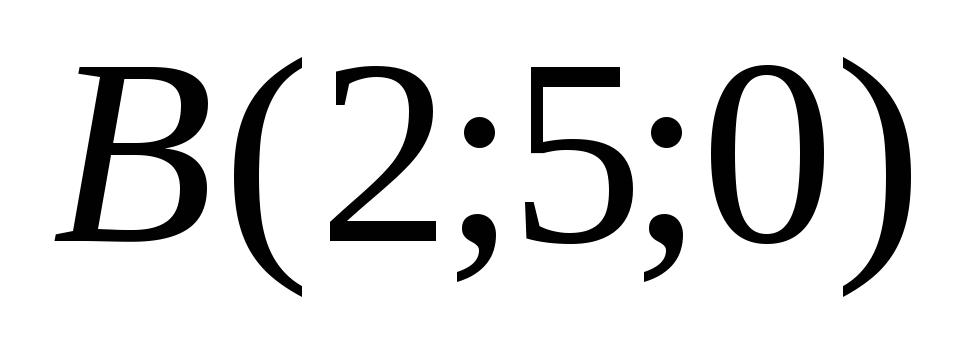 и
и
 и вычислить ее объем, площадь грани
АВС и высоту пирамиды, опущенную
на эту грань.
и вычислить ее объем, площадь грани
АВС и высоту пирамиды, опущенную
на эту грань. -
Построить пирамиду с вершинами А(2;0;0), В(0;3;0) С(0;0;6) и
 ,
вычислить ее объем и высоту, опущенную
на грань АВС.
,
вычислить ее объем и высоту, опущенную
на грань АВС. -
Показать, что объем параллелепипеда, построенного на диагоналях граней данного параллелепипеда, равен удвоенному объему данного параллелепипеда.
-
Объем тетраэдра
 три его вершины находятся в точках
три его вершины находятся в точках
 Найти координаты четвертой вершины
D, если известно, что она
лежит на оси Oy.
Найти координаты четвертой вершины
D, если известно, что она
лежит на оси Oy.
Ответы
2.2.
7.
2.3.
±3.
2.4.
(–4;3;–1);
(4;–3;1). 2.5.
(–1;2;3).
2.6.
![]()
![]()
![]() .
2.7.
.
2.7.
![]() 2.8. 1)
да; 2) нет; 3) да. 2.9.
600
или 1200.
2.10.
2.8. 1)
да; 2) нет; 3) да. 2.9.
600
или 1200.
2.10.
![]() или
или
![]() .
2.11.
.
2.11.
![]() и
и
![]() 2.12.
2.13.
2.12.
2.13.
![]() .
2.14.
.
2.14.
![]() .
2.15. 22.
.
2.15. 22.
2.16.
![]() 2.17.
2.17.
![]() 2.18.
2.18.![]() 2.19.
2.19.![]() 2.20.
2.20.
![]() 2.21.
2.21.
![]() 2.22.
2.22.
![]() 2.23. 1)
–6; 2) 9; 3) 16; 4) 13; 5) –61; 6) 37; 7) 73. 2.24.
–1,5. 2.25.
10. 2.26.
2.23. 1)
–6; 2) 9; 3) 16; 4) 13; 5) –61; 6) 37; 7) 73. 2.24.
–1,5. 2.25.
10. 2.26.
![]() 2.27.
2.27.
![]() 2.28. 1350.2.29.
2.28. 1350.2.29.
![]() .
2.30.
.
2.30.
![]() .
2.31. 450;
450;
900.
2.32.
.
2.31. 450;
450;
900.
2.32.
![]() 2.33. 600..
2.34.
2.33. 600..
2.34.
![]() 2.35. 900.
2.36. 2.
2.37.
2.35. 900.
2.36. 2.
2.37.
![]() 2.38. –4.
2.39. 5.
2.40. 31.
2.41. 13.
2.42. 1)
2.38. –4.
2.39. 5.
2.40. 31.
2.41. 13.
2.42. 1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
3. 2.43. 15.
2.44. 16.
2.45.
4)
3. 2.43. 15.
2.44. 16.
2.45.
![]() 2.46. 1) 24; 2) 60.
2.48.
2.46. 1) 24; 2) 60.
2.48.
![]() .
2.50.
.
2.50.
![]() 2.51. 1)
{5;1;7}; 2) {10;2;14}; 3) {20;4;28}. 2.52.
1)
{6;–4;–6}; 2) {–12;8;12}. 2.53.
{–4;3;4}
2.51. 1)
{5;1;7}; 2) {10;2;14}; 3) {20;4;28}. 2.52.
1)
{6;–4;–6}; 2) {–12;8;12}. 2.53.
{–4;3;4}
2.54.
28;
![]()
![]() 2.55. 24,5.
2.56.
2.55. 24,5.
2.56.
![]() 2.57.
2.57.
![]() 2.58.
2.58.
![]() 2.59.
2.59.
![]() 2.61. 1,5. 2.62.
{45;24;0}.
2.65.
2.61. 1,5. 2.62.
{45;24;0}.
2.65.![]() 2.67. –7.
2.69. 3.
2.70. V=14ед.3,
2.67. –7.
2.69. 3.
2.70. V=14ед.3,
![]()
2.71.
V=14ед.3,
![]() 2.73.
2.73.
![]()
![]()
