Случайные функции Случайные функции
Найти математическое ожидание с.ф.: а)
,
где
-
случайная величина, причем
;
б)
,
где
,
-
случайные величины, причем
,
.Задана корреляционная функция
с.ф.
Найти корреляционные функции с.ф.: а)
;
б)
;
в)
Задана дисперсия
с.ф.
Найти дисперсию с.ф.:
а)
;
б)
.
Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию с.ф.
,
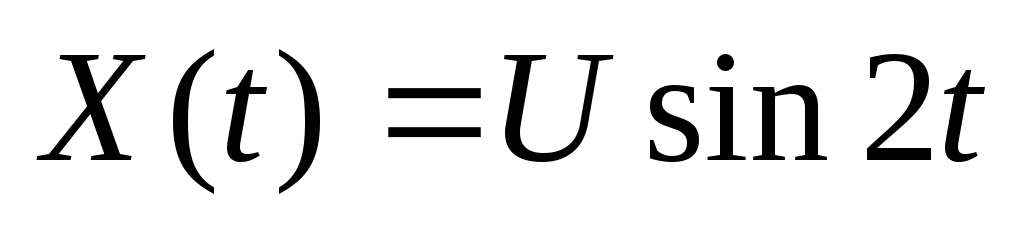где
-
случайная величина, причем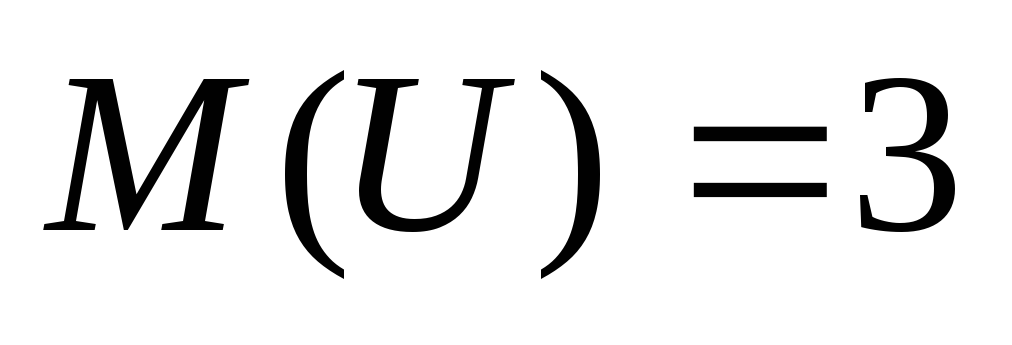
,
.Найти нормированную корреляционную функцию с.ф.
,
зная ее корреляционную функцию
.Найти: а) взаимную корреляционную функцию; б) нормированную взаимную корреляционную функцию двух с.ф.
и
,
где
-
случайная величина, причем
.Задано математическое ожидание
с.ф.
Найти математическое ожидание интеграла
.Задана с.ф.
,
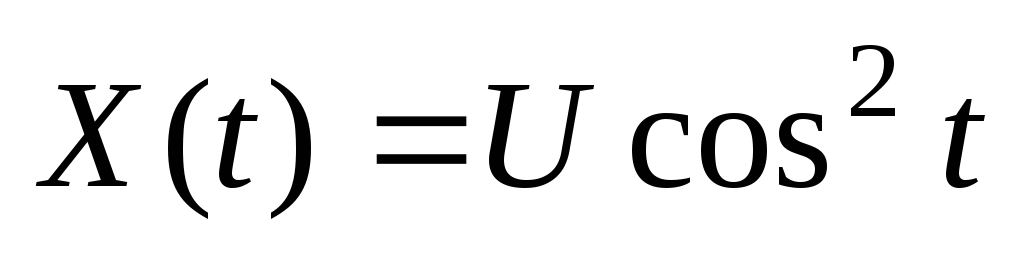где
-
случайная величина, причем
.
Найти математическое ожидание с.ф.
.Задана корреляционная функция
с.ф.
Найти: а) корреляционную функцию; б)
дисперсию интеграла
Стационарные случайные функции
Является ли стационарной с. ф.
где
-
случайная величина, причем: а)
,
б)
?Стационарна ли с.ф.
,
где
- случайная величина, распределенная
равномерно в интервале
?Известно, что если
- случайная величина, распределенная
равномерно в интервале
,
то с.ф.
-
стационарная. Можно ли отсюда
непосредственно заключить, что с.ф.
- стационарная?Задана с.ф.
,
где
,
-
случайные величины, причем
,
,
.
Доказать, что: а)
-
нестационарная функция; б)
-
стационарная функция.Известна корреляционная функция
стационарной с.ф.
.
Найти корреляционную функцию с.ф.
.Задана корреляционная функция
стационарной с.ф.
.
Найти а) корреляционную функцию; б)
дисперсию производной
.Задана корреляционная функция
стационарной с.ф.
.
Найти дисперсию интеграла
Элементы спектральной теории стационарных случайных функций
Найти дисперсию стационарной с.ф.
,
зная ее спектральную плотность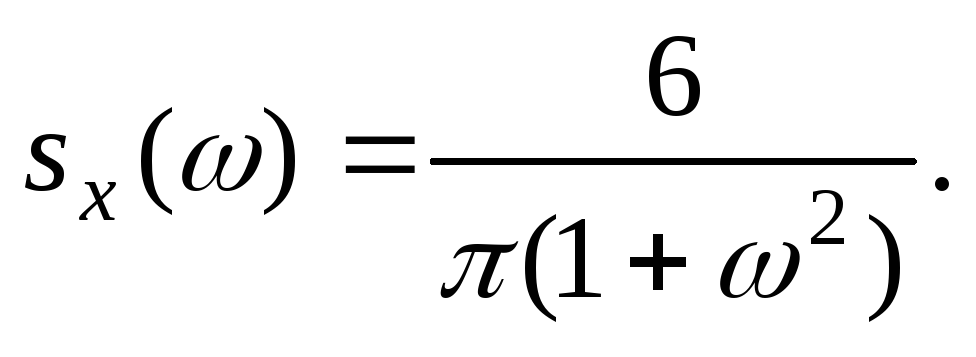
Найти спектральную плотность стационарной с.ф.
,
зная ее корреляционную функцию
Найти спектральную плотность стационарной с.ф.
,
зная ее корреляционную функцию
Задана спектральная плотность
стационарной с.ф.
.
Найти нормированную спектральную
плотность.Найти корреляционную функцию стационарной с.ф.
,
зная ее спектральную плотность
Спектральная плотность стационарной с.ф.
постоянна в диапазоне частот
,
а вне его равна нулю:
Найти:
а) корреляционную функцию; б) дисперсию;
в) нормированную корреляционную функцию
с.ф.
.
На вход линейной стационарной динамической системы, описываемой уравнением
,
подается стационарная с.ф.
с математическим ожиданием
и
корреляционной функции
Найти
математическое ожидание и ее дисперсию
с.ф.
на выходе системы в установившемся
режиме.На вход линейной стационарной динамической системы, описываемой уравнением
,
подается стационарная с.ф.
с математическим ожиданием
и корреляционной функции
Найти
математическое ожидание и спектральную
плотность с.ф.
на выходе системы в установившемся
режиме.На вход линейной стационарной динамической системы, описываемой уравнением
,
подается стационарная с.ф.
с известной корреляционной функции
Найти
спектральную плотность с.ф.
на выходе системы в установившемся
режиме.На вход линейной стационарной динамической системы, описываемой уравнением
,
поступает с.ф.
с постоянной спектральной плотностью
(стационарный
белый шум). Найти дисперсию с.ф.
на выходе системы в установившемся
режиме.
Ответы
16.1.
|
Рост |
|
[155; 160) |
[160; 165) |
[165; 170) |
[170; 175) |
[175; 180) |
[180; 185) |
|
Число наблюдений |
|
3 |
5 |
7 |
7 |
5 |
3 |
|
Частота |
|
0,10 |
0,17 |
0,23 |
0,23 |
0,17 |
0,10 |
16.2.
2;1. 16.3.
0,226;0,004. 16.4.
.16.5.
.16.6.
.16.7. Опытные
данные согласуются с распределением
Пуассона на уровне значимости
.16.8. Нет
оснований при уровне значимости 0,01
отвергать предположение о нормальности
распределения с.в.
.16.9.
а)
;
б)
.16.10.
а)
;
б)
;
в)
.
16.11.
а)
;
б)
.16.12. а)
;
б)
;
в)
.
16.13.
.16.14. а)
;
б)
.16.15.
.16.16.
.
16.17.
а)
;
б)
.16.18. а)
Нет:
;
б) Нет: корреляционная функция зависит
не от разности аргументов, а от каждого
из них.16.19.
Да:
,
.16.20. Можно:
изменив начало отсчета аргумента,
например, на
,
стационарной функции
,
получим функцию
.16.21. а)
;
б)
,
.16.22.
.
16.23.
а)
;
б)
.
16.24.
.16.25.
.16.26.
.16.27.
.16.28.
.
16.29.
.
16.30.
а)
;
б)
;
в)
.16.31.
;
.
16.32.
;
.
16.33.
.16.34.
Для заметок
Для заметок
АГТУ Заказ ______ тираж ____ _____ __________ 2008г.