Случайные величины, их распределения и числовые характеристики Дискретные случайные величины

84. Пусть – число выпавших гербов при подбрасывании двух монет. Найти ряд распределения случайной величины.

85. В коробке 7 карандашей, из которых 4 – красные. Из этой коробки наудачу извлекаются 3 карандаша. Найти ряд распределения с.в. , равной числу красных карандашей в выборке.

86. Ряд распределения д.с.в. имеет вид:

	1	2	3	4	5
		0,15	0,30	0,25

Найти вероятности и, если известно, что.

84. Ряд распределения д.с.в. имеет вид:

	0	1	2	3
	0,2	0,4	0,3	0,1

Найти функцию распределения с.в. .

84. В партии из 10 деталей содержится 8 стандартных. Из этой партии наудачу взято 2 детали. Найти функцию распределения с.в. , равной числу стандартных деталей в выборке.

85. Ряд распределения д.с.в. имеет вид:

	-4	-2	0	2	4
	0,1	0,2	0,15	0,25	0,3

Записать законы распределения с.в. ии найти математические ожидания с.в.,,.

84. Подбрасывается игральный кубик. Найти математическое ожидание с.в. , равной числу выпавших очков.

85. Ряд распределения д.с.в. имеет вид:

	1	2	3	4	5
	0,05	0,15	0,30	0,40	0,10

Найти дисперсию и среднее квадратическое отклонениес.в..

84. Подбрасывается игральный кубик. Найти дисперсию и среднее квадратическое отклонение с.в. , равной числу выпавших очков.

85. Пусть – число выпавших решеток при трех подбрасываниях монеты. Найти числовые характеристики,ис.в..

86. Найти числовые характеристики ,ис.в., заданной рядом распределения

    	-0,1	0	0,1	0,4
    	0,30	0,15	0,30	0,25

87. Пусть ,,– все возможные значения д.с.в.и,. Найти ряд распределения с.в..

88. Д.с.в. может принимать только два значенияи, причем. Известны вероятность, математическое ожиданиеи дисперсия. Построить ряд распределения с.в..

Непрерывные случайные величины

84. Дана функция

Показать, что эта функция является функцией распределения некоторой с.в. . Найти.

84. Плотность вероятности с.в. задана функцией

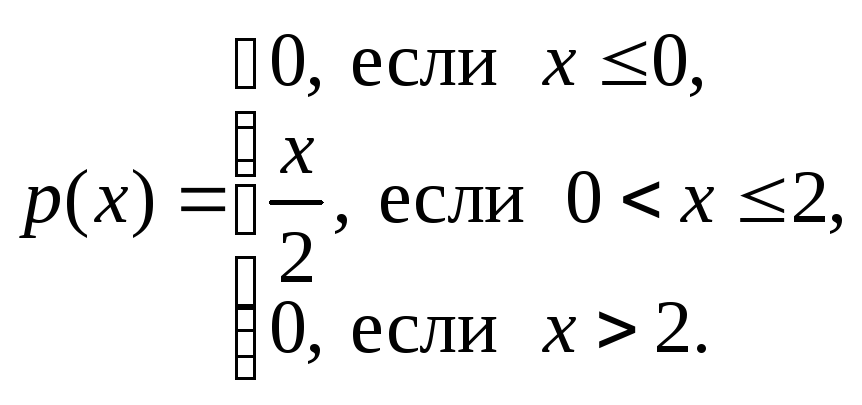
Найти вероятность .

84. Функция распределения с.в. имеет вид

Найти плотность вероятности с.в. .

84. Найти функцию распределения с.в. , плотность вероятности которой определена формулой

84. Дана функция

При каком значении постоянной функцияявляется плотностью вероятности некоторой с.в..

84. Функция распределения с.в. задана формулами

Найти значение коэффициента и плотность вероятности с.в.

84. Функция распределения с.в. имеет вид

Найти плотность вероятности с.в. и вероятность.

84. Плотность вероятности с.в. задана функцией

Найти математическое ожидание с.в. .

84. Найти математическое ожидание с.в. , если известна ее функция распределения

84. Найти математическое ожидание с.в. , если известна ее функция распределения

84. Найти числовые характеристики ,инепрерывной случайной величины, заданной плотностью вероятности

84. Непрерывная случайная величина задана плотностью вероятности

Найти числовые характеристики ,иэтой случайной величины.

84. Случайная величина задана функцией распределения

Найти числовые характеристики ,иэтой случайной величины.

84. Функция распределения с.в. имеет вид:

Найти ,,и.

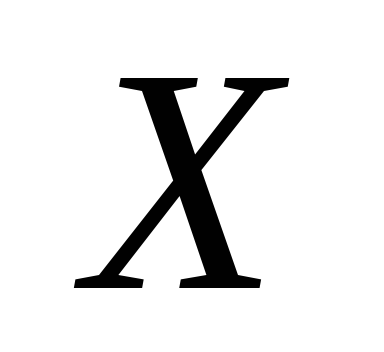84. С.в. распределена по нормальному закону с параметрам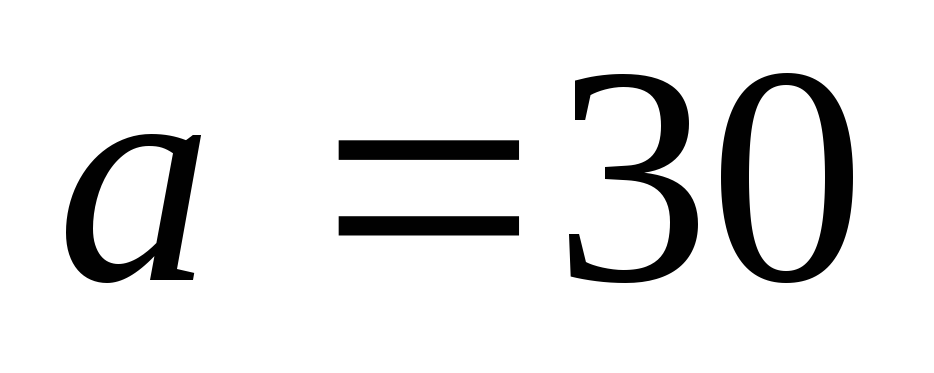ии. Найти вероятность того, что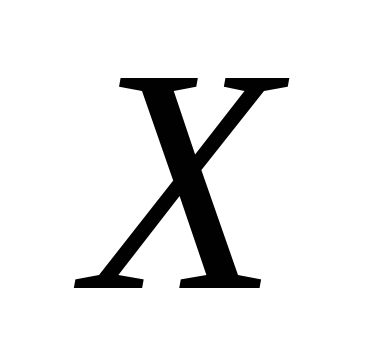примет значение, принадлежащее интервалу (10,50).

85. При изготовлении некоторого изделия его вес подвержен случайным колебаниям. Стандартный вес изделия равен 30г, его среднее квадратическое отклонение равно 0,7г, а с.в.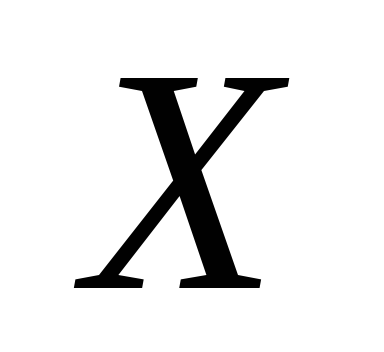распределена по нормальному закону. Найти вероятность того, что вес наугад выбранного изделия находится в пределах от 28г до 31г.

86. Среднее квадратическое отклонение с.в. , распределенной по нормаль-ному закону, равно 2 см, а математическое ожидание равно 16см. Найти границы, в которых с вероятностью 0,95 следует ожидать значение с.в..

87. Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами =375г,=25г. Найти вероятность того, что вес одной пойманной рыбы будет: а) от 300г до 425г; б) не более 450г; в) больше 300г.

88. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с параметром мм. Найти вероятность того, что измерение произведено с ошибкой, не превосходящей 15мм.

89. Станок-автомат изготавливает валики, контролируя их диаметры так, что с.в.распределена по нормальному закону с параметрамимм и, найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.

Ответы

15.2. в) A содержит 6 исходов, а B – 5. 15.3. нет. 15.4. нет. 15.5. а) ; б); в); г).15.6. Только в).

15.8. а) ; б); в); г); д); е); ж); з).15.9. 20. 15.10. 20. 15.11. 49 и 42. 15.12. 60. 15.13. 7!=5040. 15.14. =151200.15.15. =495.15.16. 60 и 10. 15.17. 18000. 15.18. 60. 15.19. 120 и 60. 15.20. (n-2)! 15.21. 65=7776. 15.22. 283104. 15.23. (5!)2=14400.

15.24. (n!)2. 15.25. 2(7!)2=50803200. 15.26. 3(5!)2=43200.

15.27. 10!/24=151200. 15.28. .15.29. а) 210; б) 420.

15.30. /10⁵=0,3024. 15.31. 2/91. 15.32. 3/38. 15.33. 1/10.

15.34. 32/33. 15.35. 2/3. 15.36. 3/5. 15.37. 1/20. 16.38. 11!/1211.

15.39. 1/2. 15.40. 1/216. 15.41. 1/6. 15.42. 2/15. 15.43. 0,09.

15.44. 1/216, 1/36, 5/54. 15.45. 0,7. 15.46. 1/4. 15.47. 1/3. 15.48. 1/2. 15.49. 2/π. 15.50. π/4. 15.51. 3/4. 15.52. 3/4. 15.53. 1/12.

15.54. 2(r/R)2. 15.55. 2/3 и 1/3. 15.56. 40/49. 15.57. зависимы.

15.58. 15/16. 15.59. 7/9. 15.60. 0,94, 0,95 и 0,93. 15.61. 5/21.

15.62. 0,7. 15.63. 5/9. 15.64. 1/720. 15.65. 0,0256. 15.66. а) 0,1296; б) 0,0256; в) 0,9744. 15.67. 1) 0,30; 2) 0,45; 3) 0,35; 4) 0,50; 5) 0,50.

15.68. 0,68. 15.69. 4/15. 15.70. 0,23. 15.71. 51/90. 15.72. 2.

15.73. 13/30. 15.74. 0,022. 15.75. 0,9935. 15.76. 0,87. 15.77. 0,292. 15.78. 0,5. 15.79. 0,345. 15.80. 9/16 и 1/21. 15.81. 20/21.

15.82. 0,2787. 15.83. 3 из 4. 15.84. 3/16. 15.85. 0,3723.

15.86. 0,73728. 15.87. 0,0916. 15.88. 0,918. 15.89. 21/32 и 1023/1024. 15.90. 0,1562. 15.91. а) 0,06313; б) 0,367879; в) 0,981011; г) 0,018989. 15.92. а) 0,577; б) 0,1992; в) 0,224; г) 0,95. 15.93. а) 0,00146; б) 0,0236. 15.94. 55. 15.95. 0,6961. 15.96. 0,7698.

15.97. 0,9736. 15.98. 0,0034.

15.99. 0 1 2 0,25 0,50 0,25	15.100. 0 1 2 3 1/35 12/35 18/35 4/35 .
15.101. и.
15.102.	15.103.
15.104. -12 -6 0 6 12 ; -2 -1 0 1 2 ; 0,1 0,2 0,15 0,25 0,3 0,1 0,2 0,15 0,25 0,3

15.105. 3,5. 15.106. 1,0275. 15.107. 2,917 и 1,708. 15.108. 1,5; 0,75; 0,866. 15.109. 0,1; 0,036; 0,190.

15.110. 1 2 3 0,2 0,3 0,5 .

15.111. 3 4 0,5 0,5 .

15.112. 0,5. 15.113. 0,75.