Формула полной вероятности и формула Байеса

15.73. Имеются два одинаковых ящика с шарами. В первом ящике 2 белых и 1 чёрный шар, во втором – 1 белый и 4 чёрных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется белым?

74. На фабрике, изготовляющей болты, первая машина производит 30%, вторая – 25%, третья – 45% всех изделий. Брак в их продукции составляет соответственно 2%, 1%, 3%. Найти вероятность того, что случайно выбранный болт оказался дефектным.

75. Партия электрических лампочек на 20% изготовлена первым заводом, на 30% – вторым, на 50% – третьим. Вероятности выпуска бракованных лампочек соответственно равны 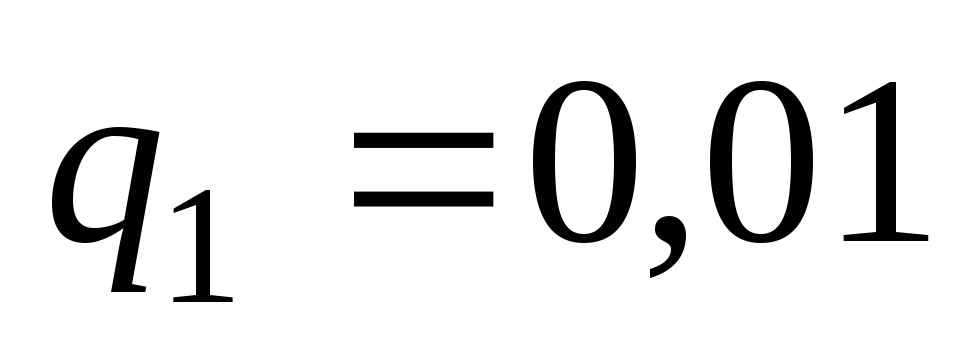,,. Найти вероятность того, что наудачу взятая из партии лампочка окажется стандартной.

76. На двух автоматических станках изготовляются одинаковые детали. Известно, что производительность первого станка в два раза больше, чем второго, и что вероятность изготовления детали высшего качества на первом станке равна 0,9, а на втором – 0,81. Изготовленные за смену на обоих станках нерассортированные детали находятся на складе. Найти вероятность того, что наудачу взятая деталь окажется высшего качества.

77. Имеются три урны с шарами. В первой находится 5 синих и 3 красных шара, во второй – 4 синих и 4 красных, в третьей – 8 синих. Наугад выбирается одна из урн и из неё наугад извлекается шар. Какова вероятность того, что он окажется красным?

78. В ящике находятся одинаковые изделия, изготовленные на двух автоматах: 40% изделий изготовлено первым автоматом, остальные – вторым. Брак в продукции первого автомата составляет 3%, второго – 2%. Найти вероятность того, что случайно выбранное изделие изготовлено первым автоматом, если оно оказалось бракованным.

79. Партия деталей изготовлена тремя рабочими, причём первый изготовил 35% всех деталей, второй – 40%, третий – всю остальную продукцию. Брак в их продукции составляет: у первого – 2%, у второго – 3%, у третьего – 4%. Случайно выбранная для контроля деталь оказалась бракованной. Найти вероятность того, что она изготовлена третьим рабочим.

80. В первой урне 2 белых и 6 красных шаров, во второй – 4 белых и 2 красных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали 1 шар. Какова вероятность того, что этот шар – белый?

Предположим, что шар, взятый из второй урны, оказался белым. Какова вероятность того, что из первой урны во вторую были переложены 2 белых шара?

74. Известно, что 5% всех мужчин и 0,25% всех женщин – дальтоники. Наудачу выбранное лицо оказалось дальтоником. Какова вероятность того, что это – мужчина? Считать, что мужчин и женщин – одинаковое число.

Испытания Бернулли. Формулы Пуассона и Муавра-Лапласа.

74. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?

15.83. Что вероятнее – выиграть у равносильного противники 3 партии из 4 или 5 партий из 8 (ничейный исход партии исключен)?

84. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди пяти случайно выбранных волокон смеси обнаружить менее двух окрашенных?

85. Вероятность рождения мальчика равна 0,515, девочки – 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

86. Всхожесть семян некоторого сорта растений оценивается вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырёх?

87. Вероятность того, что любой из 800 абонентов телефонной станции позвонит на коммутатор в течение часа, равна 0,01. Какова вероятность того, что в течение часа позвонят 5 абонентов.

88. Применяемый метод лечения приводит к выздоровлению в 90% случаев. Какова вероятность того, что из 5 больных поправятся не менее 4?

89. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.

90. Вероятность изготовления нестандартной детали 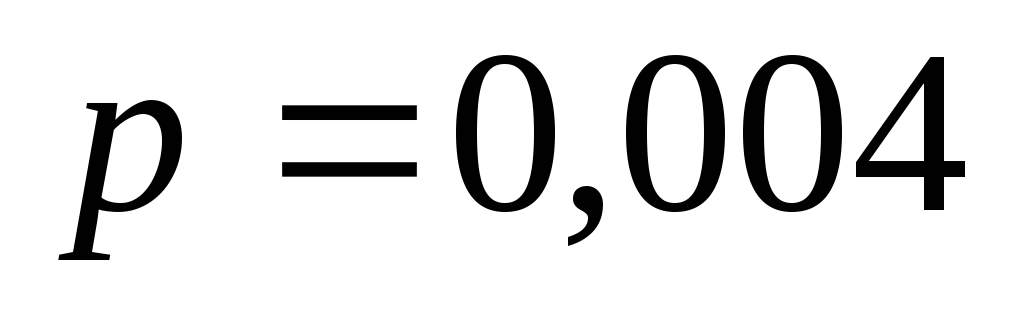. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.

91. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что среди 5000 изделий в пути будет повреждено: а) ровно 3 изделия; б) ровно 1 изделие; в) не более 3 изделий; г) более 3 изделий.

92. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что бутылка при перевозке окажется разбитой, равна 0,003. Найти вероятность того, что среди полученных бутылок разбитых будет: а) более двух; б) менее двух; в) ровно две; г) хотя бы одна.

93. Вероятность появления события в каждом из 900 независимых испытаний равна. Найти вероятность того, что событиепроизойдет: а) 750 раз; б) 710 раз.

94. Сколько раз с вероятностью 0,0484 можно ожидать появление события в 100 независимых испытаниях, если вероятность его появления в отдельном испытании равна 0,5.

95. Вероятность приема каждого из 100 передаваемых сигналов равна 0,75. Найти вероятность того, что будет принято от 71 до 80 сигналов.

96. Вероятность появления события в каждом из 900 независимых испытаний равна. Найти вероятность того, что частота появления событияотклонится от его вероятности по модулю не больше, чем на 0,02.

97. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших заключено между 790 и 830.

98. Посажено 600 семян кукурузы с вероятностью 0,9 прорастания для каждого семени. Найти границу модуля отклонения частоты взошедших семян от вероятности , если эта граница должна быть гарантирована с вероятностью.