15. Теория вероятностей Случайные события и их вероятности Классификация событий. Операции над событиями

15.1. Монета подбрасывается три раза подряд. Под исходом опыта будем понимать упорядоченный набор , где каждый изобозначает выпадение герба или решетки. Нужно: а) построить пространство элементарных событийдля нашего опыта и б) описать событие– “выпало не менее двух гербов”.

15.2. Подбрасываются два игральных кубика (номер 1 и номер 2). Под исходом опыта будем понимать упорядоченную пару , где каждый из(результат для-го кубика) обозначает выпадение одного, двух,…, пяти и шести очков. Требуется: а) построить пространство элементарных событийдля нашего опыта, б) описать событие– “на обоих кубиках выпало одинаковое число очков” и в) выяснить, какое событие содержит больше элементарных событий:– “сумма выпавших очков равна 7” или– “сумма выпавших очков равна 8”.

3. Производят два выстрела по мишени. Выяснить, являются ли несовместными следующие два события: – “наличие хотя бы одного попадания” и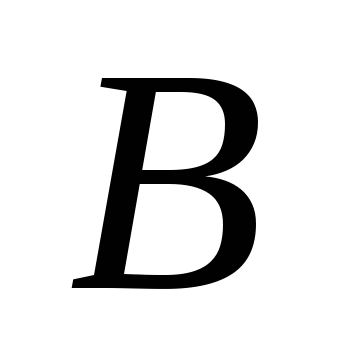– “наличие хотя бы одного промаха”.

4. Опыт заключается в подбрасывании двух монет. Образуют ли полную группу несовместных событий следующие два события: – “выпадение двух гербов” и– “выпадение двух решеток”?

5. Упростите следующие выражения: а);

б) ; в); г).

3. Установить какие из следующих соотношений правильны: а); б); в); г).

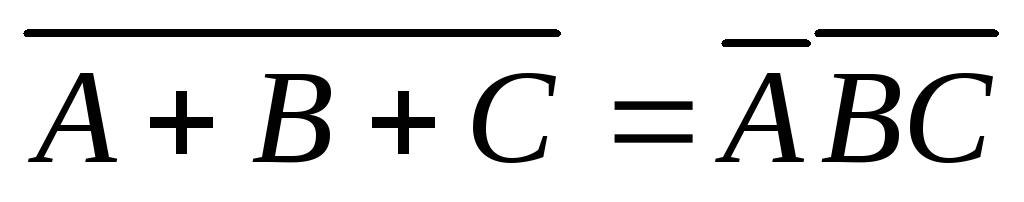4. Доказать, что события ,иобразуют полную группу несовместных событий.

5. Пусть ,,и– три произвольных события. Найти выражения для событий, которые состоятся в следующих случаях: а) произошло только событие; б) произошло одно и только одно событие; в) произошли два и только два события; г) все три события произошли; д) произошло по крайней мере одно событие; е) произошло не более двух событий; ж) произошли по крайней мере два события; з) ни одно событие не произошло.

Элементы комбинаторики

15.9. Имеется 5 видов конвертов без марок и 4 вида марок одного достоинства. Сколькими способами можно приготовить конверт с маркой указанного достоинства?

10. Сколько словарей нужно издать, чтобы переводить с любого из пяти языков на любой другой из этих языков?

11. На вершину горы ведет 7 дорог. Сколькими способами турист может подняться на гору и спуститься с неё? Дайте ответ на тот же самый вопрос, если подъем и спуск осуществляются разными дорогами.

12. Сколько трехзначных чисел можно составить из цифр 1,2,3,4,5, если каждую из этих цифр можно использовать не более одного раза?

13. Сколькими способами 7 человек могут разместиться в очереди в кассу?

14. В классе изучают 10 предметов. В понедельник – 6 уроков, причем все уроки – разные. Сколькими способами можно составить расписание на понедельник?

15. В классе 12 ламп. Сколько всего разных способов освещения класса, при которых горит ровно 8 ламп?

16. Группе из пяти сотрудников выделено три путевки. Сколько существует способов распределения путевок, если: а) все путевки разные; б) все путевки одинаковые?

17. Сколько имеется пятизначных чисел, делящихся на 5?

18. Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать их обратно, выяснилось, что он забыл номер. Он только помнил, что в номере были числа 23 и 57. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру?

19. а) Сколькими способами можно составить трехцветный полосатый флаг (с горизонтальными полосами), если имеется материал 6 различных цветов? б) Та же задача, если одна из полос должна быть красной.

20. Сколькими способами можно упорядочить множество так, чтобы числа 1,2,3 стояли рядом и в порядке возрастания?

21. Кодовое устройство пятиразрядного цифрового замка состоит из пяти вращающихся дисков, каждый из которых имеет 6 цифр от 0 до 5. Только одна из комбинаций позволяет открыть замок. Сколько всего комбинаций?

22. Автомобильный номер состоит из трех букв и четырех цифр. Найти число таких номеров, если использовать 28 букв алфавита.

23. 5 мальчиков и 5 девочек садятся в ряд на 10 расположенных подряд стульев, причем мальчики садятся на места с нечетными номерами, а девочки – на места с четными номерами. Сколькими способами это можно осуществить?

24. Сколькими способами можно упорядочить множество так, чтобы каждое четное число имело четный номер?

25. Сколькими способами можно посадить за круглый стол 7 юношей и 7 девушек так, чтобы никакие две девушки не сидели рядом?

26. В купе ж/д вагона имеется два противоположных дивана по 5 мест в каждом. Из 10 пассажиров четверо желают сидеть лицом к паровозу, а трое – спиной к нему; остальным трем безразлично, как сидеть. Сколькими способами могут разместиться пассажиры?

27. Сколько разных слов (считая и абсолютно бессмысленные) можно составить перестановкой букв в слове “математика”?

28. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях 64-клеточной шашечной доски?

29. Сколько разных слов (включая и абсолютно бессмысленные) можно составить: а) из букв слова “колокол”; б) из букв слова “водород”, используя все буквы слова?