14. Функции комплексной переменной

и преобразование Лапласа

Комплексные числа и действия над ними

Представить в алгебраической форме:

14.1. .	14.2. .	14.3. .
14.4. .	14.5. .	14.6. .
14.7. .	14.8. .	14.9. .
14.10. .	14.11. .

14.12.

14.13.

Представить в тригонометрической и показательной форме комплексные числа:

14.14. 1.	14.15. –1.	14.16. .
14.17. .	14.18. .	14.19. .
14.20. .	14.21. .	14.22. .
14.23. .	14.24. .	14.25. .
14.26. .

Найти все значения корней:

14.27. .	14.28. .	14.29. .
14.30. .	14.31. .	14.32. .

Решить уравнения:

14.33. .	14.34. .	14.35. .
14.36. .

Вычислить:

14.37. .	14.38. .
14.39. .	14.40. .
14.41. .

Найти пределы числовых последовательностей

14.42.	.
14.43.	.
14.44.	.
14.45.	.
14.46.	.
14.47.	.
14.48.	.
14.49.	.

Найти множества точек на плоскости, которые определяются заданными условиями:

14.50. .	14.51. .	14.52. .
14.53. .	14.54. .	14.55. .

Указать какие линии определяются следующими уравнениями

14.56. .	14.57. .	14.58. .
14.59. .	14.60. .	14.61. .
14.62. .	14.63. .	14.64. .

14.65. .

Функции комплексного переменного

66. Найти действительную и мнимую части следующих переменных:

    а) 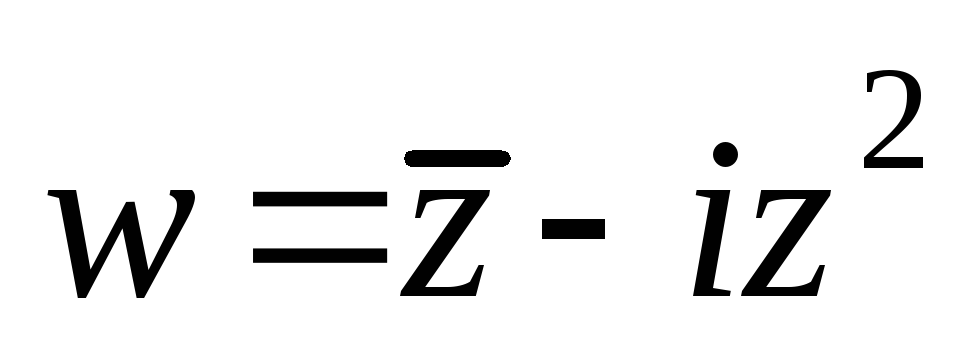;	б) ;	в) ;
    г) ;	д) ;	е) .

67. Найти образ точки при отображении:

    а) ,;	б) ,;
    в) ,;	г) ,.

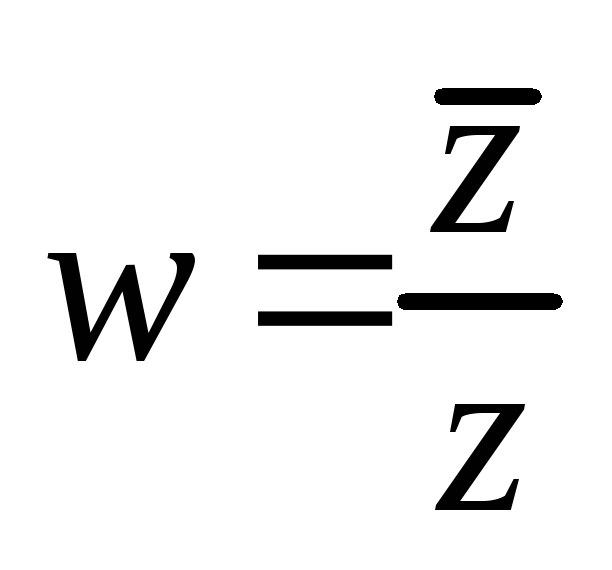68. Выделить действительную и мнимую части у следующих функций:

    а) ;	б) ;	в) ;	г) ;
    д) ;	е) ;	ж) .

69. Доказать тождества:

    а) ;

    б) ;

    В) .

70. Записать в алгебраической форме:

    а) 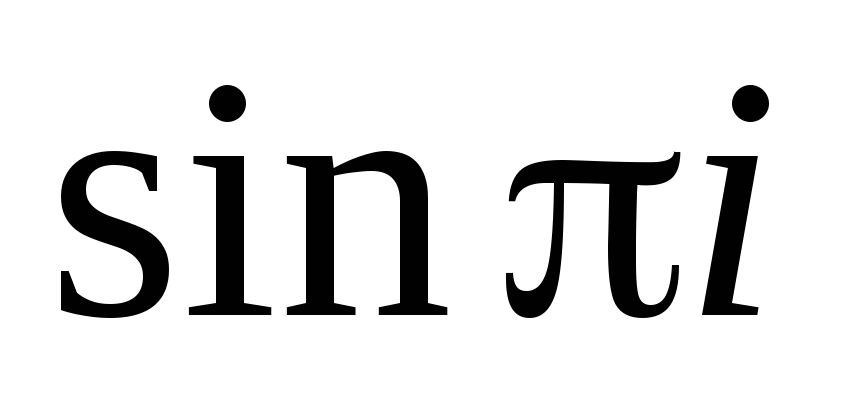;	б) ;	в) ;	г) ;	д) ;
    е);	ж) ;	з) ;	и) .

71. Записать в алгебраической форме:

    а) Lne;	б) Ln(–i);	в) Lni;
    г) ;	д) ;	е) .

72. Вычислить:

    а) ;	б) ;	в) ;	г) ;
    д) ;	е) ;	ж) .

73. Решить уравнение.

а) ;	б) ;	в) ;
г) ;	д) х– действительное;	е) ;
ж) ;	з) ;	и) .