Задачник по линейной Алгебре и Мат Анализу / Часть 13
.doc13. Основные задачи и уравнения
математической физики
Простейшие дифференциальные уравнения
в частных производных
-
Найти функцию
,
удовлетворяющую дифференциальному
уравнению
. -
Найти функцию
,
удовлетворяющую дифференциальному
уравнению
. -
Решить дифференциальное уравнение
. -
Решить дифференциальное уравнение
. -
Решить дифференциальное уравнение
.
Определить тип уравнений и привести
их к каноническому виду
-
-
-
-
-
-
.
-
. -
. -
. -
. -
. -
.
Отыскание общего решения указанного уравнения
-
. -
. -
. -
. -
.
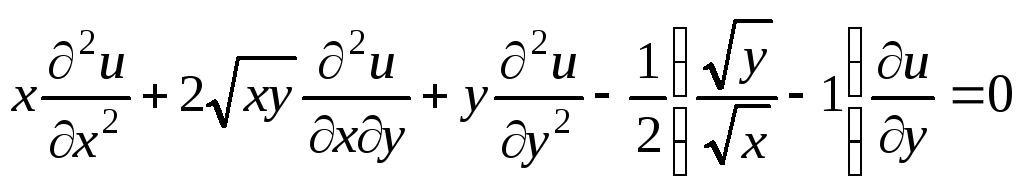Аналитические методы решения
уравнений математической физики
Метод Даламбера
-
Найти решение уравнения
при начальных условиях
. -
Найти решение уравнения
при начальных условиях
. -
Найти решение уравнения
при начальных условиях
,
. -
Найти решение уравнения
при начальных условиях
,
. -
Найти решение уравнения
при начальных условиях
,
.
Метод Фурье
-
Найти отклонение u(x,t) от положения равновесия закрепленной на концах x=0 и x=l однородной горизонтальной струны, если в начальный момент струна имела форму
,
а начальные скорости отсутствовали. -
Найти отклонение u(x,t) от положения равновесия закрепленной на концах x=0 и x=l однородной горизонтальной струны, если в начальный момент точки струны находились в положении равновесия и ей была придана начальная скорость
. -
Найти отклонение u(x,t) от положения равновесия закрепленной на конце x=l однородной горизонтальной струны, левый конец которой при x=0 перемещается так, что касательная к струне остается горизонтальной, если в начальный момент струна имела форму
,
а начальная скорость отсутствовала. -
Найти отклонение u(x,t) закрепленной на концах x=0 и x=l однородной горизонтальной струны от положения равновесия, если в начальный момент струна имела форму параболы с вершиной в точке x=l/2 и отклонением от положения равновесия h, а начальные скорости отсутствовали.
-
Найти колебания закрепленной на концах x=0 и x=l однородной горизонтальной струны, находящейся в положении равновесия, если в начальный момент времени ударом молоточка в точке x=l/3 ей сообщается постоянная начальная скорость,
где /h
– ширина молоточка. -
Найти закон свободных колебаний закрепленной на конце x=0 однородной струны, если правый ее конец при x=l перемещается так, что касательная к струне остается постоянно горизонтальной. В начальный момент струна находилась в положении равновесия и ей была придана начальная скорость ut(x,0)=sin
.
-
Закрепленной в точке x=l однородной горизонтальной струне, левый конец которой в точке x=0 может перемещаться с горизонтальной касательной, придана начальная скорость
.
Найти закон ее свободных колебаний,
если в начальный момент она имела форму
. -
Найти решение уравнения:
,
,
удовлетворяющее условиям
-
Дан тонкий однородный стержень длиной l, изолированный от внешнего пространства, начальная температура которого равна
Концы стержня поддерживаются при температуре, равной нулю. Определить температуру стержня в момент времени t (t>0).
13.37. Растворенное
вещество с начальной концентрацией
диффундирует из раствора, заключенного
между плоскостями x=0
и x=h,
в растворитель, ограниченный плоскостями
x=h
и x=l.
Определить процесс выравнивания
концентраций, предполагая, что границы
x=0 и x=l
непроницаемы для вещества.
Ответы
13.1.
.
13.2.
.
13.3.
.
13.4.
.
13.5.
.
13.6.
Гиперболический,
(
и
).
13.7.
Эллиптический,
(
и
).
13.8.
Параболический,
(
и
).
13.9.
Эллиптический,
(
и
).
13.10.
Параболический,
(
и
).
13.11.
Гиперболический,
.
13.12.
Эллиптический. Выбирая
и
,
после преобразования получаем уравнение
.
13.13. В
области D{(x,y)|x0,
y0}
эллиптический,
.
При x=0
или y=0
параболический.
13.14.
Параболический. Выбирая
и
,
после преобразования получаем уравнение
.
13.15.
В области
гиперболический,
.
При
или
параболический. 13.16.
Гиперболический,
.
13.17.
В области
гиперболический
.
При
параболический.13.18.
,
где
произвольные дважды дифференцируемые
функции. 13.19.
,
где
– произвольные дважды дифференцируемые
функции. 13.20.
,
где
– произвольные дважды дифференцируемые
функции. 13.21.
,
где
– произвольные дважды дифференцируемые
функции. 13.22.
,
где
– произвольные дважды дифференцируемые
функции. 13.23.
.
13.24.
.
13.25.
.
13.26.
13.27.
.
13.28.
.
13.29.
.
13.30.
.
13.31.
.
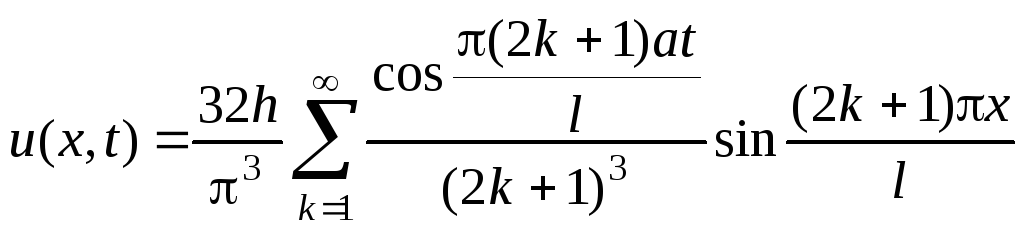13.32.
.
13.33.
13.34.
.
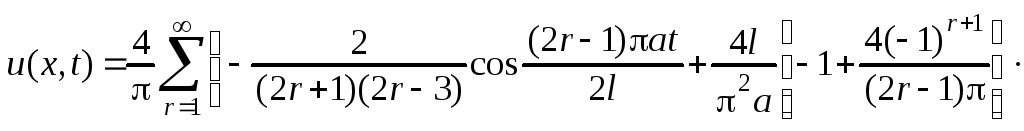
13.35.
13.36.
13.37.
(Воспользоваться уравнением
с соответствующими краевыми и начальными
условиями).