Производные и дифференциалы высших порядков

Найдите производные 2^гопорядка от следующих функций:

5.266. y=x8+7x6–5x+4.	5.267. y =.
5.268. y=sin2x.	5.269. y = .
5.270. y=.	5.271. f(x)=(1+x2)arctgx.
5.272. y=(arcsinx)2.	5.273. y =.
5.274. y =.	5.275. y =
5.276. y =.
5.277. y =.	5.278. y =.
5.279. y =.	5.280. y =.
5.281. y =.	5.282.y =.
5.283.y =arcsin(asinx).	5.284.y =xx.

Найти производные 3^гопорядка от следующих функций:

5.285.y =	5.286. y =
5.287. y =sh2x	5.288.y =

5.289.Показать, что функцияy=sin(lnx)+cos(lnx) удовлетворяет

дифференциальному уравнению .

5.290.Показать, что функцияy=x+sin2xудовлетворяет дифференциальному уравнению.

5.291.Показать, что функцияy=arcsinxудовлетворяет дифференциальному уравнению.

5.292.При прямолинейном движении точки зависимость пути от времени задана уравнением. Найти ускорение в конце 4^ойсекунды.

5.293. Показать, что функцияy=с₁e^2x+c₂xe^2x+e^xудовлетворяет дифференциальному уравнению.

5.294.Показать, что функцияy=e^–xcosxудовлетворяет дифференциальному уравнению.

Найдите производные 2^го порядка от функций, заданных неявно:

5.295..	5.296.y2=2px.
5.297. y=xey+1.	5.298. y=tg(x+y).
5.299. ex–y=xy.

5.300.Доказать, что если, то.

Найдите производные 2^гопорядка следующих функций, заданных параметрически:

5.301..	5.302..
5.303..	5.304..
5.305..

5.306.Показать, что функцияy(x), заданная параметрически уравнениямиx=sint,y=при любых постоянныхаиbудовлетворяет дифференциальному уравнению (1–x²).

5.307.Показать, что функцияy(x), заданная параметрически уравнениямиy=e^tcost,x=e^tsintудовлетворяет дифференциальному уравнению(x+y)²=2(xy–y).

Найдите n-ю производную от функций:

5.308. y=e–3x.	5.309. y=sinax+cosbx.	5.310. y=sin2x
5.311. y=xex.	5.312. y=2x.	5.313. y=
5.314. y=.	5.315. y=ln(ax+b).	5.316. y=
5.317. y=.	5.318. y=.	5.319. y=sin4x+cos4x
5.320. y=.

5.321.Найдите, если.

5.322.Вычислитеd²y, еслиy=cos5x.

5.323.y=, найдитеd ²y.

5.324.y=arccosx, найдитеd ²y.

5.325.y=sinxlnx, найдитеd ²y.

5.326.найдитеd ⁴y.

5.327.z=x²e^–x, найтиd ³z.

5.328.u=3sin(2x+5), найдитеd ⁿu.

Теоремы о дифференцируемых функциях. Формула Тейлора

329. Можно ли на отрезке [–1;1] применить к функции f(x)=a) теорему Ролля, б) теорему Лагранжа о конечных приращениях?

330. Применима ли теореме Ролля к функции f(x)=на отрезке [0;1]? В каких точкахf(x)=0?

331. Показать, что функция f(x)=x–x³на отрезках –1x0 и 0x1 удовлетворяет условиям теоремы Ролля. Найти соответствующие значения.

332. Функция f(x)=на концах отрезка [0;4] принимает равные значенияf(0)=f(4)=. Справедлива ли для этой функции теорема Ролля на отрезке [0;4].

333. Справедлива ли для функции теорема Ролля на [–1;1]?

334. Пусть f(x)=x(x+1)(x+2)(x+3). Показать, что уравнениеf(x)=0 имеет три действительных корня.

335. Показать, что уравнение х³+3х–6=0 имеет только один действительный корень.

336. Не находя производную функции f(x)=(x–1)(x–2)(x–3)(x–4), выяснить, сколько действительных корней имеет уравнениеf(x)=0 и указать интервалы, в которых они лежат.

337. Написать формулу Лагранжа для функции y=sin3xна отрезке [x₁;x₂].

338. Написать формулу Лагранжа для функции y=x(1–lnx) на отрезке [a;b].

339. Написать формулу Лагранжа для функции y=arcsin2xна отрезке [x₀;x₀+x].

340. Проверить выполнение условий теоремы Лагранжа для функции f(x)=x–x³на отрезке [–2;1] и найти соответствующее промежуточное значение.

341. Проверить выполнение условий теоремы Лагранжа и найти соответствующую промежуточную точку для функцииf(x)=на [–1;1].

342. Для отрезка параболы y=x², заключенного между точкамиА(1;1) иВ(3;9), найти точку, касательная в которой параллельна хордеAВ.

343. Пользуясь теоремой Лагранжа доказать формулу sin(x+h)– –sinx=hcos, гдеx<<x+h.

344. Доказать с помощью формулы Лагранжа неравенства

при условии, что 0<ba.

329. Доказать с помощью формулы Лагранжа неравенства

при условии, что.

329. Используя формулу Лагранжа оценить значение ln(1+).

330. Используя формулу Лагранжа оценить значение arctg1,5.

331. a) Для функцийf(x)=x²+2 иF(x)=x³–1 проверить выполнение условий теоремы Коши на отрезке [1;2] и найти; б) то же дляf(x)=sinxиF(x)=cosxна отрезке

332. Применима ли теорема Коши к функциям f(x)=cosxиF(x)=x³на отрезке

333. Доказать, что на отрезке (х0) приращение функцииy₁=ln(1+x²) меньше приращения функцииy₂=arctgx, а на отрезкенаоборот. Пользуясь последним соотношением, показать, что на отрезке arctgx–ln(1+x²)–ln2.

334. Разложить многочлен P(x)=2x⁴–5x³–3x²+8x+4 по степеням х–2.

335. Написать формулу Тейлора n^гопорядка для функцииy =приx₀= –1.

336. Написать формулу Маклорена n^гопорядка для функцииy=xе^х.

337. Написать формулу Тейлора n^гопорядка для функцииy=приx₀=4.

338. Оценить ошибку, которую мы допускали, вычисляя значение ln1,5 по приближенной формулеln(1+x)x–т.е. используя четыре первых члена разложения функцииf(x)=ln(1+x) в ряд Маклорена.

339. Используя разложение f(x)=sinxв ряд Маклорена, оценить абсолютную погрешность приближенной формулыsinxx–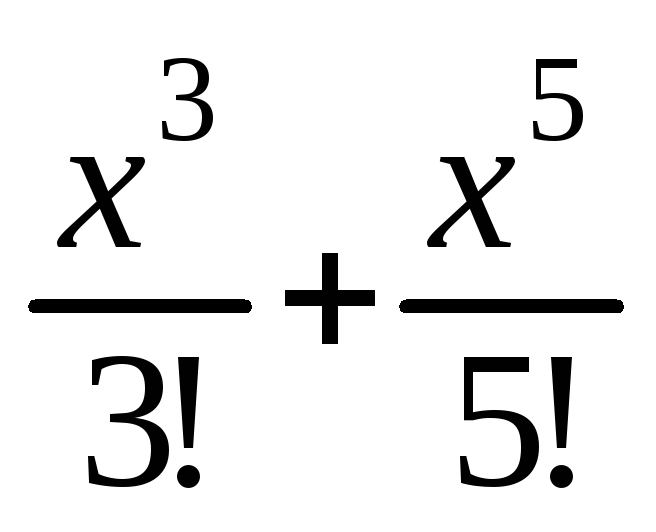на промежутке.

340. Используя разложение функции f(x)=ln(1+x) в ряд Маклорена, оценить погрешность приближенной формулыln(1+x)x–на отрезке.

341. Пользуясь приближенной формулой e^x1+x+, найдитеи оцените погрешность.

342. Вычислить число ес абсолютной погрешностью, не превосходящей 0,001.

Найдите пределы используя правило Лопиталя.

5.360..	5.361..
5.362..	5.363..
5.364..	5.365..
5.366..	5.367..
5.368..	5.3691..
5.370..	5.371..
5.372..	5.373..
5.374..	5.375..
5.376..	5.377..
5.378..	5.379..
5.380..	5.381..
5.382..	5.383..
5.384..	5.385..
5.386..	5.387..
5.388..