5. Дифференциальное исчисление функции

Одной переменной и его приложения

Производная, ее геометрический и физический смысл

Правила и формулы дифференцирования

исходя из определения производной (не пользуясь формулами дифференцирования), найти производные следующих функций:

5.1 y = 5x3+3x2–4x+1	5.2. y =	5.3. y =–ctgx–x
5.4. y=1/x2	5.5. y =	5.6. y=5sinx+3cosx
5.7. y =5(tgx–x)	5.8. y =1/(ex+1)	5.9. y =

Найти производные следующих функций:

5.10. y =x5–4x3+2x–3.		5.11. y =.
5.12. y =.		5.13. y =.
5.14. y =.		5.15. y =.
5.16. y =.		5.17. y = x7ex.
5.18. y = (x–1)ex.		5.19. y =.
5.20. y =.		5.21. f(x) = excosx.
5.22. y = (x2–2x+2)ex.		5.23. y =exarcsinx.
5.24. y =.		5.25. y =x3lnx–.
5.26. y =.		5.27. y =lnxlgx–lna.
5.28. y =xshx.		5.29. y =.
5.30. y =thx–x.	5.31. y =.
5.32. y =arctgx–Arthx.	5.33. y =arcsinxarshx.
5.34. y =.	5.35. y =.
5.36. y =.	5.37. y =atg.
5.38. y =.	5.39. y=arctg(x2–3x+2).
5.40. y =lg(x–cosx).	5.41. y =3cos2x–cos3x.
5.42. y =5tg.	5.43. y =.
5.44. y =sinsin2x.	5.45. y =sinxecosx.
5.46. y =.	5.47. y = .
5.48. y =.	5.49. y =arctg.
5.50. y =.	5.51. y =.
5.52. y =.	5.53. y =.
5.54. y =.	5.55. y =.
5.56. y =.	5.57. y =xarctg.
5.58. y =.	5.59. y =cos2xlnx.
5.60. y =arctgx+arctg.	5.61. y =arcsin(nsinx).
5.62. y =arcsin.	5.63. y =sin6(3x)–sin83x.
5.64. y =x–arcsinx.	5.65. y =cos.
5.66. y =.			5.67. y =arccos.
5.68. y =sin2.			5.69. y =log3(x2–sinx).
5.70. y =arctg.			5.71. y =ln.
5.72. y =xarcsin(lnx).			5.73. y =tg.
5.74. y =cosx.			5.75. y =0,4.
5.76. y =.			5.77. y =.
5.78. y =lnarctg.			5.79. y =ln.
5.80. y=.			5.81. y =x2.
5.82. y =.			5.83. y =x3arctgx3.
5.84. y =.			5.85. y =arcsinx+.
5.86. y =.			5.87. y = .
5.88. y =.			5.89. y =10xtgx.
5.90. y =sin2xsinx2.			5.91. y =.
5.92. y =.			5.93. y =.
5.94. y =.			5.95. y =.
5.96. y =.			5.97. y =.
5.98.y =aarccos.			5.99. y =.
5.100. y =.			5.101. y =.
5.102. y = eax(asinx–cosx).			5.103. y = xe1–cosx.
5.104. y =.			5.105. y = ex(sin3x–3cos3x).
5.106. y=3x3arcsinx+(x2+2).			5.107. y =.
5.108. y=2arcsin.			5.109. y = ln(excosx+e–xsinx).
5.110. y =.			5.111. y =.
5.112. y =exsinxcos3x.			5.113. y =.
5.114.y=x–ln			5.115. y =.
5.116. y =.			5.117.y=–ctgxln(1+sinx)–x.
5.118. y=2ln– -6arcsin2x			5.119. y =+arctgx.
5.120.y =(3–x)+ +2arcsin.			5.121. y = sh32x.
5.122. y =.			5.123. y = th32x.
5.124. y = lnsh2x.			5.125. y = Arsh.
5.126. y = Archlnx.			5.127. y =Arth(tgx).
5.128. y =Arcth(secx).			5.129. y =Arth
5.130. y =

Найти частные значения производных:

5.131.y=приx=0; 1;

5.132.y=arcsinприx=1;

5.133.y=приx=3.

5.134.y=e^xsinприx=0.

5.135.y=приx=0.

5.136.Доказать, что функцияy=xsinxудовлетворяет уравнению

.

5.137.Доказать, что функцияy=3+(5/x) удовлетворяет уравнениюxy+y=3.

5.138.Доказать, что функцияy=(х+1)е^х удовлетворяет уравнениюy–y=е^х.

5.139.Доказать, что функцияy=при любом постоянном значенииСудовлетворяет уравнениюxуy=1–х².

5.140.Доказать, что функцияy=удовлетворяет уравнению

xy=(1–х²)у.

5.141.Найти угловой коэффициент касательной, проведенной к параболеу=х²: 1) в начале координат, 2) в точке (3;9), 3) в точке (–2;4), 4) в точках пересечения ее с прямойу=3х–2.

5.142.В каких точках угловой коэффициент касательной к кубической параболеу=х³равен 3?

5.143В какой точке касательная к параболеу=х³: 1) параллельна осиОХ, 2) образует с осьюOXугол в 45⁰?

5.144.Может ли касательная к кубической параболеу=х³составить с осьюОХтупой угол.

5.145.Под какими углами пересекаются параболау=х²и прямая 3х–у–2=0?

5.146.Под какими углами пересекаются параболыу=х²иу²=x?

5.147.Под каким углом пересекается гиперболау=1/xс параболойу=

5.148.Написать уравнения касательной и нормали, проведенных к кривойу=х³в точке с абсциссой 2. Найти подкасательную и поднормаль.

5.149.При каком значениихкасательные к кривыму=х²иу=х³параллельны?

5.150. В какой точке касательная к параболеу=х²: 1) параллельна прямойу=4х–5; 2) перпендикулярна к прямой 2х–6у+5=0; 3) образует с прямой 3х–у+1=0 угол в 45⁰?

5.151.Точка движется по прямой так, что ее расстояниеSот начального пункта черезtсек равноS=(1/4)t⁴–4t³+16t².

а) в какие моменты точка была в начальном пункте? б) в какие моменты ее скорость равна нулю?

5.152.Тело массой в 3 кг движется прямолинейно по законуS=1+t+t²,Sвыражено в сантиметрах,t– в секундах. Определить кинетическую энергию (mv²/2) тела через 5 секунд после начала движения.

5.153.Уголповорота шкива в зависимости от времениtзадан функцией=t²+3t–5.найти угловую скорость приt=5 секунд.

5.154. Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 8 секунд. Найти угловую скорость  через 32 секунды после начала движения.

5.155. Угол , на которой поворачивается колесо через t секунд равен =at²–bt+c, где a, b, c – положительные постоянные. Найти угловую скорость  движения колеса. В какой момент времени угловая скорость будет равна нулю?

5.156. Количество электричества, протекшее через проводник, начиная с момента времени t=0, дается формулой Q=2t²+3t+1 (кулонов). Найти силу тока в конце пятой секунды.

5.157. Канат висящего моста имеет вид параболы и прикреплен к вертикальным опорам, отстоящим одна от другой на 200 м. Самая нижняя точка каната находится на 40 м. ниже точек подвеса. Найти угол между канатом и опорными колоннами (см. рис. 1).

Указание. Сначала, исходя из условия задачи, составить уравнение параболы, т.е. найти величину k в уравнении y=kx².

рис.1.

5.158. Неоднородный стержень АВ имеет длину 12 см. Масса его части АМ растет пропорциональный квадрату расстояния текущей точки М от конца А и равна 10г. при АМ=2см. Найти массу всего стержня АВ и линейную плотность в любой его точке М. Чему равна линейная плотность стержня в точках А и В.

5.159. Тяжелую балку длиной 13 м. спускают на землю так, что ее нижний конец прикреплен к вагонетке (см. рис.), а верхний удерживается канатом, намотанным на ворот. Канат сматывается со скоростью 2м/мин. С каким ускорением отталкивается вагонетка в момент, когда она находится на расстоянии 5 м. от точки О.

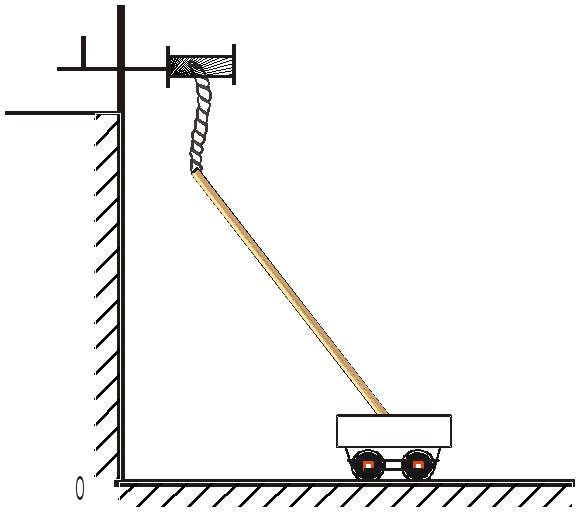
5.160. Баржу, палуба которой на 4 м. ниже пристани, подтягивают к ней при помощи каната, наматываемого на ворот со скоростью 2м/сек. С каким ускорением, движется баржа в момент, когда она удалена от пристани на 8 м. (по горизонтали).