
Задачник по линейной Алгебре и Мат Анализу / Часть 3
.doc3. Аналитическая геометрия
Прямая на плоскости
-
Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями
 Определить координаты его вершин.
Определить координаты его вершин.
-
Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oy, для каждой из прямых:
![]()
![]()
-
Даны вершины треугольника
 и
и
 Составить уравнения его высот.
Составить уравнения его высот. -
Даны уравнения двух сторон прямоугольника

 и одна из его вершин
и одна из его вершин
 Составить уравнения двух других сторон
этого прямоугольника.
Составить уравнения двух других сторон
этого прямоугольника. -
Составить уравнения прямых, проходящих через вершины треугольника

 параллельно противоположным сторонам.
параллельно противоположным сторонам. -
Даны вершины треугольника
 и
и
 Составить уравнение перпендикуляра,
опущенного из вершины А на медиану
проведенную из вершины В.
Составить уравнение перпендикуляра,
опущенного из вершины А на медиану
проведенную из вершины В. -
Написать уравнения сторон и найти углы треугольника с вершинами
 и
и

-
Составить уравнения сторон и медиан треугольника с вершинами

-
Определить угол
 между
двумя прямыми:
между
двумя прямыми:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
-
Даны две противоположные вершины квадрата
 и
и
 Составить уравнения его сторон.
Составить уравнения его сторон. -
Даны две вершины треугольника
 его высоты пересекаются в точке
его высоты пересекаются в точке
 Определить координаты третьей вершины
Определить координаты третьей вершины

-
Вычислить площадь треугольника, отсекаемого прямой
 от координатного угла.
от координатного угла. -
Составить уравнение прямой, которая проходит через точку
 и отсекает от координатного угла
треугольник с площадью, равной 12 кв.ед.
и отсекает от координатного угла
треугольник с площадью, равной 12 кв.ед. -
Точка
 является вершиной квадрата, одна из
сторон которого лежит на прямой
является вершиной квадрата, одна из
сторон которого лежит на прямой
 Вычислить площадь этого квадрата.
Вычислить площадь этого квадрата. -
Даны вершины треугольника:
 и
и
 .
Вычислить длину перпендикуляра,
опущенного из вершины B
на медиану, проведенную из вершины С.
.
Вычислить длину перпендикуляра,
опущенного из вершины B
на медиану, проведенную из вершины С. -
Вычислить расстояние d между параллельными прямыми:
1) 3x–4y–10=0, 6x–8y+5=0; 2) 5x–12y+25=0, 5x–12y–13=0;
3) 4x–3y+15=0, 8x–6y+25=0; 4) 24x–10y+39=0, 12x–5y–26=0.
3.17. Найти уравнения биссектрис угла,
образованного прямыми
![]() и
и
![]() .
Проверить, что биссектрисы перпендикулярны.
.
Проверить, что биссектрисы перпендикулярны.
3.18. Найти биссектрису внутреннего
угла
![]() треугольника
треугольника
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
3.19. Даны две вершины
![]() и
и
![]() треугольника
треугольника
![]() и точка
и точка
![]() пересечения его высот. Найти уравнения
всех сторон треугольника.
пересечения его высот. Найти уравнения
всех сторон треугольника.
3.20. В треугольнике
![]() даны уравнения стороны
даны уравнения стороны
![]() :
:
![]() и биссектрис
и биссектрис
![]() и
и
![]() .
Найти координаты вершин треугольника.
.
Найти координаты вершин треугольника.
3.21. Даны уравнения сторон
![]()
![]() ,
,
![]() и точка
и точка
![]() пересечения его медиан. Найти уравнение
пересечения его медиан. Найти уравнение
![]() .
.
3.22. Даны две высоты треугольника
![]()
![]() и
и
![]() и координаты одной из вершин
и координаты одной из вершин
![]() .
Найти уравнения всех сторон треугольника.
.
Найти уравнения всех сторон треугольника.
3.23. Даны две смежные вершины
параллелограмма
![]() и
и
![]() ,
точка
,
точка
![]() пересечения диагоналей. Найти уравнения
двух других сторон и диагоналей
параллелограмма.
пересечения диагоналей. Найти уравнения
двух других сторон и диагоналей
параллелограмма.
-
Даны уравнения двух сторон квадрата

 и
одна из его вершин
и
одна из его вершин
 Составить уравнения двух других сторон
этого квадрата.
Составить уравнения двух других сторон
этого квадрата. -
Из точки
 выходит
луч света под углом
выходит
луч света под углом
 к оси Ox и отражается
от оси Ox, а затем от
оси Oy. Написать
уравнения всех трех лучей.
к оси Ox и отражается
от оси Ox, а затем от
оси Oy. Написать
уравнения всех трех лучей. -
Даны уравнения боковых сторон равнобедренного треугольника
 и точка
и точка
 лежащая
на его основании. Составить уравнение
основания треугольника.
лежащая
на его основании. Составить уравнение
основания треугольника. -
Даны одна из вершин треугольника (1;3) и уравнения двух медиан x–2y+1=0 и y–1=0. Составить уравнения его сторон.
Плоскость в пространстве.
-
Составить уравнение плоскости, которая проходит через точку
 и имеет нормальный вектор
и имеет нормальный вектор

-
Точка
 служит основанием перпендикуляра,
опущенного из начала координат на
плоскость. Составить уравнение этой
плоскости.
служит основанием перпендикуляра,
опущенного из начала координат на
плоскость. Составить уравнение этой
плоскости. -
Даны две точки
 и
и
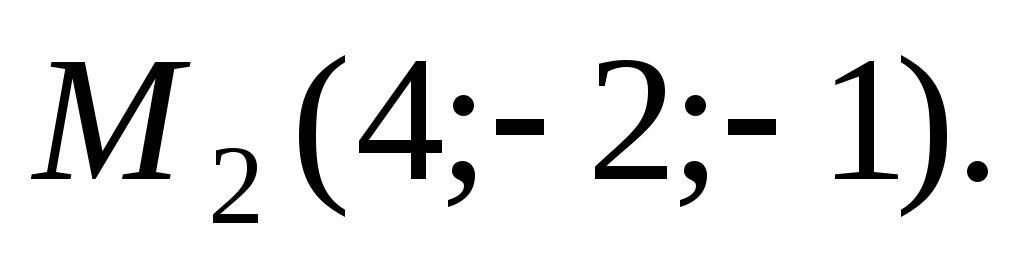 Составить уравнение плоскости,
проходящей через точку
Составить уравнение плоскости,
проходящей через точку
 перпендикулярно
вектору
перпендикулярно
вектору

-
Составить уравнение плоскости, проходящей через точку M1(3;4;–5) параллельно двум векторам
 ={3;1;–1}
и
={3;1;–1}
и
 ={1;–2;1}.
={1;–2;1}. -
Составить уравнение плоскости, проходящей через точки
 и
и
 параллельно вектору
параллельно вектору

-
Составить уравнение плоскости, проходящей через три точки
 и
и

-
Определить двугранные углы, образованные пересечением следующих пар плоскостей:
![]()
![]()
![]()
-
Составить уравнение плоскости, которая проходит через точку
 параллельно плоскости
параллельно плоскости

-
Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям:
 .
. -
Составить уравнение плоскости, которая проходит через точку
 перпендикулярно к двум плоскостям
перпендикулярно к двум плоскостям
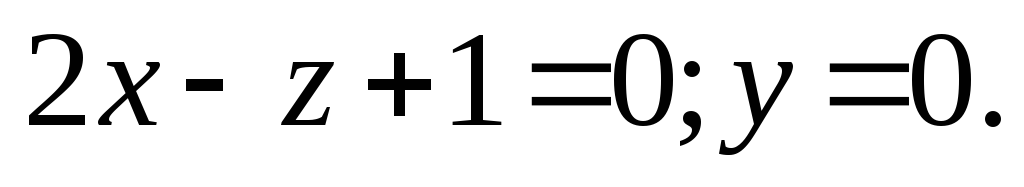
-
Состаивть уравнение плоскости, которая проходит через две точки
 и
и
 перпендикулярно
к плоскости
перпендикулярно
к плоскости

-
Составить уравнение плоскости, которая проходит:
1) через точки
![]() и
и
![]() параллельно оси Ox;
параллельно оси Ox;
2) через точки
![]() и
и
![]() параллельно оси Oy;
параллельно оси Oy;
3) через точки
![]() и
и
![]() параллельно оси Oz.
параллельно оси Oz.
-
Вычислить объем пирамиды, ограниченной плоскостью
 и координатными плоскостями.
и координатными плоскостями. -
Составить уравнение плоскости, параллельной вектору
 и отсекающей на координатных осях Ox
и Oy отрезки a=3,
b=-2.
и отсекающей на координатных осях Ox
и Oy отрезки a=3,
b=-2. -
Вычислить расстояние d от точки
 до плоскости, проходящей через три
точки
до плоскости, проходящей через три
точки
 и
и
 .
. -
Две грани куба лежат на плоскостях

 Вычислить объем этого куба.
Вычислить объем этого куба. -
Написать уравнение плоскости, проходящей через ось Ox и составляющей угол 600 с плоскостью y=x.
-
Написать уравнения плоскостей, параллельных плоскости
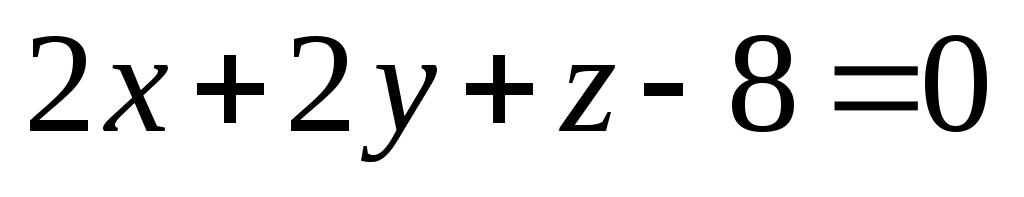 и
удаленных от нее на расстояние d=4.
и
удаленных от нее на расстояние d=4. -
Написать уравнение плоскости, проходящей через линию пересечения плоскостей
 и
и
 и перпендикулярной плоскости
и перпендикулярной плоскости

-
Установить, что плоскости
 ,
,
 и
и
 имеют единственную общую точку. Найти
её.
имеют единственную общую точку. Найти
её. -
Найти высоту пирамиды
 ,
опущенную из вершины
,
опущенную из вершины
 на грань
на грань
 ,
если
,
если
 ,
,
 ,
,
 ,
,
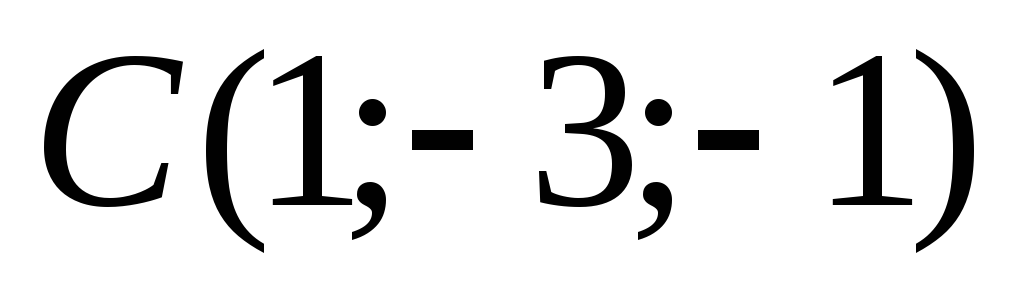 .
. -
Найти уравнение плоскости, проходящей через точки
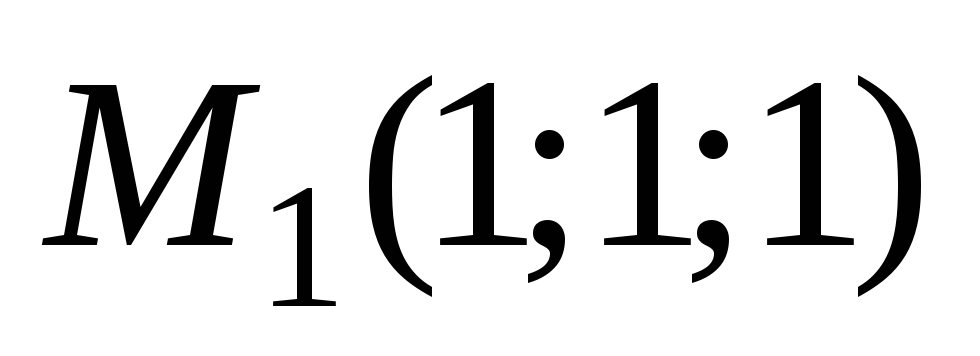 ,
,
 параллельно прямой, проходящей через
параллельно прямой, проходящей через
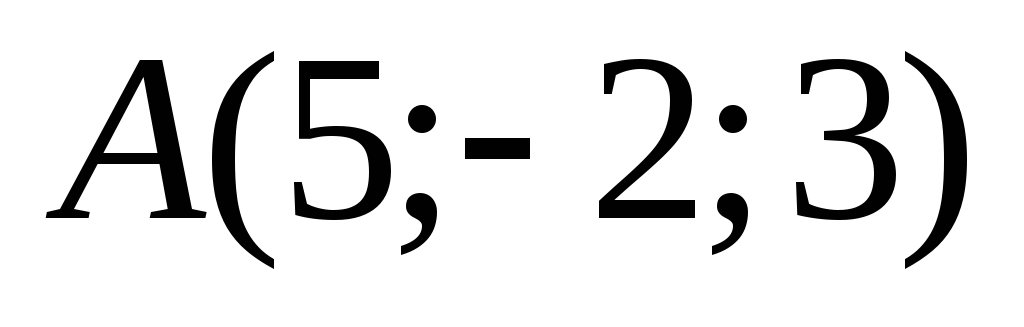 и
и
 .
.
