Ответы.

1. .2. .3. .4. .5. .

7. .8. .

9. .10. .

11. .12. .

13. .14. .

15. .16. .

17. . 18.. 19..

20. . 21.. 22..

23. . 24.. 25..

26. . 27. .

28. .29. .30. .31. .32. .33. .34. .35. .36. .37. .38. .39. .40. .

41. .42. .43.

44. .45. .46. .47. .48. .

49 .50. .

51. .52. .

53. .54. .

55. .56. .

57. .

58. .

59.

60. .

61. .

62. .

63. .

64. .

65. .66. .

67. .68. .

69. .70. .

71. .72. .73. .74. .

75. .76. .77. .

78. .79. .80. .81. .

82. .83. .84. .85. .86. .

87. .88. .89. .

90. .

91.

. 92. .93. .

94. .95. .96. .97. .

98. .99. .100. .101. .

102. .103. .104.

105. .106. .

107. .

108. .

109. .

110. , если, если.

111. , если, если

112. , если, если.

113. .114. . 115..

116. .

117. .

118. а) ; б). 119.. 120.. 121. .

122. а) ; б).

123. а) ; б).124. а) ; б).

125. а) 3,8; б) 0,005; -0,01. 126. .127. 1,22. 128. 0,57. 129. 0,44. 130. 0,02. 131. 1,01. 132. 0,8. 133. 2,03. 134. –0,72. 135. 1,04.

Задания для индивидуальной работы.

Вариант 1

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g)

2. Найти точку на кривой касательная в которой параллельна прямой

Вариант 2

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;g)

2. Закон движения материальной точки . Найти ее скорость в момент времени

Вариант 3

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;

f) ;g)

2. Выяснить, в какой точке кривой касательная параллельна прямой

Вариант 4

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;

g)

2. Выяснить, в каких точках кривой касательная составляет с осьюугол

Вариант 5

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g)

2. Составить уравнение касательной к кривой в точке.

Вариант 6

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;g)

2. Найти тангенсы углов , под которыми прямаяпересекается с кривой

Вариант 7

1. Найти следующих функций:

a) ;

b) ;c) ;

d) ;e) ;

f) ;g)

2. Кривая задана уравнением: Определить угол между касательными к кривой в точках с абсциссамии

Вариант 8

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2. По оси движутся две материальные точки, законы движения которыхи. В какой момент времени их скорости будут равными?

Вариант 9

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2. Найти угол между кривыми: и

Вариант 10

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g) .

2. Составить уравнение касательной в точке к кривой, заданной параметрически:.

Вариант 11

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g) .

2. Найти точку на кривой касательная в которой перпендикулярна прямой

Вариант 12

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;g) .

2. Закон движения материальной точки . Найти ее скорость в момент времени

Вариант № 13

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;

f) ;g) .

2. Закон движения материальной точки . Найти скорость ее движения в момент времени.

Вариант 14

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;

g)

2. Записать уравнение нормали к кривой в точке с абсциссой

Вариант 15

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g)

2. Составить уравнение касательной к кривой в точке.

Вариант 16

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;g)

2. В какой точке параболы ордината возрастает в три раза быстрее, чем абсцисса?

Вариант 17

1. Найти следующих функций:

a) ;

b) ;c) ;

d) ;e) ;

f) ;g)

2. Найти точку на кривой , касательная в которой параллельна прямой.

Вариант 18

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2. В какой точке кривой касательная составляет с осью угол?

3. Вычислить приближенно с помощью дифференциала .

Вариант 19

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2.Найти точки на кривой в которых касательные параллельны оси

Вариант 20

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g) .

2. Составить уравнение касательной в точке к кривой , заданной в точке с абсциссой

Вариант 21

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g) .

2. Составить уравнение касательной в точке к кривой, заданной параметрически:.

Вариант 22

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g) .

2. Найти угол, под которым пересекаются кривые и

Вариант 23

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;g) .

2. Найти угол наклона (к оси ) касательных к параболев точках:.

Вариант 24

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;

f) ;g) .

2. Составить уравнения касательных, проведенных к параболе в точке (1;-3).

Вариант 25

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;

e) ;f) ;

g)

2. Найти значения , при которых касательные к графику функциипараллельны прямой(Рекомендуется сделать пояснительный рисунок)

3. Вычислить приближенно с помощью дифференциала .

Вариант 26

1. Найти следующих функций:

a) ;

b) ;

c) ;

d) ;e) ;

f) ;g)

2. Составить уравнение нормали к кривой в точке.

Вариант 27

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;g)

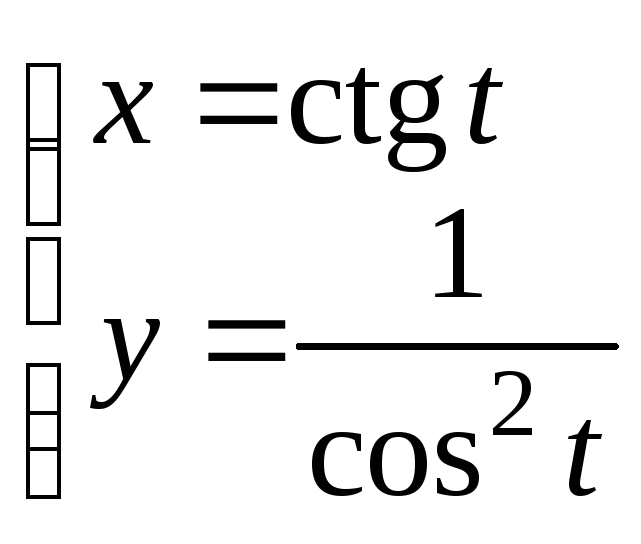
2. Написать уравнения касательных к кривой в точках ее пересечения с осью

Вариант 28

1. Найти следующих функций:

a) ;

b) ;c) ;

d) ;e) ;

f) ;g)

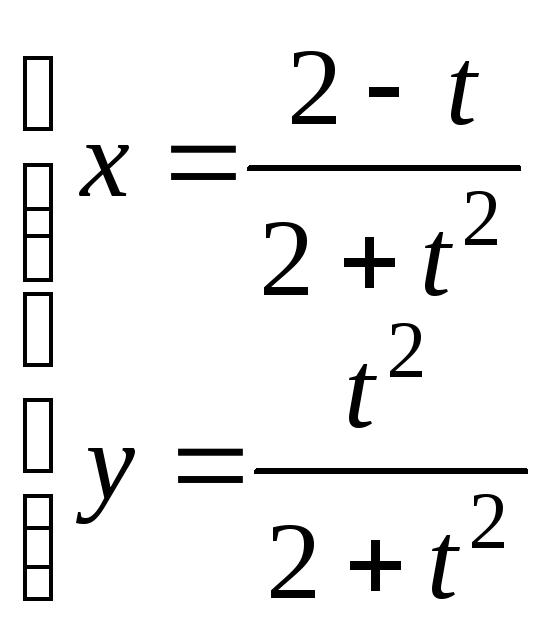
2. Составить уравнения касательных к кривой в точке (2;3).

Вариант 29

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2. В какой точке кривой касательная составляет с осью угол?

Вариант № 30

1. Найти следующих функций:

a) ;

b) ;

c) ;d) ;

e) ;f) ;

g)

2.Составить уравнения касательной к кривой в точке (1;-1).

162