§ 5 Производная и дифференциал функции.

Функция называется дифференцируемой в точке, если существует предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю,

.

Предел называется производной и обозначаетсяили.

Основные правила дифференцирования.

Пусть ,– дифференцируемые в точкефункции.

1. ;

2. ;

3. ;

4. .

5. Если , где, т.е.– сложная функция, то ее производная.

6. Если функция задана параметрически 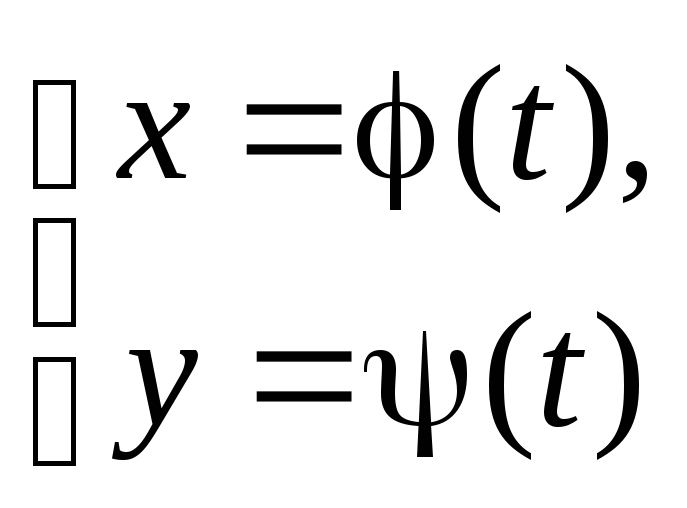, то ее производная.

Дифференциалом функции называется главная часть ее приращения, линейная относительно приращения аргумента и обозначается.

Если ,при, то.

Дифференциал независимого аргумента равен приращению аргумента, т.е. .

Таким образом, .

Формула приближенного вычисления .

Производная функции в точкеравна угловому коэффициенту касательной, проведенной к графику функции в этой точке (геометрический смысл производной).

Производная функции в точкеравна скорости изменения функции в этой точке (физический смысл производной).

Таблица производных основных элементарных функций

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. .

Найти производные функций, используя определение.

Пример 5.1. .

Решение.

Дадим аргументу приращение, тогда значение функции.

Найдем приращение функции

Теперь найдем предел отношения при:

.

Итак, .

Пример 5.2. .

Решение.

Дадим аргументу приращение, значение функции. Найдем приращение функции

Используем формулу

.

Перейдем к пределу отношения при:

.

Таким образом, .

Найти производные функций используя правила и таблицу производных.

Пример 5.3. .

Решение.

Перейдем к дробным показателям: .

.

Пример 4. .

Решение:

Пример 5.5. .

Решение.

.

Пример 5.6. .

Решение.

Пример 5.7. .

Решение.

Используя свойства логарифмов, преобразуем правую часть:

.

Найдем производную

Пример 5.8. .

Решение.

Пример 5.9. .

Решение.

Сначала логарифмируем данную функцию по основанию, т.е.

,

,

.

Теперь дифференцируем обе части равенства по правилу дифференцирования сложной функции.

,

,

,

.

Пример 5.10. .

Решение.

Логарифмируем данную функцию

,

.

Дифференцируем обе части равенства

,

,

,

,

.

Пример 5.11. .

Решение.

Производная параметрической функции находится по формуле .

.

.

.

Пример 5.12. .

Решение.

Данная функция неявно заданная. Найдем ее производную, рассматривая при этом как функцию от.

,

,

,

,

,

.

Пример 5.13. Используя понятие дифференциала, приближенно вычислить .

Решение. Используем формулу приближенного вычисления: ., тогда. Положим(соответствует углу в 1⁰), . Подставляем в формулу имеем:

Решение задач на геометрический смысл производной основано на использовании уравнения касательной:

Угловой коэффициент касательной равен, с одной стороны тангенсу угламежду касательной и осью абсцисс, а с другой – значению производной функциив точке,

Пример 5.14. Составить уравнения касательной и нормали к кривой в точке.

Решение. Для составления уравнения касательной используем формулу , где,.

Таким образом, или– уравнение касательной.

Для составления уравнения нормали используем формулу . Получим,,- уравнение нормали.

Пример 5.15. В какой точке касательная к графику функции а) параллельна прямой? б) перпендикулярна прямой?

Решение. а) Прямая параллельна касательной, если их угловые коэффициенты равны. Угловой коэффициент прямой равен, угловой коэффициент касательной равен, где– точка касания.

Из уравнения находим.

Значит касательная должна быть проведена в точке .

б) Прямая перпендикулярна касательной если их угловые коэффициенты . Так как, то. Из уравнениянаходим.

Таким образом, касательная должна быть проведена в точке .

Пример 5.16. В какой точке параболы ордината возрастает вдвое быстрее, чем абсцисса?

Решение. Найдем производную функции .

Так как производная функции характеризует скорость возрастания ординаты (функции) по сравнению с возрастанием аргумента, то по условию задачи , откуда– абсцисса искомой точки.

Ордината .

Таким образом – искомая точка.

Производной второго порядка от функции называется производная от ее производной, т.е.и обозначается

.

Если – закон прямолинейного движения точки, то– ускорение этого движения.

Производная -го порядка от функции называется производная производной-го порядка:и обозначается.

Производные высших порядков вычисляются последовательным дифференцированием данной функции.

Пример 5.17. . Найти.

Решение. Найдем производную данной функции: .

Вторая производная – производная от первой производной:

.

Пример 5.18. . Найти.

Решение. ,,,.

Очевидно, что каждая из найденных производных равна произведению нав степени, равной порядку производной. Эта закономерность сохраняется для производной любого порядка. Поэтому.