Задания для индивидуальной работы .
Даны координаты вершин треугольника
.Составить
уравнения стороны
,
высоты
и
медианы
;
найти длину
,
высоты
,
угол
.
В треугольной пирамиде
даны координаты вершин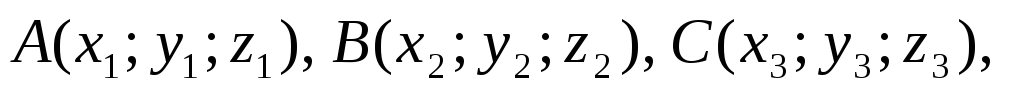
.
Найти: объем пирамиды; площадь грани
;
уравнение плоскости
;
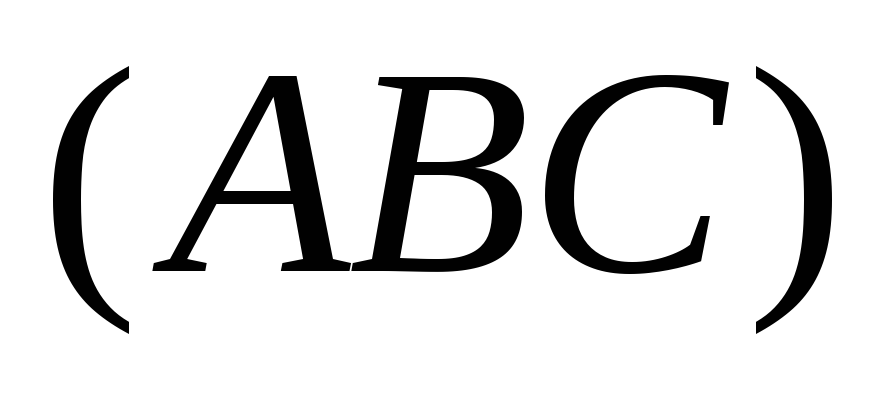уравнение ребра
(канонические
и общие); угол между ребром
и
плоскостью
;
уравнения и длину высоты
,
проведенной из вершины на грань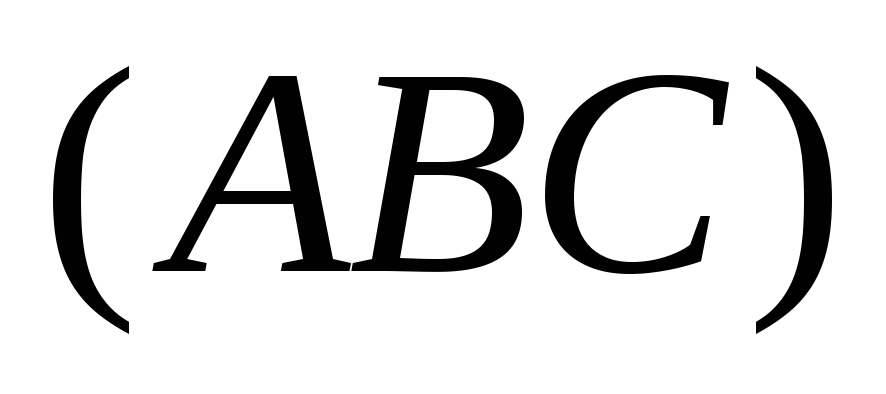
;
координаты пересечения высоты
с
гранью
.
Вариант №1
.
.
Вариант №2
.
.
Вариант №3
1.
.
2.
.
Вариант №4
1.
.
2.
.
Вариант №5
1.
.
2.
Вариант №6
1.
.
2.
Вариант №7
1.
.
2.
Вариант №8
1.
.
2.
Вариант №9
1.
.
2.
Вариант №10
1.
.
2.
Вариант №11
1.
.
2.
.
Вариант №12
1.
.
2.
.
Вариант №13
1.
.
2.
.
Вариант №14
1.
.
2.
.
Вариант №15
1.
.
2.
Вариант №16
1.
.
2.
Вариант №17
1.
.
2.
Вариант №18
1.
.
2.
Вариант №19
1.
.
2.
Вариант №20
1.
.
2.
Вариант №21
1.
.
2.
.
Вариант №22
1.
.
2.
.
Вариант №23
1.
.
2.
.
Вариант №24
1.
.
2.
.
Вариант №25
1.
.
2.
Вариант №26
1.
.
2.
Вариант №27
1.
.
2.
Вариант №28
1.
.
2.
Вариант №29
1.
.
2.
Вариант №30
1.
.
2.
.
Вариант №31
1.
Даны координаты вершин треугольника
.
Найти уравнение прямой через точку
и перпендикулярно медиане, проведенной
из вершины
.
2.
Найти уравнение прямой
,
если
3.
Найти уравнение плоскости
где
4.
Найти уравнение линии, точки которой
равноудалены от
и от прямой
Вариант №32
1.
Даны координаты вершин треугольника
.
Найти уравнение медианы и высоты,
проведенной из вершины
.
2.
Даны
.
Найти уравнение прямой, проходящей
через
перпендикулярно плоскости
.
3.
Найти уравнение плоскости
.
4. Найти уравнение
кривой, отношение расстояний точек
которой до точки
и до прямой
равно
Вариант №33
1.
Даны координаты вершин треугольника
.
Найти расстояние от вершины
,
до медианы, проведенной из вершины
.
2.
Привести уравнение прямой
к
каноническому виду
3.
Найти уравнение плоскости
.
4.
Найти уравнение линии, расстояние точек
которой от
и
от
относятся друг к другу как 2:3.
Вариант №34
1.
Даны координаты вершин треугольника
.
Найти уравнение и длину высоты
.
2.
Дано
Найти уравнение прямой,
если
3.
Найти расстояние от точки
до прямой.
4.
Найти уравнение линии, каждая точка
которой вдвое дальше от
,чем
от
.
Вариант №35
1.
Даны координаты вершин треугольника
.
Найти уравнение прямой через точку
и перпендикулярно медиане, проведенной
из вершины
.
2.
Найти уравнение прямой
,
проходящей через
параллельно плоскости
и перпендикулярно прямой
3.
Найти уравнение плоскости
проходящей через две точки
и
,
и параллельно прямой
4.
Найти уравнение линии, точки которой
равноудалены от
и от прямой
Вариант №36
1.
Даны координаты вершин треугольника
.
Найти расстояние от вершины
,
до медианы, проведенной из вершины
.
2.
Привести уравнение прямой
к
каноническому виду
3.
Найти уравнение плоскости
проходящей через точку
и прямую
.
4.
Найти уравнение линии, расстояние точек
которой от точек
и
относятся друг к другу как 1:2.
Вариант №37
1. Даны координаты
двух вершин треугольника
и
– точка пересечения высот треугольника.
Найти координаты вершины
.
2.
Из
восставлен перпендикуляр на
в
точку
.
Найти уравнение плоскости
.
3.
Найти точку пересечения прямой
и плоскости
4.
Составить уравнение геометрического
места точек, для каждой из которых сумма
квадратов расстояний до точек
и
равна 70.
Вариант №38
1.
Стороны треугольника заданы уравнениям:
Найти координаты вершин треугольника
и уравнение одной из высот.
2.
Через линию пересечения плоскостей
и
провести плоскость, проходящую через
начало координат
3.
Найти канонические уравнения прямой,
проходящей через точку
,
перпендикулярно
,
содержащей точки
,
и
.
4.
Составить уравнение геометрического
места точек, равноудаленных от линий:
и
Вариант №39
1. Стороны ромба
заданы уравнениями
уравнение
одной из диагоналей
Найти
координаты вершин ромба и вычислить
его площадь.
2.
Составить уравнение плоскости, проходящей
через точки
и
,
и перпендикулярно плоскости
3.
Написать параметрические уравнения
прямой
.
4.
Составить уравнение геометрического
места точек, отстоящих от точки
на
расстоянии 4.