§ 2. Элементы векторной алгебры.

Суммой векторов иназывается вектор, соединяющий начало векторас концом вектораи обозначаетсяили(правило треугольника).

Суммой векторов и, начала которых совпадают, называются вектор с тем же началом, совпадающий с диагональю параллелограмма, сторонами которого являются векторыи.(правило паралеллограма).

Разность этих векторов изображается вектором, совпадающим со второй диагональю того же параллелограмма, т.е..

Произведением вектора на числоназывается вектор, коллинеарный вектору; сонаправленный с векторомеслии противоположно направленный вектору, если.

.

Если известны координаты точек и, то координаты вектора.

Координаты вектора являются его проекциями на координатные оси, поэтомуможет быть представлен в виде:, где– единичные ортогональные векторы.

Модуль вектора определяется по формуле

.

Если вектор образует с осямиуглы, то

направляющие косинусы вектора .

Если и, то

, .

Следовательно, условием коллинеарности векторов иявляется пропорциональность их координат.

Пример 2.1.

Вектор , длина которого равна 6, образует с осьюугол 60⁰, с осью – угол 135⁰, с осью – угол 90⁰. Найти проекции вектора на данные оси.

Решение.

,

,

.

Скалярным произведением двух векторов называется произведение их модулей, умноженное на косинус угла между ними

Свойства скалярного произведения.

1. ;

2. ;

3. ;

4. если ненулевые векторы , тои обратно;

5. если , то

.

Косинус угла между векторами иопределяется по формуле

.

Пример 2.2.

Найти угол между двумя векторами и.

Решение.

По формуле найдем

, отсюда .

Векторным произведением вектора на векторназывается вектор, определяемый следующим образом:

1) модуль вектораравен произведению модулей векторовина синус угла между ними:;

2) и;

3) вектор направлен так, что смотря из его конца кратчайший поворот от вектораквиден против часовой стрелки.

Свойства векторного произведения.

1) ;

2) ;

3) ;

4) если , то;

5) если и, то;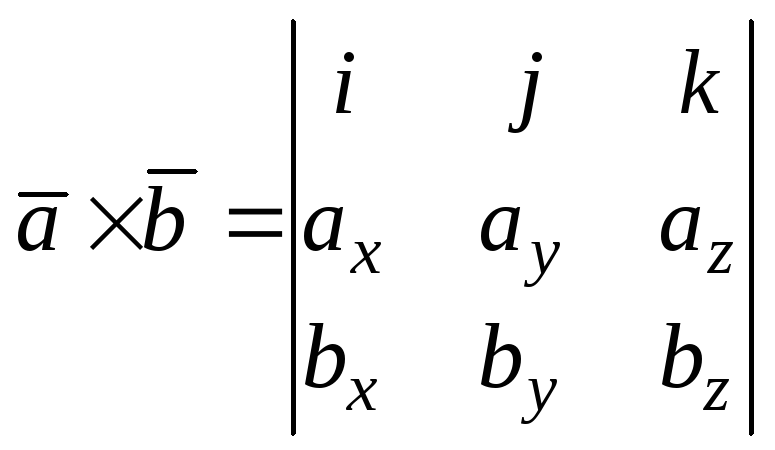

6) модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.

Пример 2.3.

Вычислить площадь треугольника с вершинами в точках

.

Решение.

Рассмотрим векторы и. Площадь треугольникаравна половине площади параллелограмма построенного на векторахи, т.е.

Найдем .

Таким образом, .

Следовательно, (кв.ед).

Смешанным произведением векторов иназывается скалярное произведение векторана вектори обозначаетсяили.

Свойства смешанного произведения.

1) ;

2) ;

3) если ,,, то

;

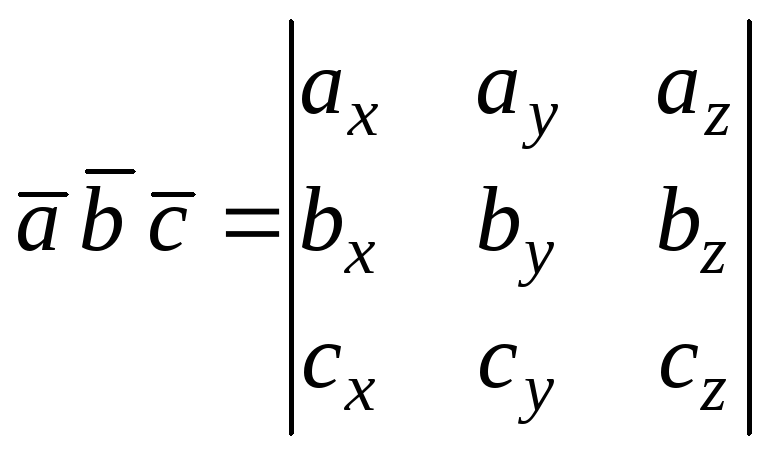4) смешанное произведение векторов численно равно объему параллелепипеда, построенного на этих векторах, т.е.

5) если ненулевые векторы компланарны, тои обратно.

Пример 2.4.

Показать, что векторы ,и

компланарны.

Решение: Найдем смешанное произведение векторов .

Так как смешанное произведение ненулевых векторов равно нулю, то векторы компланарны.

Пример 2.5. Найти объем пирамиды, построенной на векторах

Решение.

Объем пирамиды, построенной на векторах , равен одной шестой объема параллелепипеда, построенного на тех же векторах, т.е..

Найдем

.

Таким образом ,.