
- •Астраханский Государственный Технический Университет
- •§ 1. Элементы линейной алгебры.
- •Задания для самостоятельной работы
- •Задания для индивидуальной работы
- •§ 3. Элементы аналитической геометрии.
- •3. Уравнение прямой на плоскости
- •4. Уравнения плоскости.
- •5. Уравнение прямой в пространстве.
- •6. Кривые второго порядка.
- •Задания для самостоятельной работы
- •Задания для индивидуальной работы .
- •Задания для самостоятельной работы.
- •Задания для индивидуальной работы
- •Задание для самостоятельной работы
- •Ответы.
- •17. . 18.. 19..
- •20. . 21.. 22..
- •23. . 24.. 25..
- •116. .
- •2. Исследование функции на четность и нечетность.
- •3. Исследование функции на монотонность.
- •4. Исследование функции на экстремум.
- •5. Достаточные условия существования экстремума.
- •6. Выпуклость и вогнутость графика функции. Точки перегиба.
- •7. Асимптоты.
- •8. Схема исследования функции.
- •9. Наибольшее и наименьшее значения функции
- •Задачи для самостоятельной работы Исследование функции
- •Ответы.
- •Задания для индивидуальной работы
Задание для самостоятельной работы
Исходя из определения, найти производную функции





Доказать, что

Найти производную функции:
|
7. |
8. | |
|
9.
|
10.
| |
|
11.
|
12.
| |
|
13. |
14. | |
|
15.
|
16.
| |
|
17.
|
18.
| |
|
19.
|
20.
| |
|
21.
|
22.
| |
|
23.
|
24.
| |
|
25.
|
26.
| |
|
27.
|
28.
| |
|
29.
|
30.
| |
|
31.
|
32.
| |
|
33.
|
34.
| |
|
35.
|
36.
| |
|
37.
|
38.
| |
|
39.
|
40.
| |
|
41.
|
42.
| |
|
43.
|
44.
| |
|
45.
|
46.
| |
|
47.
|
48.
| |
|
49.
|
50.
| |
|
51.
|
52.
| |
|
53.
|
54.
| |
|
55.
|
56.
| |
|
57.
|
58.
| |
|
59.
|
60.
| |
|
61.
|
62.
| |
|
63.
|
64.
| |
|
65.
|
66.
| |
|
67.
|
68.
| |
|
69.
|
70.
| |
|
71.
|
72.
| |
|
73.
|
74.
| |
|
75.
|
76.
| |
|
77.
|
78.
| |
|
79.
|
80.
| |
|
81.
|
82.
| |
|
83.
|
84.
| |
|
85.
|
86.
| |
|
87.
|
89.
| |
|
90.
|
| |
Найти значения производных в данных точках:
 при
при
 и
и
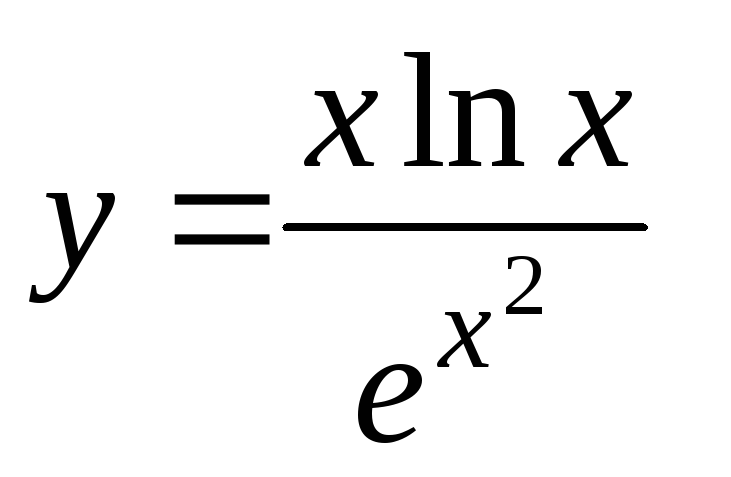 ;
;

Доказать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению .
.Доказать, что функция
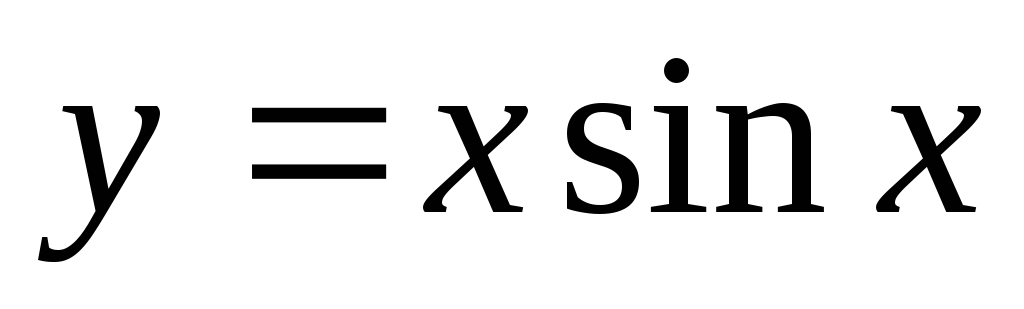 удовлетворяет уравнению
удовлетворяет уравнению .
.Доказать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению .
. .
Найти
.
Найти

 .
Найти
.
Найти

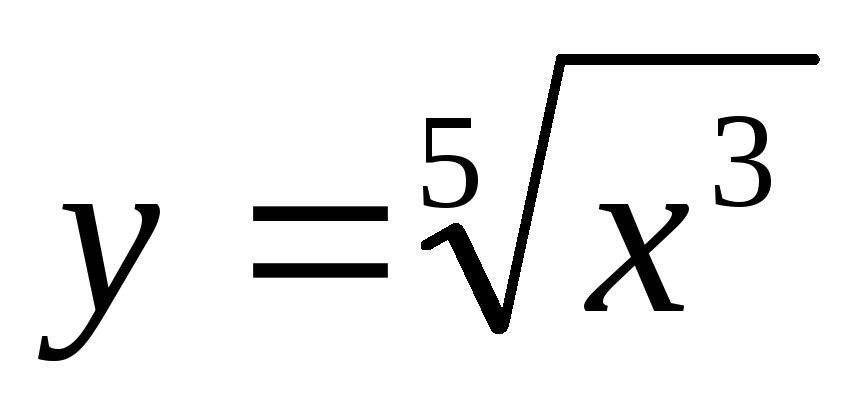 .
Найти
.
Найти

 .
Найти
.
Найти

 .
Найти
.
Найти

 .
Найти
.
Найти

 .
Найти
.
Найти

Найти
![]() от функций, заданных параметрически:
от функций, заданных параметрически:
|
103.
|
104.
|
|
105.
|
106.
|
|
107.
|
|
Найти производную n-го порядка
 .
.




Найти значения
производных порядка
![]() при
при![]() от нижеследующих функций:
от нижеследующих функций:
 .
. .
. .
.
Составить уравнение такой касательной к кривой
 ,
которая параллельна прямой
,
которая параллельна прямой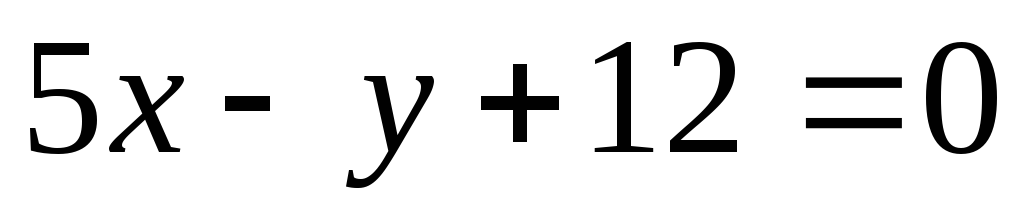
Составить уравнения касательной и нормали к кривой
 в точке с абсциссой
в точке с абсциссой .
.Найти тангенсы углов
 ,
под которым ось
,
под которым ось пересекается с кривой
пересекается с кривой .
.Составить уравнения касательной и нормали к кривой
 в точке
в точке .
.Составить уравнения касательной и нормали к кривой
 в точке
в точке .
.Какой угол образует с осью абсцисс касательная к графику функции, проведенная в указанной точке? Написать уравнение касательной: а)
 б)
б)

Составить уравнения касательной и нормали к кривой
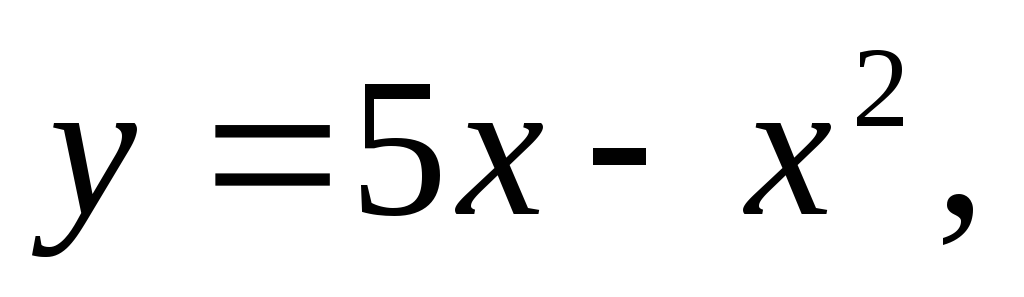 параллельной прямой, проходящей через
точки
параллельной прямой, проходящей через
точки и
и .
.Составить уравнения касательных к кривой
 перпендикулярных прямой
перпендикулярных прямой
Составить уравнение касательной к кривой
 перпендикулярной прямой, образующей
с осью абсцисс угол
перпендикулярной прямой, образующей
с осью абсцисс угол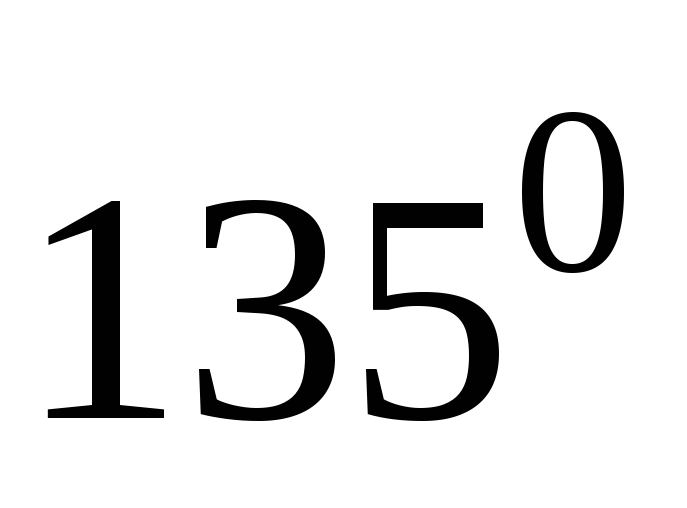 .
.Составить уравнения касательных к кривой
 а)
параллельных прямой
а)
параллельных прямой
 б)
перпендикулярных прямой
б)
перпендикулярных прямой

Составить уравнение касательной к кривой
 а)
проходящей параллельно биссектрисе
второго и четвертого координатных
углов; б)
отсекающей на оси абсцисс отрезок,
равный
а)
проходящей параллельно биссектрисе
второго и четвертого координатных
углов; б)
отсекающей на оси абсцисс отрезок,
равный

Найти угол между кривыми: а)
 и
и б)
б)
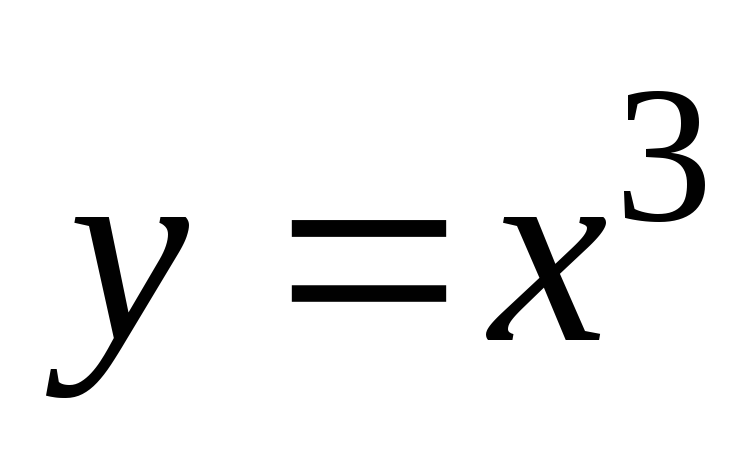 и
и
Тело движется прямолинейно по закону
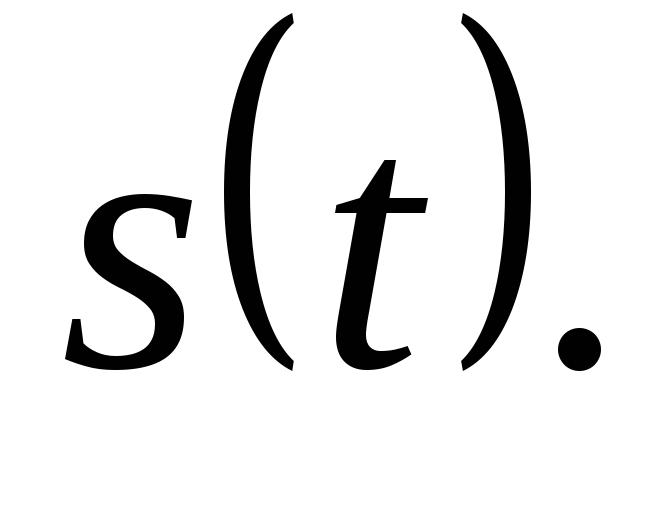 Определить скорость и ускорение тела
в указанный момент времени
Определить скорость и ускорение тела
в указанный момент времени а)
а)

Тело брошено вертикально вверх, движется по закону:
 Найти
начальную скорость и ускорение тела
Найти
начальную скорость и ускорение тела и максимальную высоту подъема (при
которой скорость
и максимальную высоту подъема (при
которой скорость ).
).
Используя понятие дифференциала, приближенно вычислить:
|
131.
|
132.
|
|
133.
|
134.
|
|
135.
|
136.
|
|
137.
|
138.
|
|
139.
|
|






