
- •Астраханский Государственный Технический Университет
- •§ 1. Элементы линейной алгебры.
- •Задания для самостоятельной работы
- •Задания для индивидуальной работы
- •§ 3. Элементы аналитической геометрии.
- •3. Уравнение прямой на плоскости
- •4. Уравнения плоскости.
- •5. Уравнение прямой в пространстве.
- •6. Кривые второго порядка.
- •Задания для самостоятельной работы
- •Задания для индивидуальной работы .
- •Задания для самостоятельной работы.
- •Задания для индивидуальной работы
- •Задание для самостоятельной работы
- •Ответы.
- •17. . 18.. 19..
- •20. . 21.. 22..
- •23. . 24.. 25..
- •116. .
- •2. Исследование функции на четность и нечетность.
- •3. Исследование функции на монотонность.
- •4. Исследование функции на экстремум.
- •5. Достаточные условия существования экстремума.
- •6. Выпуклость и вогнутость графика функции. Точки перегиба.
- •7. Асимптоты.
- •8. Схема исследования функции.
- •9. Наибольшее и наименьшее значения функции
- •Задачи для самостоятельной работы Исследование функции
- •Ответы.
- •Задания для индивидуальной работы
Задания для самостоятельной работы
По данным векторам
 и
и построить каждый из векторов: 1)
построить каждый из векторов: 1) ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.По данным векторам
 и
и построить каждый из векторов: 1)
построить каждый из векторов: 1) ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.Вычислить модуль вектора
 .
.Вычислить модуль вектора
 .
.На плоскости даны три единичных вектора
 так, что
так, что
 Построить вектор
Построить вектор и найти его длину.
и найти его длину.Даны точки

 .
Найти координаты вектора
.
Найти координаты вектора и
его длину.
и
его длину.Определить координаты начала вектора
 ,
если координаты его конца
,
если координаты его конца .
.Определить координаты конца вектора
 ,
если координаты начала совпадают с
точкой
,
если координаты начала совпадают с
точкой .
Найти модуль вектора
.
Найти модуль вектора .
.Вычислить длину и направляющие косинусы вектора
 .
.Вычислить направляющие косинусы вектора
 .
.Может ли вектор составлять с осями координат углы: 1)
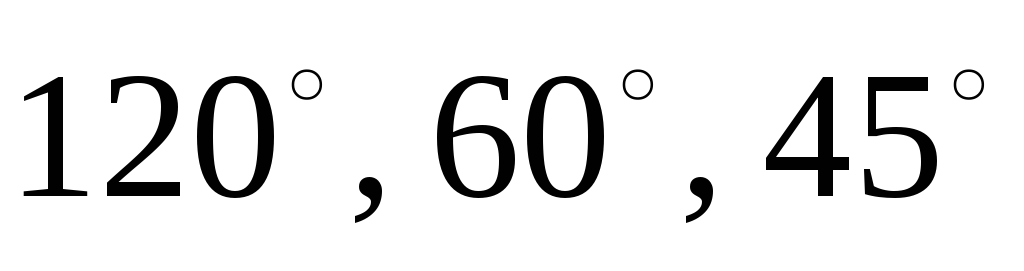 ;
2)
;
2) ?
?Если вектор составляет с осями
 и
и углы
углы и
и ,
то какой угол он составляет с осью
,
то какой угол он составляет с осью ?
?Даны векторы
 и
и .
Найти угол, образуемый вектором
.
Найти угол, образуемый вектором с осью
с осью .
.При каком значении
 векторы
векторы
 перпендикулярны?
перпендикулярны?Даны векторы
 и
и .
Найти проекцию вектора
.
Найти проекцию вектора на
вектор
на
вектор .
.На плоскости даны два вектора
 Найти разложение вектора
Найти разложение вектора по базису
по базису .
.Написать разложение вектора
 по векторам
по векторам ,
если эти векторы образуют базис:
,
если эти векторы образуют базис:
1)
![]()
![]()
2)
![]()
Векторы
 и
и образуют угол
образуют угол зная, что
зная, что ,
, ,
вычислить: 1)
,
вычислить: 1) ;
2)
;
2) ;
3)
;
3) ;
4)
;
4)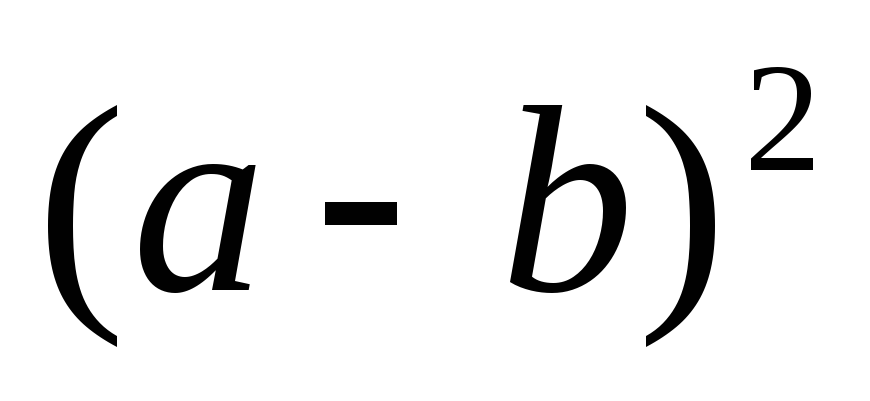 ;
;
5)
![]() .
.
Вычислить косинус угла, образованного векторами
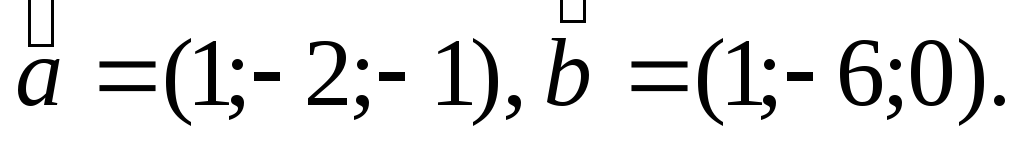
Дано, что
 ,
,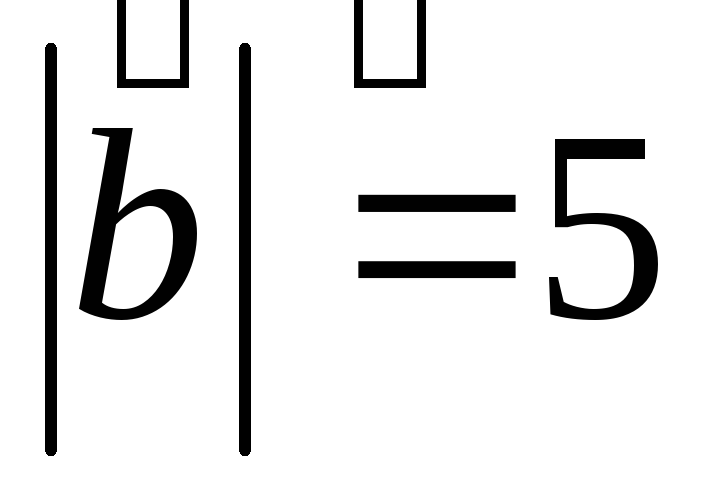 .
Определить, при каком значении
.
Определить, при каком значении векторы
векторы будут взаимно перпендикулярны.
будут взаимно перпендикулярны.Даны векторы
 ,
для которых
,
для которых ,
, ,
, .
Вычислить угол
.
Вычислить угол между медианой
между медианой и
стороной
и
стороной треугольника
треугольника
Найти координаты вектора
 ,
коллинеарного вектору
,
коллинеарного вектору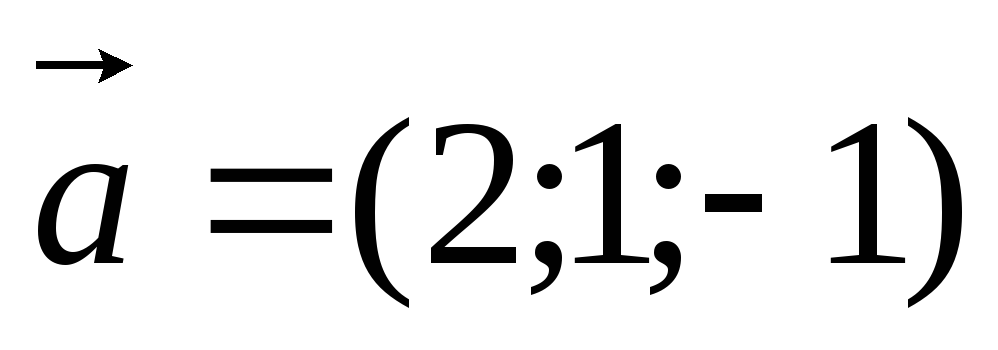 ,
при условии
,
при условии .
.Даны
 ,
, .
Найти координаты векторных произведений:
1)
.
Найти координаты векторных произведений:
1) ;
2)
;
2) 3)
3)
Векторы образуют угол
 .
Зная, что
.
Зная, что ,
, ,
вычислить
,
вычислить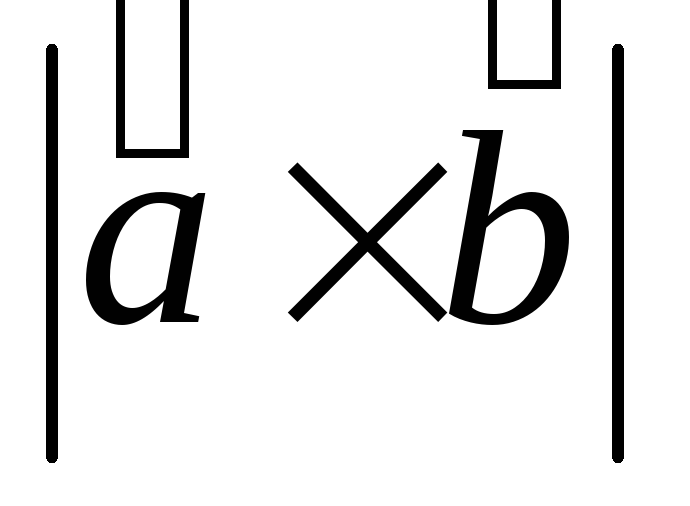 .
.Даны:
 ,
, и что
и что .
Вычислить
.
Вычислить .
.Даны точки

 и
и .
Найти координаты векторных произведений
1)
.
Найти координаты векторных произведений
1)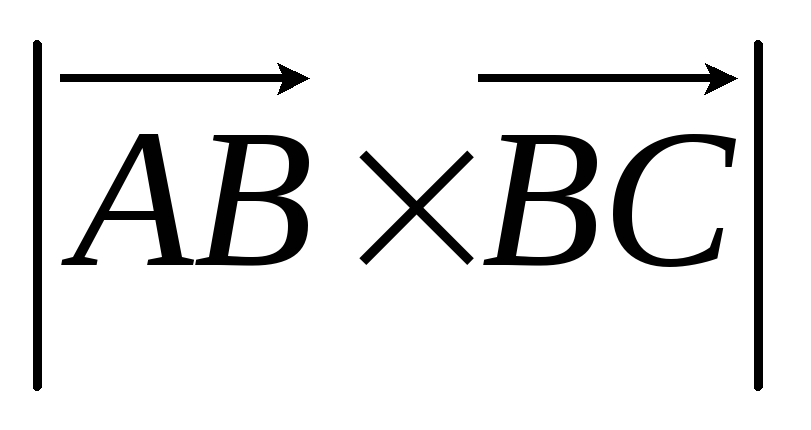 2)
2)
 .
.Даны координаты вершин треугольника

 и
и .
Вычислить его площадь.
.
Вычислить его площадь.Вычислить площадь параллелограмма, построенного на векторах
 ,
,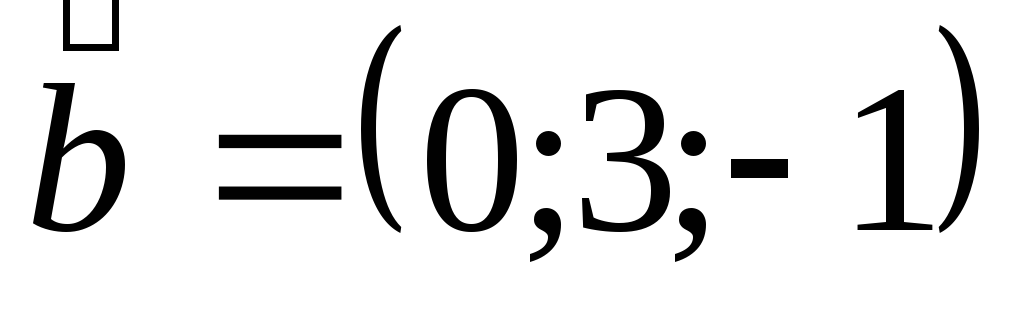 .
.Вычислить синус угла, образованного векторами
 и
и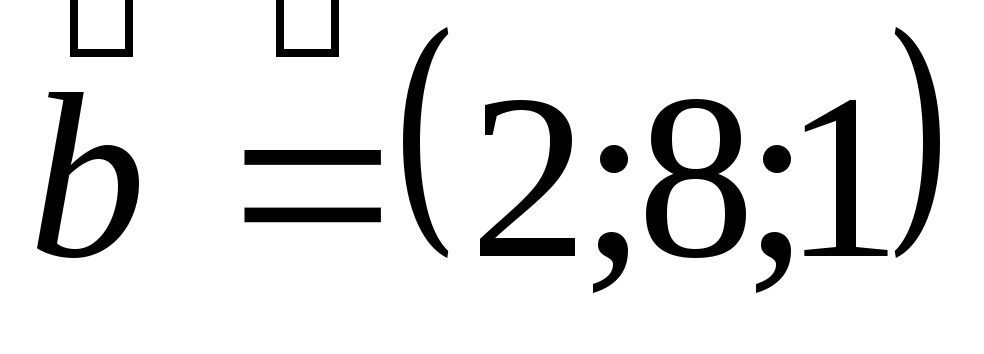 .
.Даны три вектора определить компланарны ли они: 1)
 ,
, ,
, ;
2)
;
2) ,
, ,
, .
.Компланарны ли векторы
 и
и ?
1)
?
1) ,
,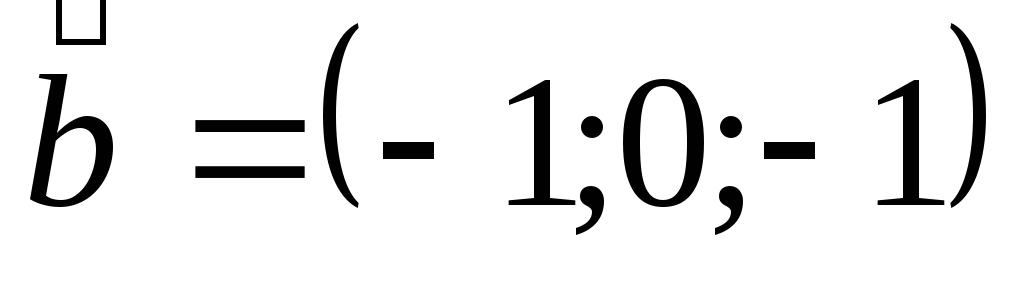 ,
, ;
2)
;
2) ,
, ,
,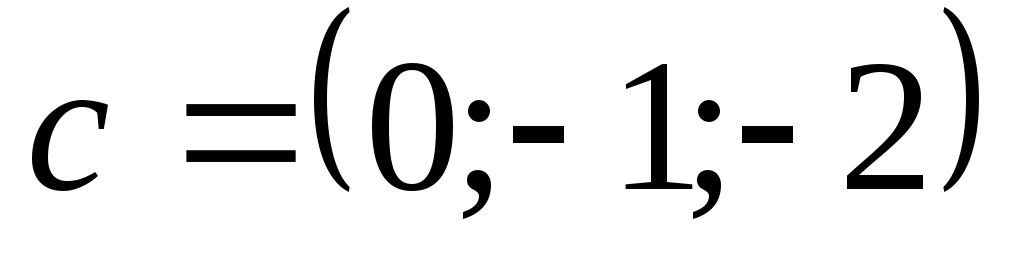 .
.Вектор
 перпендикулярен к векторам
перпендикулярен к векторам и
и ,
угол между
,
угол между и
и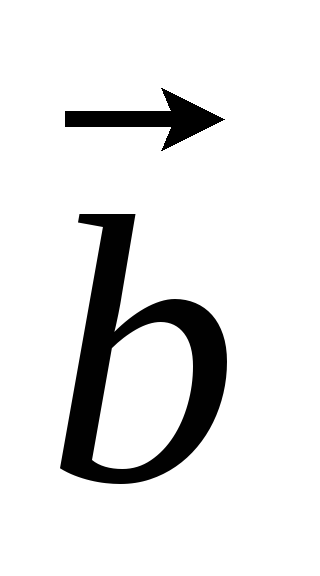 равен
равен .
Зная, что
.
Зная, что ,
вычислить
,
вычислить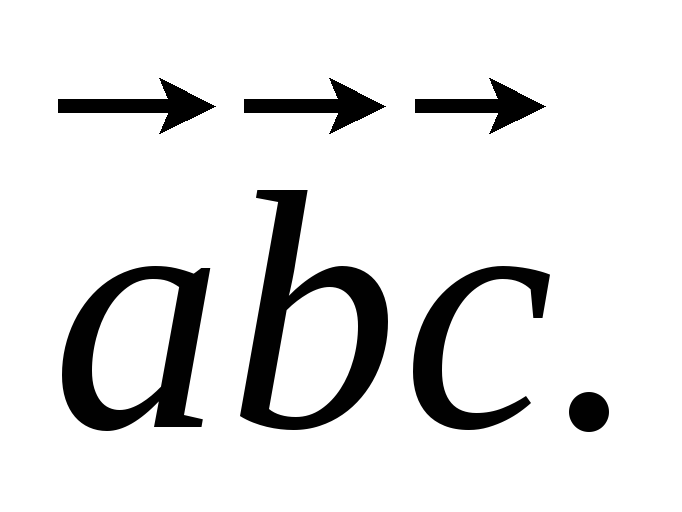
Доказать тождество
 .
.Вычислить объем тетраэдра с вершинами в точках
 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины на
грань
на
грань .
Если координаты его вершин имеют
координаты:
.
Если координаты его вершин имеют
координаты: ,
, .
.Доказать, что векторы
 и
и лежат
в одной плоскости.
лежат
в одной плоскости.Вычислить объем параллелепипеда, вершины которого находятся в точках
 ,
, ,
,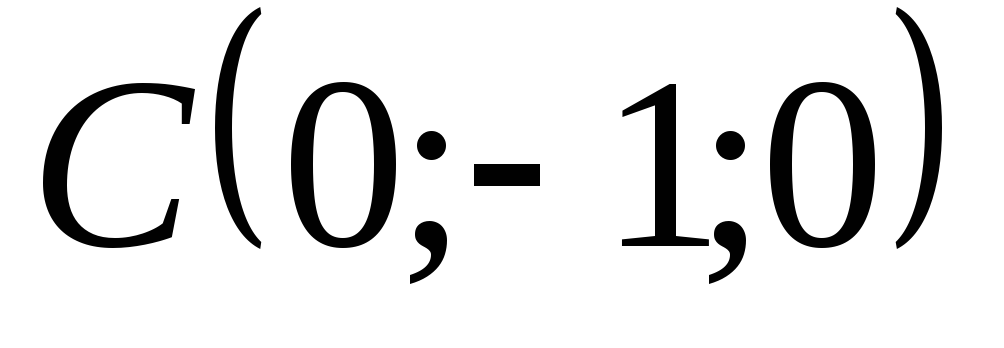 и
и .
.Вычислить объем тетраэдра с вершинами в точках
 ,
, ,
, и
и .
.На оси абсцисс найти точку, отстоящую на расстоянии
 от
точки
от
точки .
.Даны три вершины параллелограмма
 ,
, ,
, .
Определить четвертую вершину
.
Определить четвертую вершину
 .
.Определить координаты концов
 и
и отрезка, который точками
отрезка, который точками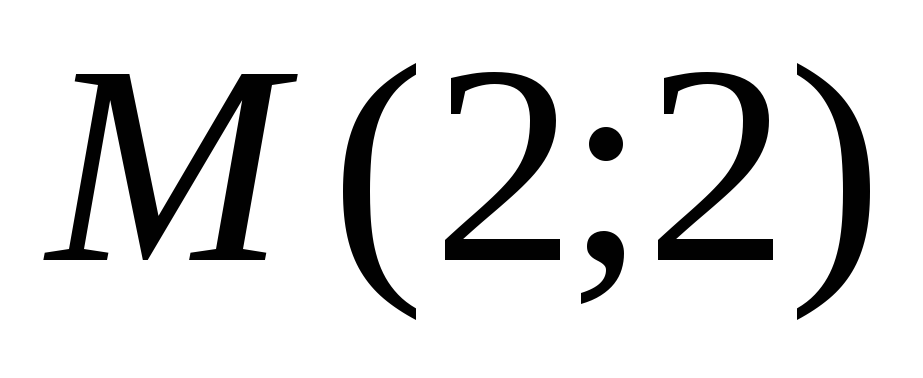 и
и разделен на три равные части.
разделен на три равные части.Прямая проходит через точки
 и
и .
Найти точки пересечения этой прямой с
осями координат.
.
Найти точки пересечения этой прямой с
осями координат.Составить уравнение прямых, проходящих через точку
 параллельно осям координат.
параллельно осям координат.Написать уравнение линии, каждая точка которой отстоит от прямой
 на расстоянии, в три раза большем, чем
от точки
на расстоянии, в три раза большем, чем
от точки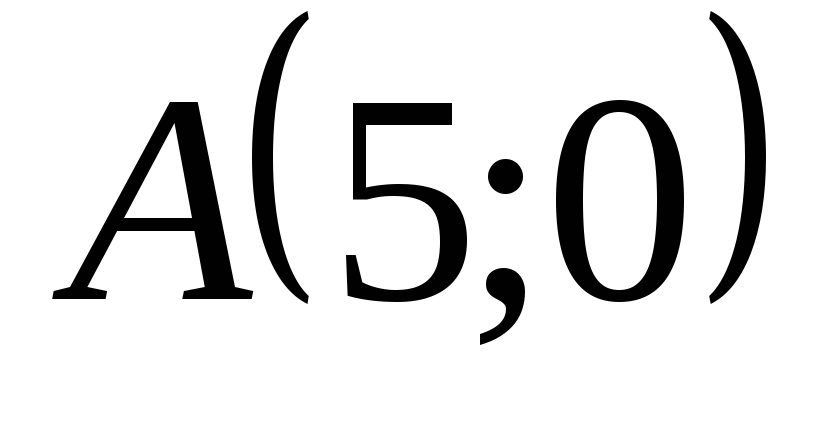 .
.Составить уравнение линии, каждая точка которой отстоит
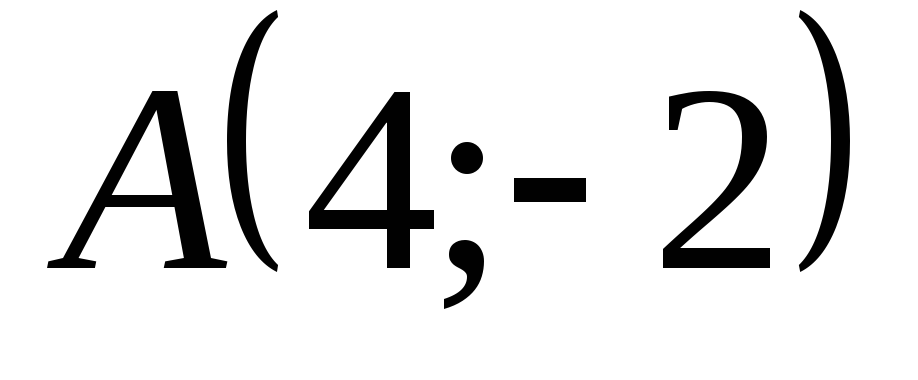 на расстоянии, в два раза меньшем, чем
от точки
на расстоянии, в два раза меньшем, чем
от точки .
.Найти уравнение геометрического места точек, одинаково удаленных от координатных осей.
Написать уравнение геометрического места точек плоскости, для которых отношение расстояний до точек
 и
и равно
равно .
.Написать уравнение геометрического места точек плоскости, сумма квадратов расстояний которых до точек
 и
и равна
31.
равна
31.Определить угловой коэффициент
 и отрезок
и отрезок ,
отсекаемый на
,
отсекаемый на для каждой из прямых:
для каждой из прямых:
1)
![]() ; 2)
; 2)![]() ;
3)
;
3)![]() ;
;
4)
![]() ;
5)
;
5)![]()
Дана прямая
 .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку :1)
параллельно данной прямой; 2) перпендикулярно
к данной прямой.
:1)
параллельно данной прямой; 2) перпендикулярно
к данной прямой.Составить уравнения прямых, проходящих через вершины треугольника
 ,
, и
и параллельно противоположным сторонам.
параллельно противоположным сторонам.Даны середины сторон треугольника
 ,
,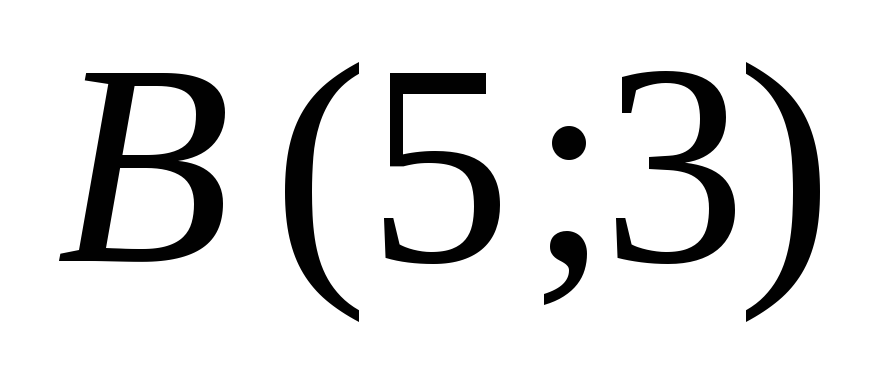 и
и .
Составить уравнения его сторон.
.
Составить уравнения его сторон.Даны вершины треугольника
 ,
, и
и .
Составить уравнения его высот.
.
Составить уравнения его высот.Даны вершины треугольника
 ,
, и
и .
Составить уравнение перпендикуляра,
опущенного из вершины
.
Составить уравнение перпендикуляра,
опущенного из вершины на медиану, проведенную из вершины
на медиану, проведенную из вершины .
.Даны уравнения двух смежных сторон параллелограмма
 и
и .
Составить уравнения двух других сторон,
если известна точка пересечения его
диагоналей
.
Составить уравнения двух других сторон,
если известна точка пересечения его
диагоналей .
.Составить уравнения катетов прямоугольного треугольника, зная уравнение гипотенузы
 и
вершину прямого угла
и
вершину прямого угла
Составить уравнение прямой, проходящей через точку
 на одинаковых расстояниях от точек
на одинаковых расстояниях от точек и
и .
.Определить угол между прямыми:
1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,
![]() ;
3)
;
3)
![]() ,
,![]() .
.
Даны две противоположные вершины квадрата
 и
и .
Составить уравнения его сторон.
.
Составить уравнения его сторон.Составить уравнения сторон треугольника, зная одну его вершину
 ,
а также уравнения биссектрисы
,
а также уравнения биссектрисы и медианы
и медианы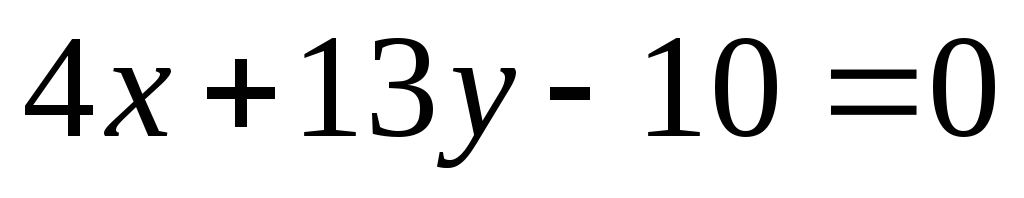 ,
проведенных из одной вершины.
,
проведенных из одной вершины.Уравнение одной из сторон некоторого угла
 ,
а уравнение биссектрисы
,
а уравнение биссектрисы .
Составить уравнение второй стороны
угла.
.
Составить уравнение второй стороны
угла.Вычислить расстояния от начала координат
 до точек:
до точек:
 и
и ,
, .
.Даны вершины треугольника:
 ,
, и
и .
Вычислить длину его медианы, проведенной
из вершиныА.
.
Вычислить длину его медианы, проведенной
из вершиныА.Составить уравнение плоскости, которая проходит через точку
 и
имеет нормальный вектор
и
имеет нормальный вектор
Даны две точки
 ,
, .
Составить уравнение плоскости, проходящей
через точкуА
перпендикулярно вектору
.
Составить уравнение плоскости, проходящей
через точкуА
перпендикулярно вектору
 .
.Составить уравнение плоскости
 ,
проходящей через точку параллельно
двум векторам
,
проходящей через точку параллельно
двум векторам и
и
Составить уравнение плоскости, проходящей через точки
 и
параллельно вектору
и
параллельно вектору
Составить уравнение плоскости, проходящей через три точки:
 .
.Составить уравнение плоскости, проходящей через прямую
 и точку
и точку .
.Составить уравнение плоскости, проходящей через две параллельные прямые
 и
и .
.Составить уравнение плоскости, проходящей через прямую пересечения плоскостей
 параллельно
вектору
параллельно
вектору
Составить уравнение плоскости, проходящей через прямую
 ,
перпендикулярно плоскости
,
перпендикулярно плоскости .
.Из точки
 опущен на плоскость перпендикуляр; его
основание
опущен на плоскость перпендикуляр; его
основание .
Составить уравнение плоскости.
.
Составить уравнение плоскости.Определить пары параллельных и перпендикулярных плоскостей:
1)
![]() ,
,![]() ;
2)
;
2)![]() ,
,
![]() ;
3)
;
3)
![]() ,
,![]() ;
;
4)
![]() ,
,![]() .
.
Составить уравнение плоскости, проходящей через точку
 параллельно плоскости
параллельно плоскости .
.Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям:
![]() ,
,
![]()
Составить уравнение плоскости, которая проходит:
через точку
 параллельно плоскости
параллельно плоскости
через точку
 параллельно плоскости
параллельно плоскости
через точку
 параллельно плоскости
параллельно плоскости
Составить уравнение плоскости, которая проходит:
через ось
 и точку
и точку ;
;через ось
 и точку
и точку ;
;через ось
 и точку
и точку .
.
Найти угол между плоскостями 1)
 ,
, ;
;
2)
![]() ,
,![]() ;
;
3)
![]() ,
,![]()
Написать уравнение плоскости, проходящей через точку
 перпендикулярно
вектору
перпендикулярно
вектору .
.
1)
![]()
2)
![]()
3)
![]()
Определить, при каком значении
 прямая
прямая
![]() пересекает:
1)
пересекает:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Составить канонические и параметрические уравнения прямых:
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() .
.
Составить уравнения прямой, проходящей через точку
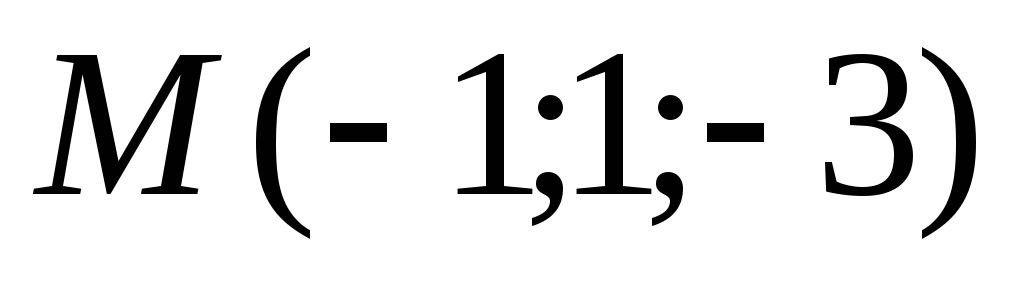 параллельно вектору
параллельно вектору .
.Составить уравнения прямой, проходящей через точки
 и
и .
.Составить уравнения прямой, проходящей через точку
 и образующей с осями координат углы
и образующей с осями координат углы
Составить уравнение прямой, проходящей через точку
 параллельно прямой
параллельно прямой
Составить уравнение прямой, проходящей через точку
 перпендикулярно плоскости
перпендикулярно плоскости
Написать канонические уравнения прямой, заданной как линия пересечения двух плоскостей.
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() .
.
Найти точку пересечения прямой и плоскости.
1)
![]() ,
,![]()
2)
![]() ,
,![]()
3)
![]() ,
,![]()
Найти координаты проекции точки
 на
плоскость:
на
плоскость:
1)
![]()
![]()
2)
![]()
![]()
3)
![]()
![]()
Найти координаты точки, симметричной точке
 относительно заданной прямой.
относительно заданной прямой.
1)
![]()
![]() .
.
2)
![]()
![]() .
.
3)
![]()
![]() .
.
Установить взаимное расположение прямой и плоскости и в случае их пересечения найти координаты точки пресечения:
1)
![]() и
и![]() ;
;
2)
![]() и
и![]() ;
;
Найти расстояние от точки
 до плоскости, проходящей через точки
до плоскости, проходящей через точки .
.
1)
![]()
![]()
2)
![]()
![]()
3)
![]()
![]()
Составить уравнение окружности в каждом из следующих случаев:
1) центр окружности
совпадает с началом координат и ее
радиус
![]()
2) центр окружности
совпадает с точкой
![]() и
ее радиус
и
ее радиус![]()
3)окружность
проходит через начало координат и ее
центр совпадает с точкой
![]() ;
;
4)окружность
проходит через точку
![]() и
ее центр совпадает с точкой
и
ее центр совпадает с точкой![]() ;
;
5)точки![]() и
и![]() являются концами одного из диаметров
окружности;
являются концами одного из диаметров
окружности;
6)центр окружности
совпадает с началом координат и прямая
![]() является касательной к окружности;
является касательной к окружности;
7)окружность
проходит через точки
![]() ,
а ее центр лежит на прямой
,
а ее центр лежит на прямой![]() ;
;
8)окружность
проходит через три точки
![]() и
и![]()
Написать уравнения окружностей, касающихся трех прямых:

 и
и .
.Составить уравнение диаметра окружности
 ,
перпендикулярно к прямой
,
перпендикулярно к прямой
Вычислить кратчайшее расстояние от точки
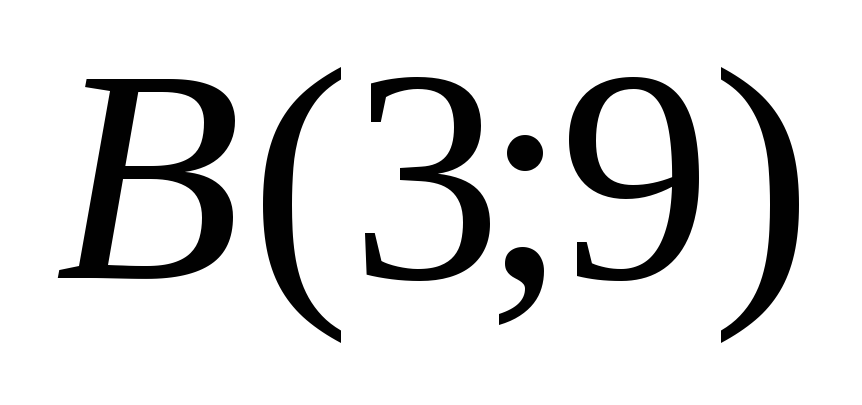 до окружности
до окружности
Окружности заданы уравнениями в декартовых прямоугольных координатах 1)
 2)
2) 3)
3) 4)
4) Составить
уравнения этих окружностей в полярных
координатах, при условии, что полярная
ось совпадает с положительной полуосью
Составить
уравнения этих окружностей в полярных
координатах, при условии, что полярная
ось совпадает с положительной полуосью ,
а полюс – с началом координат.
,
а полюс – с началом координат.Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:
его полуоси равны 5 и 2;
его большая ось равна 10, а расстояние между фокусами

его малая ось равна 24, а расстояние между фокусами

расстояние между его фокусами
 и
эксцентриситет
и
эксцентриситет
его большая ось равна 20, а эксцентриситет

его малая ось равна 10, а эксцентриситет

расстояние между его директрисами равно 5 и расстояние между фокусами

его большая ось равна 8, а расстояние между директрисами равно 16;
его малая ось равна 6, а расстояние между директрисами равно 13;
расстояние между его директрисами равно 32 и

Эксцентриситет эллипса
 ,
фокальный радиус точкиМ
эллипса
равен 10.
Вычислить
расстояние от точки
,
фокальный радиус точкиМ
эллипса
равен 10.
Вычислить
расстояние от точки
 до
односторонней с этим фокусом директрисы.
до
односторонней с этим фокусом директрисы.Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу
 и его малая полуось
и его малая полуось
Из точки
 проведены касательные к эллипсу
проведены касательные к эллипсу .
Вычислить уравнение хорды, соединяющей
точки касания.
.
Вычислить уравнение хорды, соединяющей
точки касания.Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:
ее оси
 и
и
расстояние между фокусами
 и
ось
и
ось
расстояние между фокусами
 и
эксцентриситет
и
эксцентриситет
ось
 и эксцентриситет
и эксцентриситет
уравнения асимптот
 и
расстояние между фокусами
и
расстояние между фокусами
расстояние между директрисами равно 22
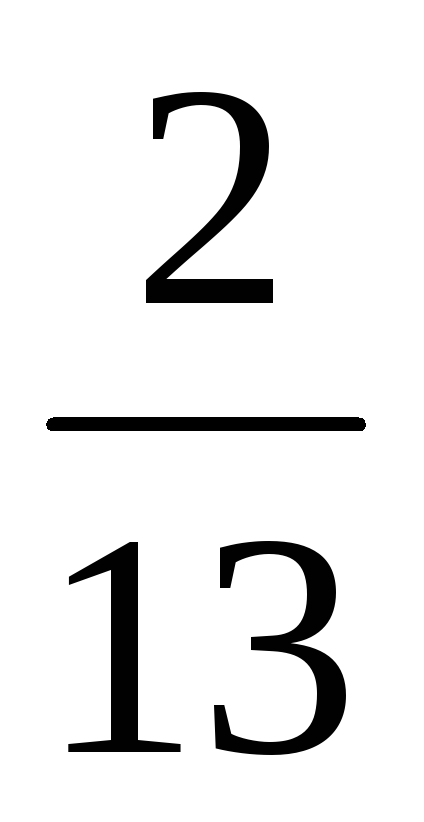 и расстояние между фокусами
и расстояние между фокусами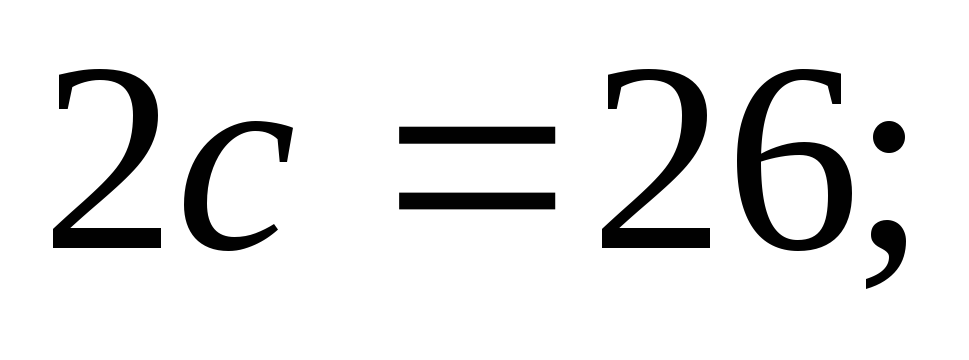
расстояние между директрисами
 и
ось
и
ось
расстояние между директрисами равно
 и
эксцентриситет
и
эксцентриситет
уравнение асимптот
 и
расстояние между директрисами равно
и
расстояние между директрисами равно
Определить точки гиперболы
 ,
расстояние которых до левого фокуса
равно 7.
,
расстояние которых до левого фокуса
равно 7.Найти точки пересечения прямой
 и гиперболы
и гиперболы
Провести касательные к гиперболе
 параллельно
прямой
параллельно
прямой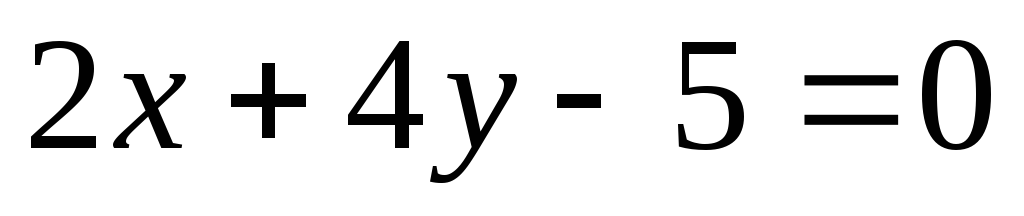 и
вычислить расстояние между ними.
и
вычислить расстояние между ними.На гиперболе
 найти точкуМ
ближайшую к прямой
найти точкуМ
ближайшую к прямой
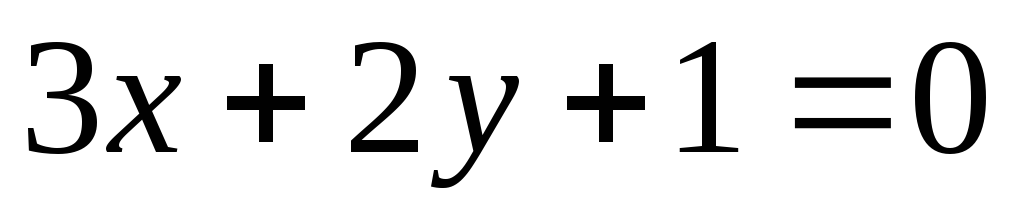 ,
и вычислить расстояние от этой точки
до этой прямой.
,
и вычислить расстояние от этой точки
до этой прямой.Определить эксцентриситет гиперболы, если отрезок между ее вершинами виден из фокусов сопряженной гиперболы под углом в
 .
.Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
парабола расположена симметрично относительно оси
 и
проходит через точку
и
проходит через точку
парабола расположена симметрично относительно оси
 и
проходит через точку
и
проходит через точку
парабола расположена симметрично относительно оси
 и
проходит через точку
и
проходит через точку
парабола расположена симметрично относительно оси
 и
проходит через точку
и
проходит через точку
Составить уравнение параболы, если ее даны ее фокус
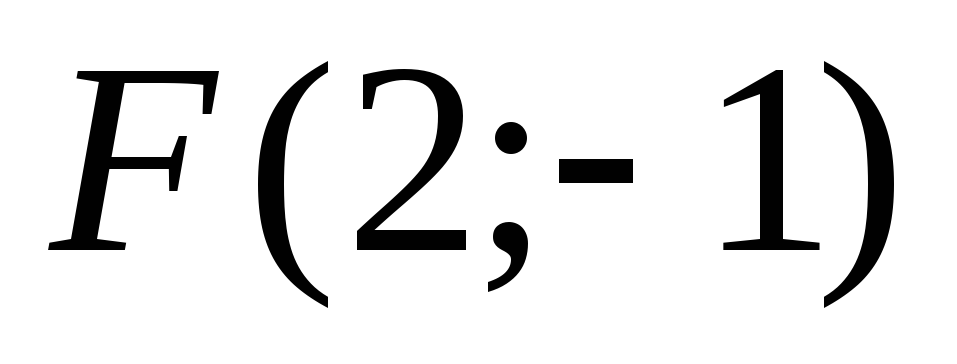 и
директриса
и
директриса .
.Определить точки пересечения прямой
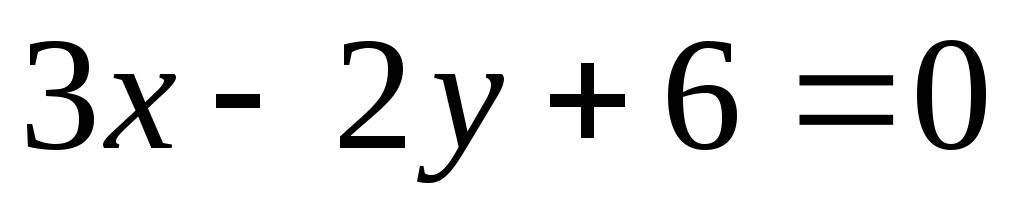 и
параболы
и
параболы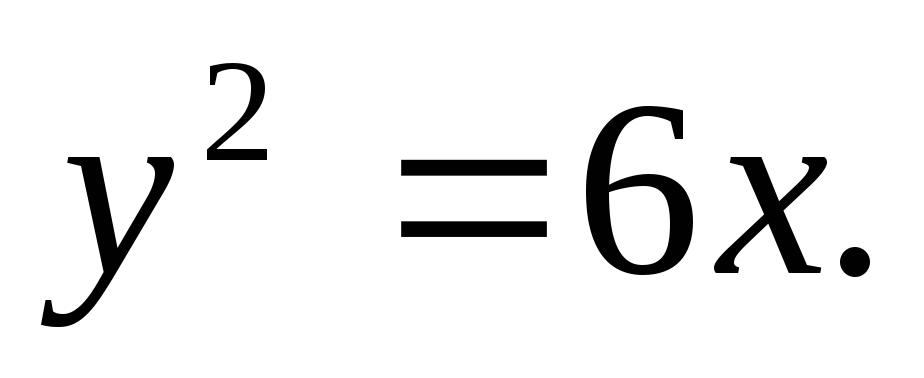
Составить уравнения касательных к параболе
 ,
проведенных из точки
,
проведенных из точки
Ответы
3.
3. 4.
9. 5.
![]() .6.
.6.
![]() 7.
7.
![]() .8.
.8.
![]() .
.
9.
![]() .10.
.10.
![]() .11.
1) да; 2) да. 12.
.11.
1) да; 2) да. 12.
![]() .
.
13.
![]() .14.
–6. 15.
–4. 16.
.14.
–6. 15.
–4. 16.
![]() .
.
17.
1)
![]() ;
2)
;
2)![]() .
.
18.
1) 9; 2) 16; 3) 13; 4) 37; 5) –61. 19.
![]() .20.
.20.
![]() .
.
21.
![]() .22.
.22.
![]() .23.
1)
.23.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .24.
.24.
![]() .25.
12. 26.
1)
.25.
12. 26.
1)
![]() ;
2)
;
2)![]() .27.
.27.
![]() .
.
28.
![]() .29.
1. 30.
1) да; 2) нет. 31.
1) нет; 2) да.
.29.
1. 30.
1) да; 2) нет. 31.
1) нет; 2) да.
32.
![]() ;
знак плюс в случае, когда тройка векторов
;
знак плюс в случае, когда тройка векторов![]() правая, минус – когда эта тройка левая.
правая, минус – когда эта тройка левая.
33. 34.
![]() .35. 36.
1084. 37.
.35. 36.
1084. 37.
![]() .38.
.38.
![]() .39.
.39.
![]()
40.
![]() .41.
.41.
![]() .42.
.42.
![]() .
.
43.
 .44.
.44.
![]() .
.
45.
![]() .46.
.46.
![]() .
.
47.
![]() .48.
1)
.48.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() .
.
49.
1)
![]() 2)
2)![]() .
.
50.
![]() .
.
51.
![]() .
.
52.
![]() .
.
53.
![]() .54.
.54.
![]() .
.
55.
![]() .
.
56.
![]() .57.
1)
.57.
1)
![]() 2)
2)
58.
![]() .
.
59.
![]() .
.
60.
![]() .61.
.61.
![]() .
.
62.
7. 63.
![]() .64.
.64.
![]() .
.
65.
![]() .66.
.66.
![]() .
.
67.
![]() .68.
.68.
![]() .69.
.69.
![]() .
.
70.
![]() .71.
.71.
![]() .
.
72.
![]() .73.
параллельны: 1); 4). Перпендикулярны: 2).
74.
.73.
параллельны: 1); 4). Перпендикулярны: 2).
74.
![]() .75.
.75.
![]() .
.
76.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
77.
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
78.
1)
![]() ;
2) 0; 3)
;
2) 0; 3)![]() .
.
79.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
80. 1) –4 2) 9; 3) 3.
81.
1)
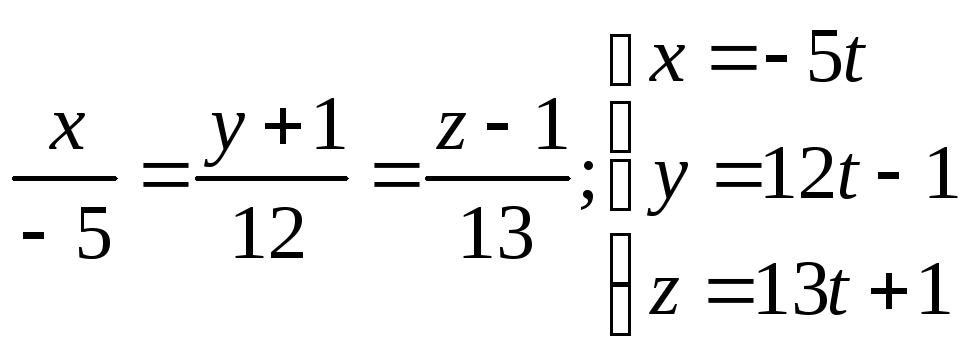 ;
2)
;
2)![]()
 ;
3)
;
3) .82.
.82.
![]() .
.
83.
![]() .84.
.84.
![]()
85.
![]() .86.
.86.
![]() .
.
87.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
88.
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
89.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
90.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
91. 1), 2) прямая и плоскость параллельны.
92.
1)
![]() ;
2)
;
2)![]() ;
3) 0.
;
3) 0.
93.
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() .
.
94.
![]() и
и![]() .
.
95.
![]() .96.
17.
.96.
17.
97.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
98.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
;
9)
![]() или
или ;
10)
;
10)![]() .99.
15.
.99.
15.
100.
![]() .101.
.101.
![]() .
.
102.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
;
9)
![]() .103.
.103.
![]() и
и![]() .104.
.104.
![]() и
и![]() .
.
105.
![]() .
.
106.
![]() .107.
.107.
![]() .
.
108.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
109.
![]() .
.
110. прямая и парабола не пересекаются.
111.![]() и
и![]() .
.
