Астраханский Государственный Технический Университет

Кафедра «Математика в инженерном образовании»

Линейная алгебра

Векторная алгебра

Аналитическая геометрия

Введение в математический анализ

Учебно-методическое пособие

Часть I

Астрахань 2008г.

Автор:	старший преподаватель кафедры «Математика в инженерном образовании» Андреева Л.А. к.п.н., кафедры «Математика в инженерном образовании» Мамаева Н.А. ассистент кафедры «Математика в инженерном образовании» Агапова Ю.Б.
Рецензент:	к.т.н., доцент кафедры «Математика в инженерном образовании» Ключарев А.Ю.
Компьютерный набор:	Иванникова А.Н.

Учебное пособие рассмотрено и одобрено на заседании кафедры, протокол № 8 от 4.07.2008г.

Содержание

1.	Элементы линейной алгебры	4
2	Элементы векторной алгебры	40
3	Элементы аналитической геометрии	45
4	Предел функции. Непрерывность.	88
5	Производная и дифференциал функции	126
6	Исследование функции	164

§ 1. Элементы линейной алгебры.

1. Матрицы. Действия над матрицами.

Матрицей называется прямоугольная таблица чисел или буквенных выражений, содержащая – строк и– столбцов.

, где – элемент матрицы,– номер строки,– номер столбца.

Число строк столбцов матрицы называется ее размерностью и обозначается .

Если , матрица называется квадратной-го порядка.

Нулевой матрицей называется матрица, у которой все элементы равны нулю.

Единичной матрицей называется квадратная матрица, диагональные элементы которой равны единице, а остальные равны нулю.

–единичная матрица третьего порядка.

Суммой двух матриц иодинаковой размерности называется матрицатой же размерности, каждый член которой равен сумме соответствующих членов матрици.

, где ,,.

Пример 1.1.

Произведением матрицы на числоназывается матрицатой же размерности, каждый член которой равен произведению числана соответствующие элементы матрицы.

, где ,,.

Пример 1.2.

.

Произведением матрицы размерностина матрицуразмерностиназывается матрица, каждый член которой равен сумме парных произведений элементов-ой строки первой матрицы на элементы-го столбца второй матрицы.

, где

Пример 1.3.

.

Пример 1.4.

Найти матрицы , где,.

, ,

.

Пример 1.5.

Найти , где.

.

Пример 1.6.

Найти где.

.

, ,

.

2. Определители и их свойства.

Пусть дана матрица второго порядка

.

Определителем (детерминантом) второго порядка, соответствующим данной матрице , называется число получаемое следующим образом:

(1)

Пусть дана матрица третьего порядка

.

Определителем третьего порядка, соответствующим данной матрице , называется число получаемое следующим образом:

(2)

Минором данного элементаопределителя третьего порядка называется определитель второго порядка, получаемый из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.

Алгебраическим дополнением данного элемента называется его минор, взятый со знаком плюс, если сумма индексов четная и со знаком минус, если сумма индексов нечетная.

Свойства определителей.

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами.

2. При перестановке двух строк (столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.

3. определитель с двумя одинаковыми строками (столбцами) равен нулю.

4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

5. Определитель с двумя пропорциональными строками (столбцами) равен нулю.

6. Определитель не изменится, если к какой-либо строке (столбцу) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

7. Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.

Пример 1.7. Вычислить определитель второго порядка .

Решение.

.

Пример 1.8. вычислить определители третьего порядка .

Решение. I способ

По формуле (2)

.

II способ. Используя свойство 3, преобразуем определитель следующим образом. Сначала умножим первую строку на 3 и сложим со второй, результат запишем во второй строке. Затем первую строку умножим на 2 и сложим с третьей, результат запишем в третьей строке.

Теперь разложим определитель по элементам второго столбца

.

3. Решение систем линейных уравнений методом Крамера.

Рассмотрим систему трех линейных уравнений с тремя неизвестными

(1)

Тройка чисел называется решением системы (1), если при подстановке этих чисел вместовсе три уравнения обращаются в верные тождества.

Назовем определитель составленный из коэффициентов при неизвестных главным и обозначим . Таким образом,.

Определители при неизвестных получаются из главного путем замены соответствующего столбца коэффициентов прина столбец свободных членов, т.е.

.

Если главный определитель системы (1) , то система имеет единственное решение

. (2)

Формулы (2) называются формулами Крамера.

Пример 1.9.

Решить систему уравнений по формулам Крамера.

Решение.

Вычисляем определители

.

По формулам (2) находим .

Ответ: .

Если определитель системы и хотя бы один из определителей,не равен нулю, то система не имеет решений.

Если и, то система либо не имеет решений, либо имеет бесчисленное множество решений.

Пример 1.10.

Решение.

Данная система имеет определители

Умножим первое уравнение на 3 и вычтем из него третье уравнение, получим невозможное равенство . Следовательно, система не имеет решений.

Пример 1.11.

Решение.

Данная система имеет определители .

Рассмотрим подсистему, состоящую из двух первых уравнений

или

Решим последнюю систему по формулам Крамера

,

,

.

Пусть , тогда.

Таким образом, система имеет множество решений: ,.

Однородная система уравнений имеет вид

Если ее главный определитель , то система имеет единственное решение.

Если главный определитель , то однородная система имеет бесчисленное множество решений.

Пример 1.12.

Решить систему уравнений

Решение.

Вычислим главный определитель

.

Так как , то система имеет единственное решение.

Пример 1.13.

Решить систему уравнений.

Решение:

Находим главный определитель

Следовательно, система имеет ненулевое решение.

Составим подсистему уравнений

или

,

,

.

По формулам (2) находим .

Система имеет множество решений .

4. Решение систем линейных уравнений методом Гаусса (метод последовательного исключения неизвестных).

Покажем этот метод на примерах.

Пример 1.14.

Решить систему уравнений

Решение:

Составим расширенную матрицы системы и с помощью элементарных преобразований преобразуем ее к диагональному виду (элементы под главной диагональю равны нулю)

Умножим первую строку на (-2) и сложим со второй; затем умножим первую строку на (-3) и сложим с третьей.

Умножим вторую строку на и сложим с третьей

Теперь для полученной матрицы составим систему уравнений и решим ее

Ответ: .

Пример 1.15.

Решить систему уравнений

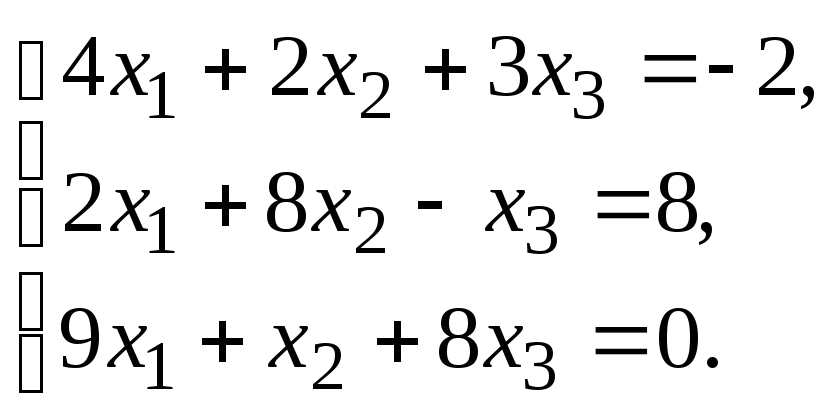
Решение.

Составим расширенную матрицу

. Полученной матрице соответствует система

при каких значениях . Следовательно, система уравнений несовместна.