8. Схема исследования функции.

1. Найти область определения функции.

2. Исследовать функцию на четность (нечетность).

3. Исследовать функцию на непрерывность. Найти точки разрыва, вертикальные и наклонные асимптоты.

4. Найти нули функции, интервалы, знакопостоянства, точки пересечения графика с осью .

5. Найти интервалы возрастания и убывания функции и её экстремумы.

6. Найти интервалы выпуклости и вогнутости графики функции и её точки перегиба.

7. Используя полученные данные, построить график функции.

Пример 6.7. Исследовать функцию и построить её график: ;

Решение:

1) Область определения функции .

2) , т.е., функция нечетная и её график симметричен относительно начала координат.

3) Функция непрерывна, точек разрыва нет, вертикальных асимптот нет.

Наклонная асимптота не существует, т.к.

.

4) Найдем нули функции:

.

Интервалы знакопостоянства:

Значит, при,

при .

5) Найдем производную: .

–критические точки.

Определим знак производной в интервалах .

Следовательно, функция возрастает на интервалах , убывает на интервале.

–точка максимума, ;

–точка минимума, .

6) Найдем вторую производную: при.

При , следовательно, график функции вогнутый на интервале.

При , следовательно график функции выпуклый на интервале.

Точка – точка перегиба графика,.

Строим график функции.

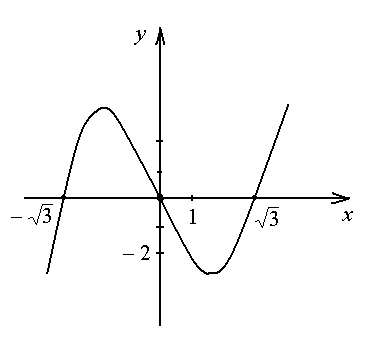
Пример 6.8. Исследовать функцию и построить её график

.

Решение.

1) Область определения функции: .

2) и, функция общего вида.

3) Функция непрерывна на интервале . В точкефункция имеет разрыв.

,

.

Поэтому – вертикальная асимптота.

Найдем наклонную асимптоту .

.

.

–наклонная асимптота

4) Нули функции: .

Интервалы знакопостоянства: .

Итак, при,при.

5) Найдем производную:

.

Откуда и– критическая точка.

Определим знак производной в интервалах ,.

Функция возрастает на интервалах и убывает на интервале– точка максимума,. В точкеэкстремума нет, т.к. производная не меняет знак при переходе через.

6) Найдем вторую производную:

.

при

Определим знак второй производной: при. Следовательно, график функции в интервалевогнутый.

при . Следовательно, график функции в интервалевыпуклый.

Точка – точка перегиба,.

Строим график функций.

9. Наибольшее и наименьшее значения функции

Для отыскания наибольшего и наименьшего значений функции, непрерывной на некотором отрезке , надо вычислить значения этой функции на концах отрезка и во всех критических точках, принадлежащих этому отрезку. Наибольшее и наименьшее из полученных чисел и будет соответственно наибольшим и наименьшим значениями функции на отрезке.

Пример 6.9. Найти наибольшее и наименьшее значения функции

на отрезке .

Решение.

Найдем производную и критические точки:при,при. Критическая точкане принадлежит отрезку.

Найдем значения функции: .

Итак, наибольшее значение , наименьшее значение.

Пример 6.10. Бак цилиндрической формы (с крышкой) должен вмещать л воды. Каковы должны быть размеры бака, чтобы на его изготовление пошло меньше материала?

Решение:

Известна формула площади полной поверхности цилиндра

. Согласно условию задачи, объем цилиндра , откуда.

Следовательно, .

Исследуем функцию на наименьшее значение при.

.

Далее, . Таким образом, вторая производная в критической точкеположительна. Следовательно, по правилу 2 функцияимеет в точкеминимум. Этот минимум является её наименьшим значением, т.к.непрерывна в интервалеи имеет только один экстремум – минимум.