§ 4. Предел функции. Непрерывность.

Число называется пределом функциипри, если для любого наперед заданного положительногосуществует такая– окрестность точки, что для всехиз– окрестности и, быть может, выполняется неравенствои пишут.

При вычислении пределов функций используют следующие свойства пределов:

1. ;

2. .

Если существует предел функций ипри, то

3. ;

4. ;

5. ;

6. .

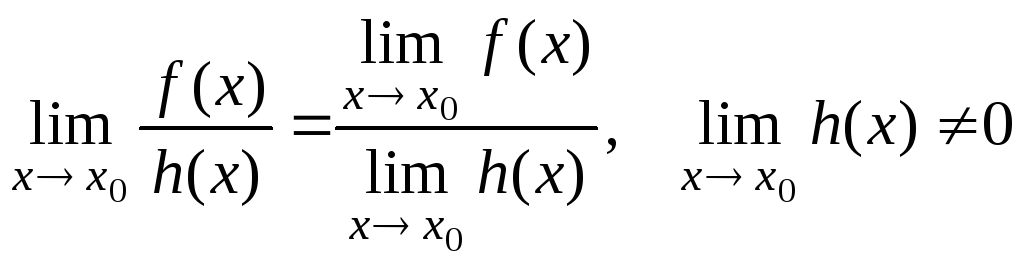Функция называется непрерывной в точке, если:

1) она определена в точке и некоторой ее окрестности; 2) существует предел функций, в этой точке т.е.; 3) предел функции в точкеравен значению функции в точке, т.е..

Для основных элементарных функций в любой точке их области определения имеет место равенство: , т.е. предел находят непосредственной подстановкой предельного значения аргумента.

Функция называется непрерывной в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е..

Пример 4.1. Доказать, что .

Решение. Рассмотрим абсолютную величину разности

.

Покажем, что выражение может быть меньше любого наперед заданного положительного бесконечно малого числа. Для этого решим неравенство, отсюда.

Это неравенство выполняется при условии или. Решая два неравенства, получимили. Следовательно, дляфункция будет отличаться от своего предела меньше чем на. Поэтому.

Найти пределы

Пример 4.2. .

Решение.

.

Пример 4.3. .

Решение.

Неопределенность раскрывается методом разложения числителя и знаменателя на линейные множители с последующим сокращением дроби на множитель.

.

Пример 4.4. .

Решение.

Неопределенность раскрывается методом умножения числителя и знаменателя на выражение сопряженное числителю.

Пример 4.5. .

Решение.

.

Неопределенность раскрывается методом деления числителя и знаменателя дроби на наибольшую степень.

.

Пример 4.6. .

Решение.

.

Пример 4.7. .

Решение.

Пусть и– бесконечно малые функции при, т.е.,.

Если , тоиназываются эквивалентными бесконечно малыми функциями и обозначаются.

;

;

;

.

;

;

;

.

Пример 4.8. .

Решение.

Так как при, то

.

Пример 4.9. .

Решение.

Так как при,то

.

Пусть функция . Если прии, то имеем неопределенность.

Для раскрытия неопределенности используются формулы

или (1)

(2)

называемые вторым замечательным пределом.

Пример 4.10. .

Решение.

Имеем неопределенность вида . Преобразуем выражение под знаком предела так, чтобы можно было применить формулу (1)

,

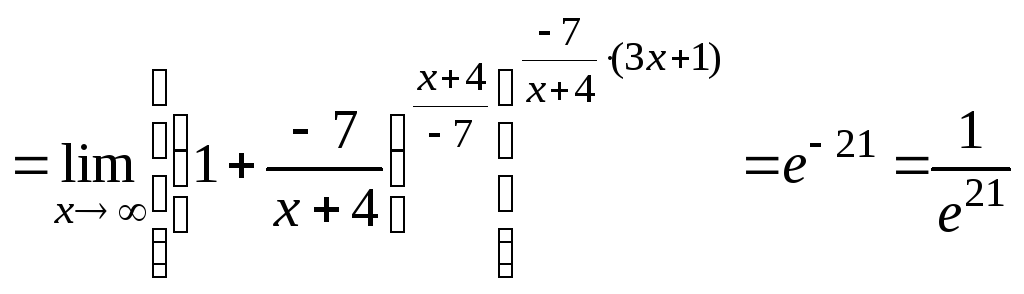т.к. .

Пример 4.11. .

Решение.

Имеем неопределенность вида . Применим формулу (2).

.

Пример 4.12. .

Решение.

Имеем неопределенность вида . Применим формулу (2).

.

Пример 4.13. .

Решение.

Имеем неопределенность . Обозначим. Если, то.

.

Пример 4.14. Доказать, что функция – непрерывна.

Решение.

Функция определена в интервале.Дадим аргументу в произвольной точкеприращение, тогда и функция получит приращение:.

Тогда

.

Известно, что ,

.

Таким образом, имеем произведение функции бесконечно малой на ограниченную, т.е. . Следовательно– непрерывна в интервале.

Пример 4.15. Исследовать на непрерывность и построить график функции

Так как функции непрерывны на интервале, то они непрерывны и в указанных интервалах. Следовательно, функциянепрерывна в интервалах,,. Исследуем точкина непрерывность.

Проверим выполнимость условий для .

1) ;

2) ;

;

3) .

Все условия выполняются, следовательно, – точка непрерывности.

Проверим выполнимость условий для .

1) ;

2) ,

, т.е. , следовательно,– точка разрываI рода. График функции имеет вид.

Пример 4.16. Найти точки разрыва функции .

Решение. Преобразуем знаменатель дроби:

. Очевидно, функция непрерывна при и. Исследуем точкии.

; .

Следовательно, – точка разрываII рода.

; .

Следовательно, – точка разрываII рода.

Пример 4.17. Исследовать функцию .

Решение.

Элементарная функция определена на всем множестве действительных чисел, кроме, следовательно, в этой точке функция имеет разрыв. Так как функция в точкеимеет предел:, то разрыв устранимый. Если эту функцию доопределить в точке, положив, то функция будет непрерывна на всем множестве действительных чисел.