2. Частотные характеристики систем первого порядка

Пример 2. Рассмотрим разностное уравнение системы первого порядка y(n) = x(n) + Кy(n – 1) (4)

с начальным условием y(–1) = 0. Можно установить, что импульсная характеристика системы первого порядка (4.4) равна

h(n)= (5)

Рис.2. Частотные характеристики систем первого порядка (4.4)

Используя формулу (2), найдем частотную характеристику си­стемы первого порядка (4) с импульсной характеристикой (5)

H(e^j)=.

Функцию H(e^j)можно представить в виде

H(e^j) = H(e^j),

где H(e^j)= 1 / ; arg H(e^j) =  – arctg .Графики lg|H(e^j)| и argH(e^j) для различных значений K приведены на рис. 2. Функция H(e^j) здесь – характе­ристика фильтра нижних частот. Характеристики H(e^j) и argH(e^j) могут быть получены из геометрических представлений.

3. Частотные характеристики систем второго порядка

Рассмотрим систему второго порядка, разностное уравнение которой имеет вид

y(n) = x(n) + а₁ y(n – 1) + а₂ y(n – 2) (6)

– частный случай уравнения (3.5).

В общем случае уравнение второго порядка содержит также чле­ны вида b₁x(n – 1) и b₂x(n – 2), однако для простоты изложения эти члены опущены. При нулевых начальных усло­виях y(–1) = 0 и y(–2) = 0 нетрудно показать, что, если корни однородного уравнения не совпадают, то импульс­ная характеристика системы может принять одну из двух форм:

h(n) = ₁ + ₂ (I), (7)

где p₁ и p₂ – действительные числа, либо

h(n) = ₁r ⁿ sin(bn + ) (II). (8)

Импульсная характеристика (7) описывает две системы первого порядка.

Выражение (8) описы­вает систему второго порядка, импульсная характеристика кото­рой – затухающая синусоида. Импульсная характери­стика имеет вид (8), когда коэффициенты разностного урав­нения (6) удовлетворяют условию, а₂ < –а₁²/4,из которого следует, что а₂ < 0.

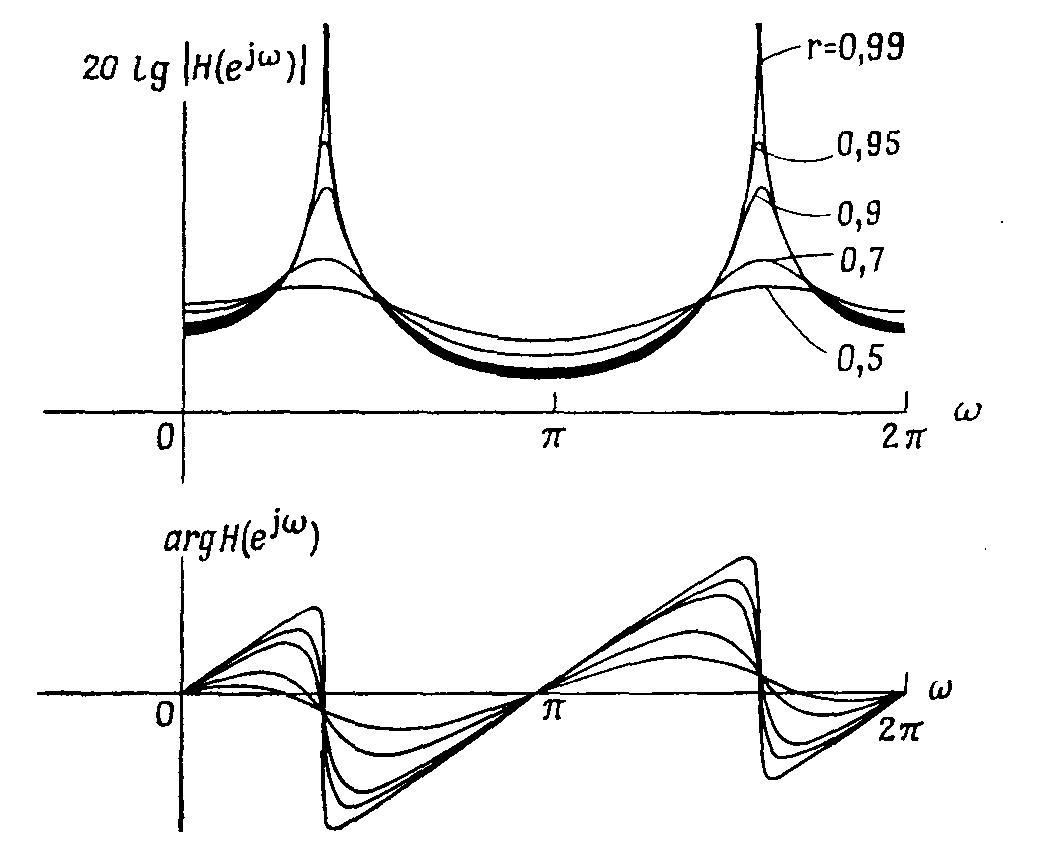
Рис. 3. Частотные характеристики систем второго порядка

Если условие а₂ < –а₁²/4 выполняется, то

r = ; cosb = а₁/ 2,  = b, ₁ = 1/ sinb.

Частотную характеристику, соответствующую импульсной ха­рактеристике (4.8), можно записать следующим образом:

H(e^j) = 1 / [1 – 2 r (cosb) e^–j + r²e^–2j.].

Амплитудные (в логарифмическом масштабе) и фазовые характе­ристики системы второго порядка, соответствующие фиксирован­ному значению b = /4 и различным значениям r, приведены на рис. 3 – система обладает резонансными свойствами.

Лекция 4

1. Дискретный ряд Фурье

Частотная характеристика дискретной системы – периодическая функция частоты , поэтому равенство (4.2)

H(e^j) = (1)

можно рассматривать как разложение функции H(e^j) в ряд Фурье, при­чем коэффициенты разложения – это отсчеты импульсной характеристики системы. Согласно теории рядов Фурье, коэффициенты h(n) могут быть выражены через H(e^j):

h(n) = H(e^j) e^jnd. (2)

Равенства (4.2), (1) и (2) представляют собой пару преобразований Фурье. Из соотношения (2) видно, что h(n) по существу – суперпозиция синусоид е^jn = cos(n) + j sin(n) с ам­плитудами H(e^jn). Пара преобразований (1) и (2) справед­лива для любой последовательности с конечной суммой (1), поэтому произвольную входную последовательность также можно представить в виде

x(n) = X(e^j) e^jnd. (3)

где X(e^j) =. (4) Согласно формулам (4.1)

y(п) = = e^{j n}= x(п) H(e^j ),

отклик на последовательность e^jn равен H(e^j)e^jn, поэтому откликом на входную последо­вательность (5.3) будет

y(n) = X(e^j) H(e^j) e^jnd. (5)

– для суммирования откликов использовано свойство линейности системы.

Из равенства Y(e^j)= X(e^j) H(e^j)

нетрудно увидеть, что (5.5) – одно из двух соотношений, представляющих собой пару преобразований Фурье для последо­вательности y(n).

Таким образом, показано, что и для дискрет­ных систем свертка во временной области соответствует умноже­нию в частотной области. Итак, частотная характеристика H(e^j) представляет собой отклик системы на ограниченный класс вход­ных последовательностей вида

e^jn, 0  < 2.

Однако соотношение (5.3) показывает, что произвольные после­довательности – это суперпозиция таких экспонент, поэтому функция H(e^j) – важное средство описания отклика системы почти на любые входные последовательности.