27.3 Цифровые компараторы
Цифровые компараторы – это КЦУ, предназначенные для сравнения двух двоичных чисел.
Обычно компаратор имеет входы наращивания разрядности, куда подключаются выходы результатов сравнения от другого компаратора. Это позволяет увеличивать разрядность сравниваемых чисел. УГО типичного цифрового компаратора приведено на рисунке 27.4. Работу цифрового компаратора можно представить следующим словесным описанием:
– если число А больше числа В, то активный уровень присутствует на выходе «А>В»;
– если число А меньше числа В, то активный уровень присутствует на выходе «А<В»;
– если число А равно числу В, то активный уровень без изменения копируется с одного из входов результата сравнения («А>В», «А=В» или «А<В») на одноимённый выход. При этом активный уровень должен присутствовать только на одном из этих входов.
Рисунок 27.4 – УГО цифрового компаратора
Если используется одиночная микросхема, то для ее правильной работы достаточно подать единицу на вход A = B, а состояния входов A<B и A>B не важны, на них можно подать как нуль, так и единицу. Если микросхемы компараторов кодов каскадируются (объединяются) для увеличения числа разрядов сравниваемых кодов, то надо выходные сигналы микросхемы, обрабатывающей младшие разряды кода, подать на одноименные входы микросхемы, обрабатывающей старшие разряды кода (рисунок 27.5).
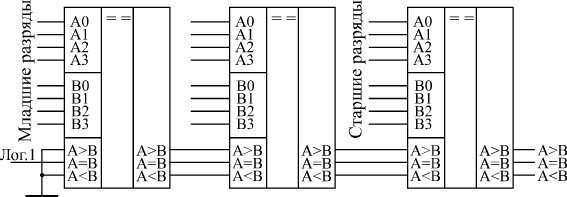
Рисунок 27.5 – Схема увеличения разрядности цифрового компаратора
Одно из основных применений компараторов кодов состоит в селектировании входных кодов. В этом случае достаточно иметь информацию только о совпадении кодов на входах компаратора, а не о соотношении их величин. Интересующий нас код (эталонный) подается на один вход компаратора, а изменяющийся код (входной) – на другой вход. Используется только выход равенства кодов А = В.
Микросхемы, выполняющие функции цифрового компаратора, кодируются буквами СП.
27.4 Схема проверки на чётность/нечётность
Схема проверки на чётность/нечётность – это КЦУ, сигнал на выходе которого будет активным, если количество единиц в поданном на вход двоичном наборе чётно/нечётно.
УГО типичной схемы проверки на чётность/нечётность приведено на рисунке 27.6. Описание работы схемы проверки на чётность/нечётность в таблице 27.3.
Наиболее важным применением схем проверки на четность/нечетность является проверка ситуации когда полученные с линии или извлеченные из памяти данные искажены ошибкой и использовать их нельзя. Общая схема организации контроля показана на рисунке 27.7.
Рисунок 27.6 – УГО Схемы проверки на четность/нечетность
Таблица 27.3 – Таблица истинности схемы проверки на четность/нечетность
|
Входы |
Выход чётности | |||
|
D0 |
D1 |
D2 |
D3 |
Q0 |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Рисунок 27.7 – Схема организации контроля линии связи
Работает представленная схема следующим образом. На n-входовом элементе формируется признак четности Р числа, который в качестве дополнительного (n+1)-го контрольного разряда (parity bit) отправляется вместе с передаваемым словом в линию связи или запоминающее устройство. Передаваемое (n+1)-разрядное слово имеет всегда нечетное число единиц. Если в исходном слове оно было нечетным, то функция от такого слова равна 0, и нулевое значение контрольного разряда не меняет числа единиц при передаче слова. Если же число единиц в исходном слове было четным, то контрольный разряд Р для такого числа будет равен 1 и результирующее число единиц в передаваемом (n+1)-разрядном слове станет нечетным. Вид контроля, когда по линии передается нечетное число единиц, по строгой терминологии называют контролем по нечетности.
На приемном конце линии или после чтения из памяти от полученного (n+1)-разрядного слова снова берется свертка по четности. Если значение этой свертки равно 1, то или в передаваемом слове, или в контрольном разряде при передаче или хранении произошла ошибка. Столь простой контроль не позволяет исправить ошибку, но он, по крайней мере, дает возможность при обнаружении ошибки исключить неверные данные, затребовать повторную передачу и т.д.
Контроль по четности – самый дешевый по аппаратурным затратам вид контроля, и применяется он очень широко. Практически любой канал передачи цифровых данных или запоминающее устройство, если они не имеют какого-либо более сильного метода контроля, защищены контролем по четности.
Микросхемы, выполняющие функции схемы проверки на чётность/нечётность кодируются буквами ИП.
Лекция № 28
СУММАТОРЫ