Решение.
Это уравнение
первого порядка является линейным, так
как это удовлетворяет общему виду
линейных уравнений
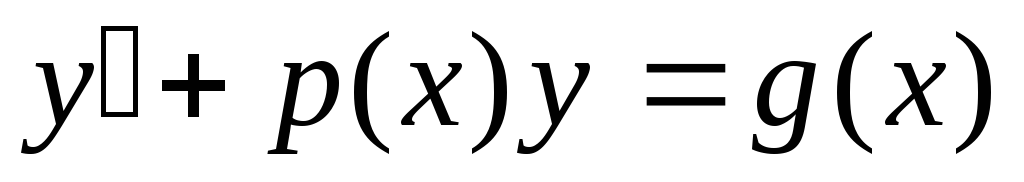 .
Будем искать решение в виде
.
Будем искать решение в виде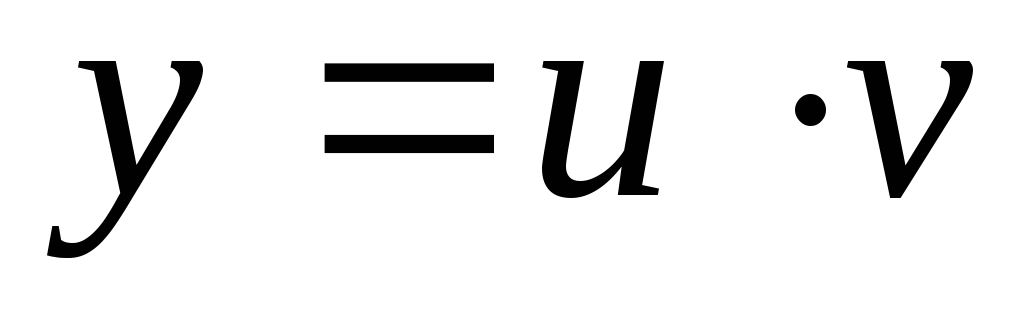 ,
где
,
где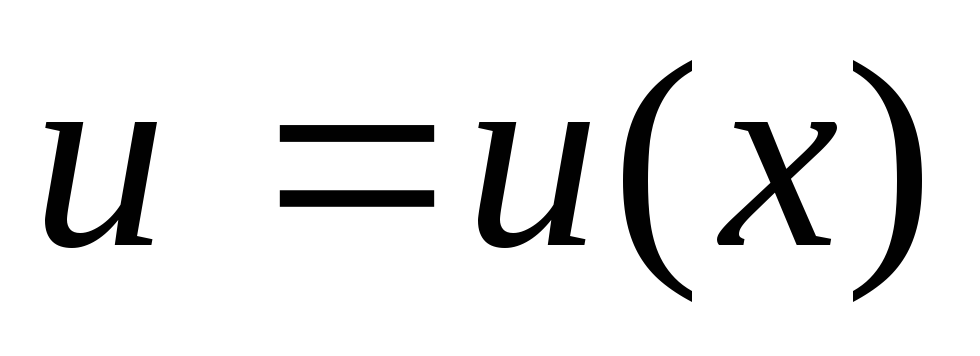 ,
,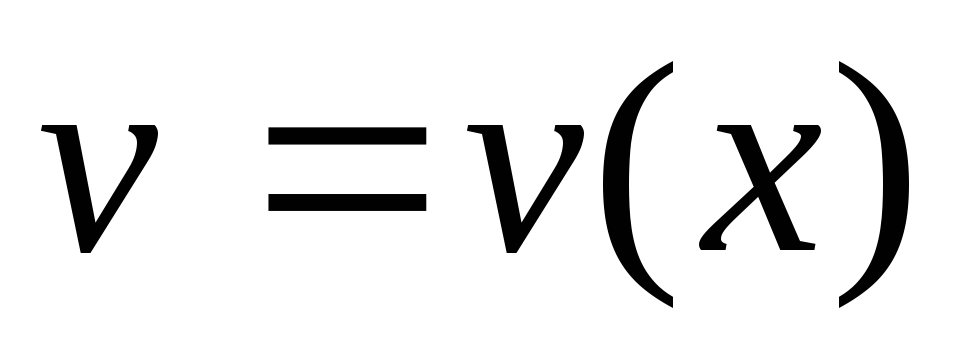 -
дифференцируемые функции от
-
дифференцируемые функции от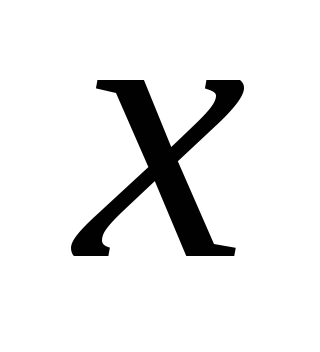 .
Тогда
.
Тогда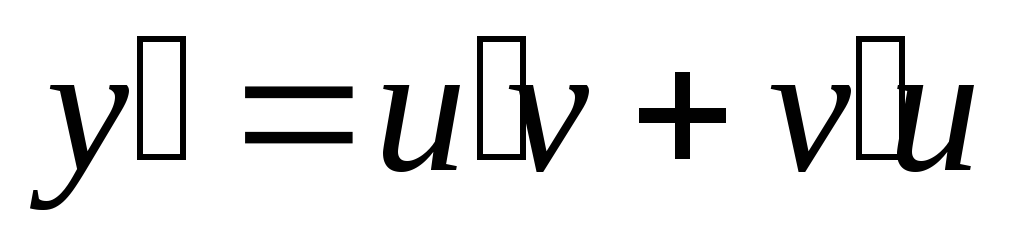 .
Подставляя
.
Подставляя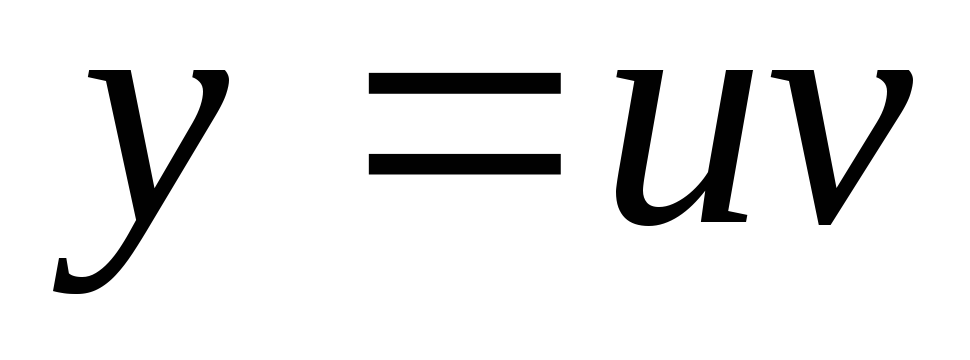 ,
,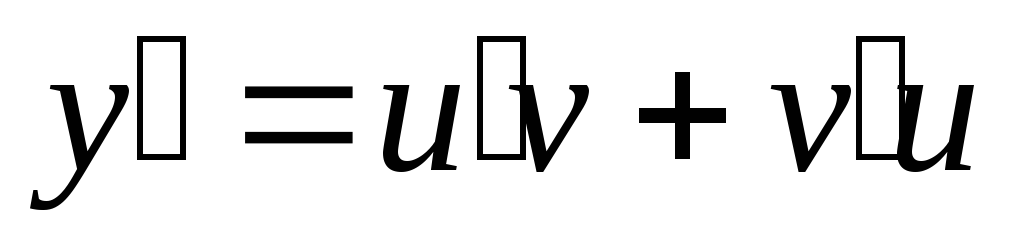 в
данное уравнение, получим
в
данное уравнение, получим
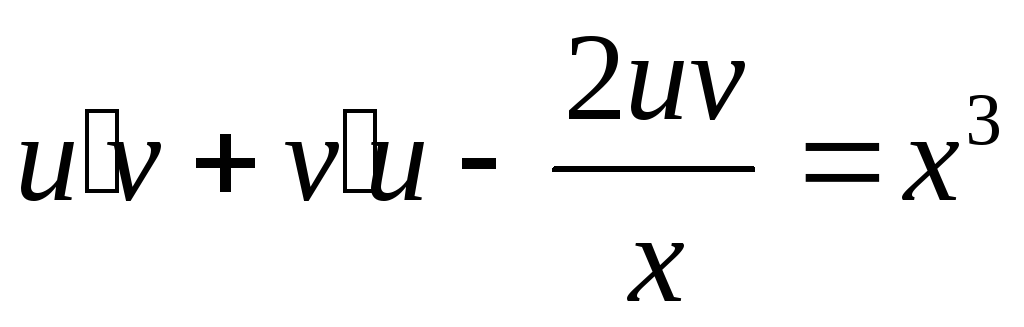
или
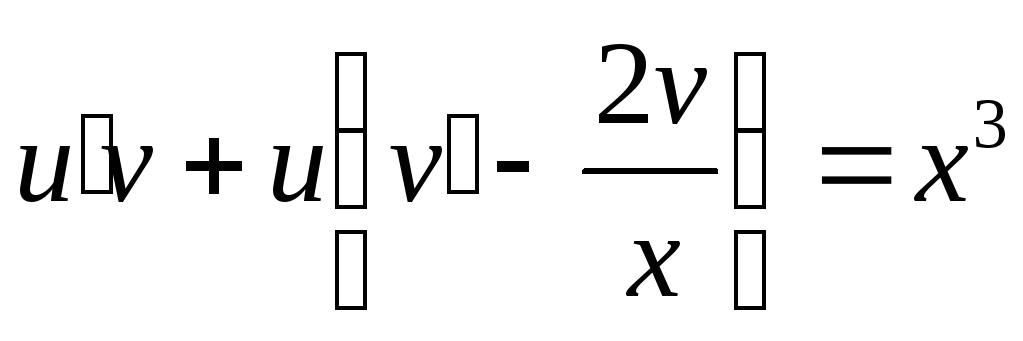 .
.
Приравняем нулю
выражение, стоящее в скобках и получим
уравнение с разделяющимися переменными
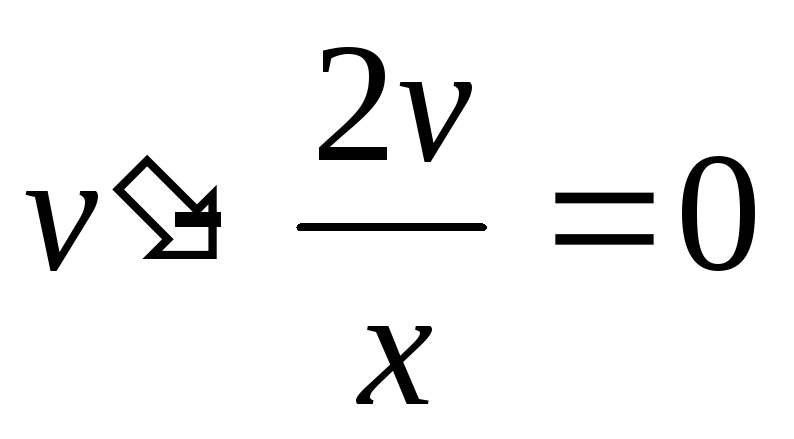 или
или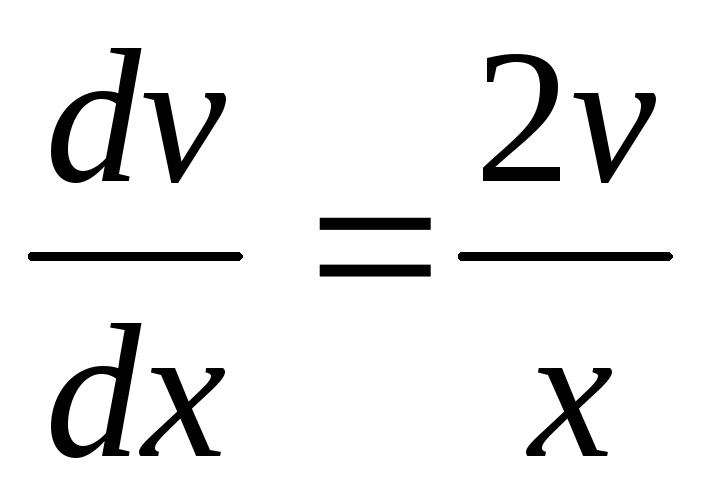 ,
или
,
или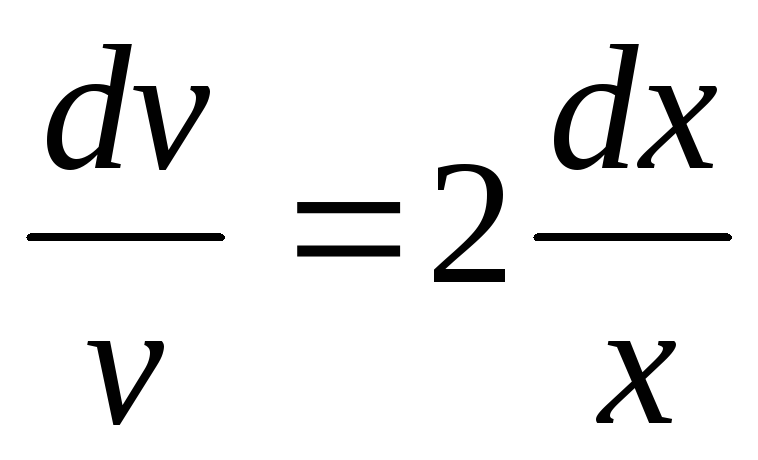 .
Интегрируя обе части уравнения, находим
.
Интегрируя обе части уравнения, находим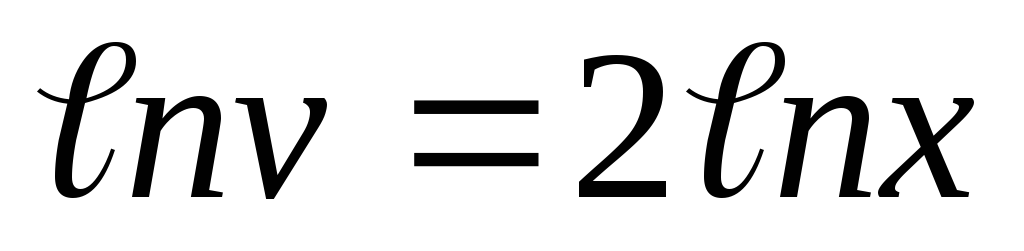 или
или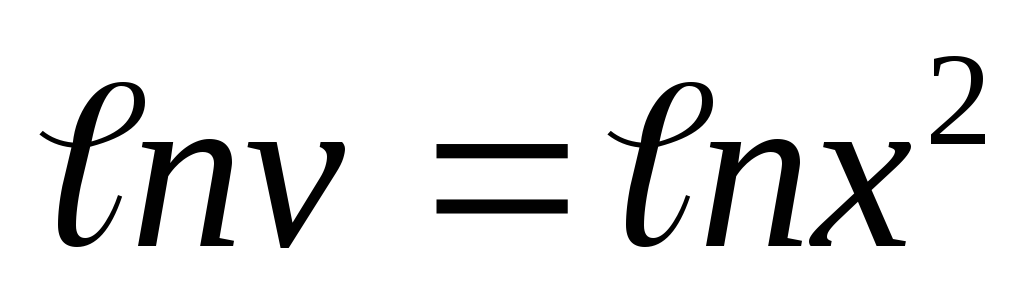 (Здесь
полагают произвольную постоянную равной
нулю). Откуда
(Здесь
полагают произвольную постоянную равной
нулю). Откуда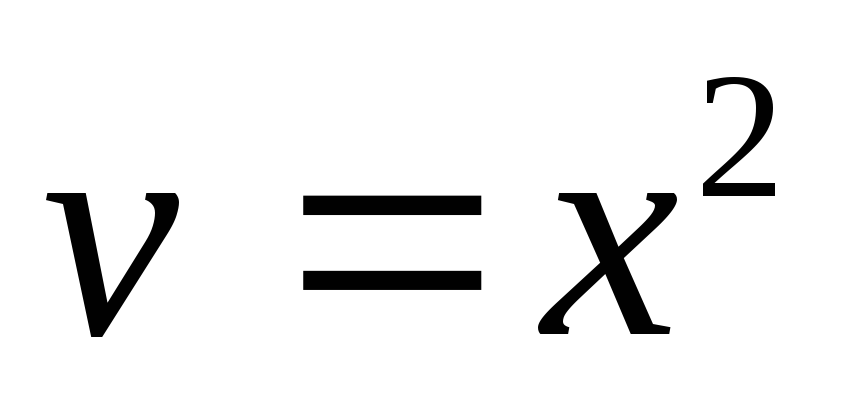 .
Подставляя его уравнение
.
Подставляя его уравнение ,
придем к его общему уравнению с
разделяющимися переменными
,
придем к его общему уравнению с
разделяющимися переменными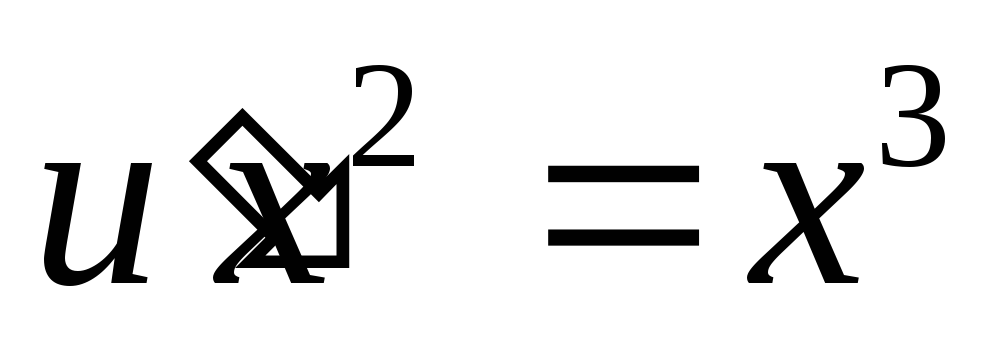 или
или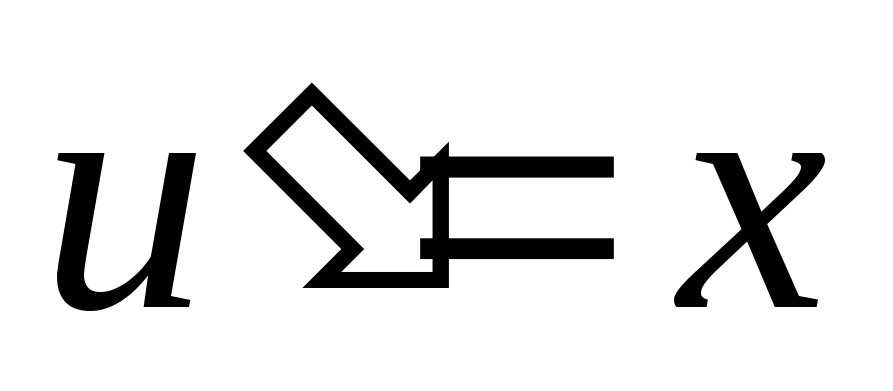 ,
или
,
или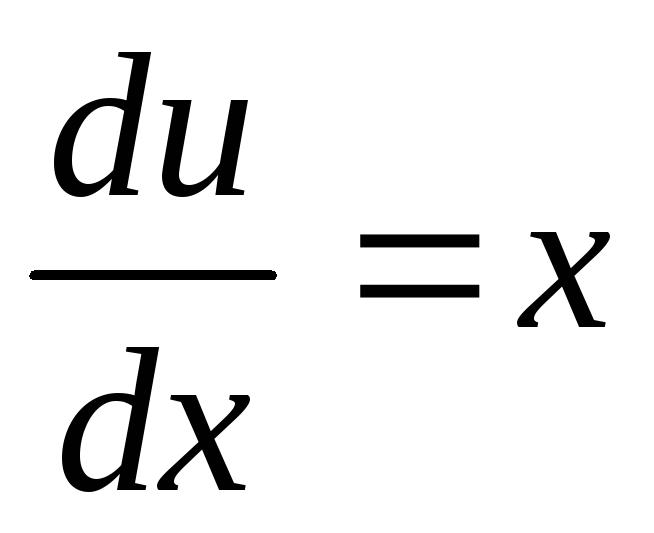 ,
или
,
или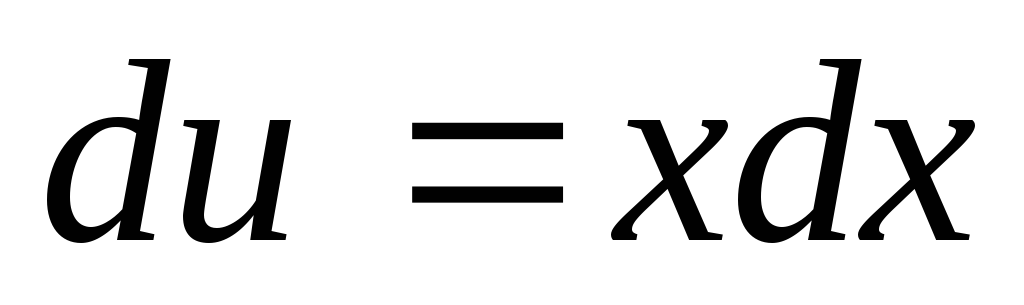 ,
откуда
,
откуда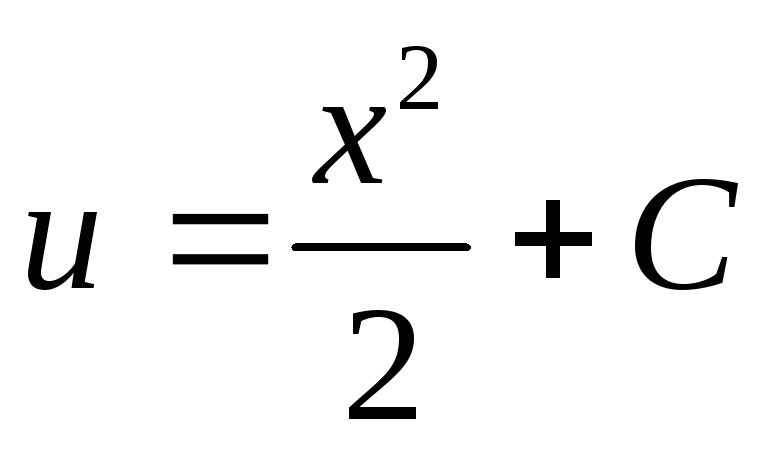 .
.
А так как решение
ищется в виде
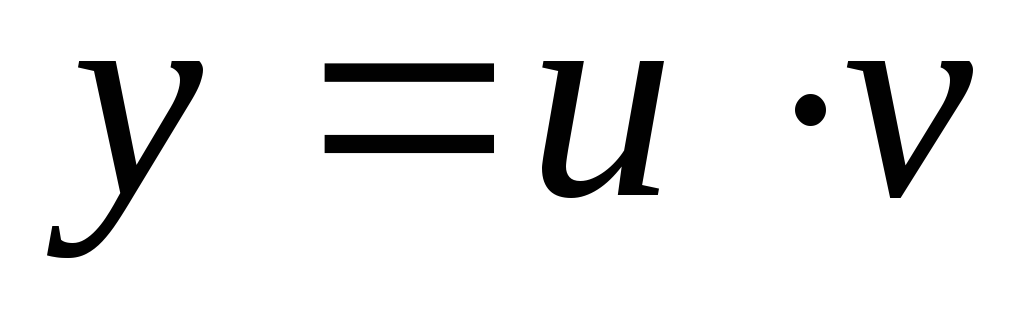 ,
то оно будет таким
,
то оно будет таким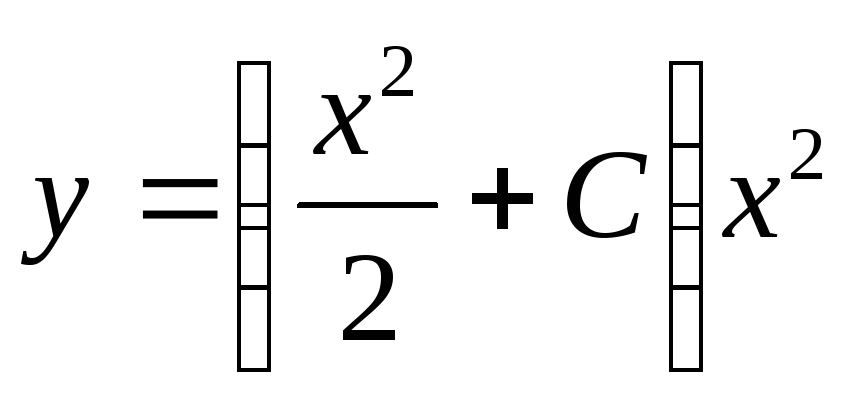 .
Это- общее решение, в котором
.
Это- общее решение, в котором -
произвольная постоянная. Решим теперь
задачу Коши: из общего решения по заданным
начальным условиям определим частное
решение. Для этого подставим в общее
решение начальные условия. Получим
-
произвольная постоянная. Решим теперь
задачу Коши: из общего решения по заданным
начальным условиям определим частное
решение. Для этого подставим в общее
решение начальные условия. Получим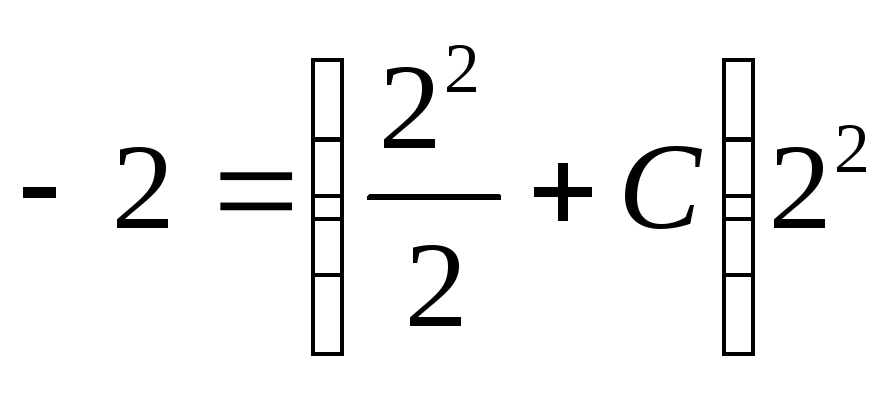 или
или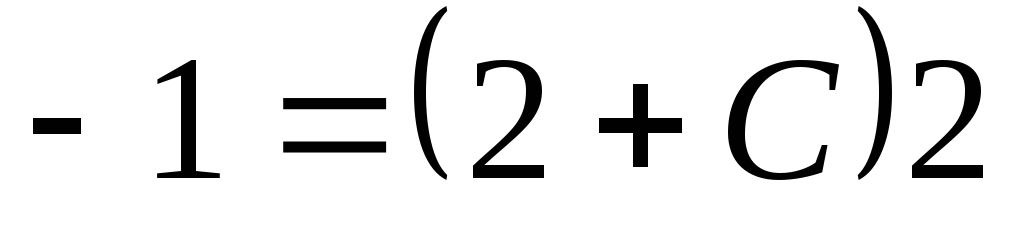 ,
или
,
или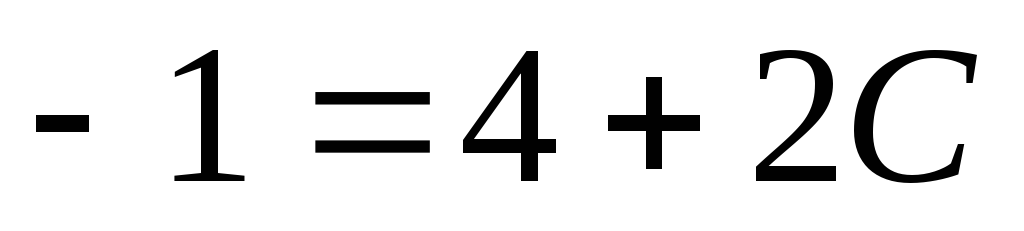 ,
или
,
или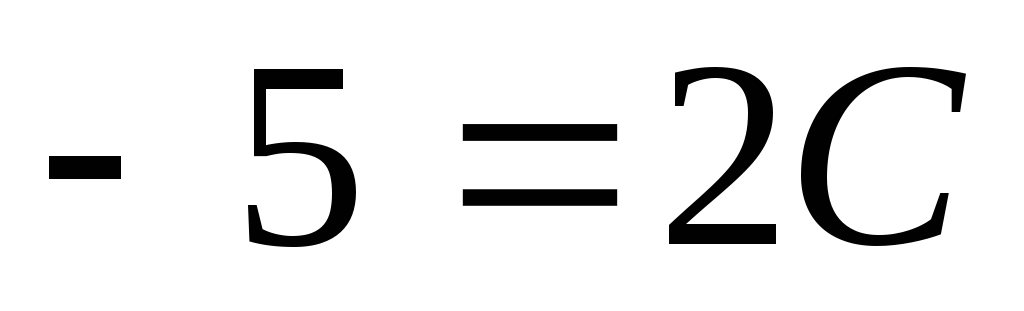 ,
откуда
,
откуда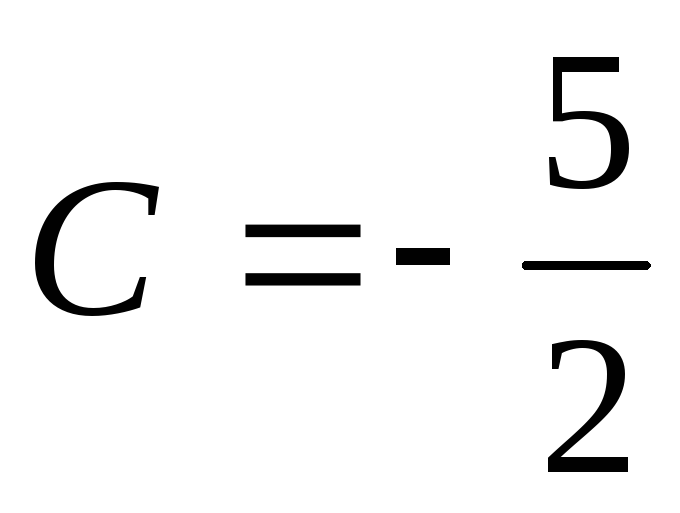 .
Подставляя это значение постоянной в
общее решение, получим частное решение
.
Подставляя это значение постоянной в
общее решение, получим частное решение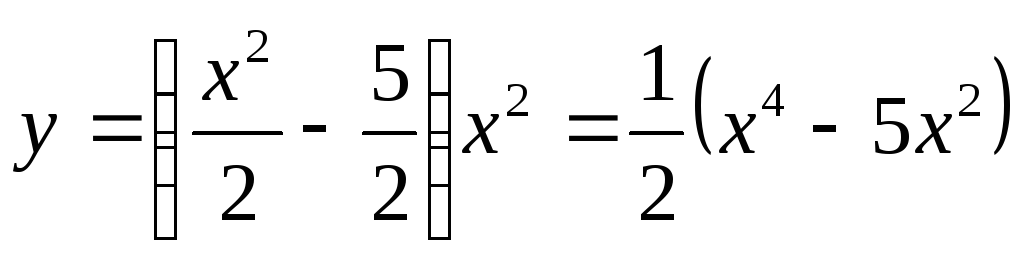 удовлетворяющее начальным условиям.
удовлетворяющее начальным условиям.
Задача 15. Найти
область сходимости степенного ряда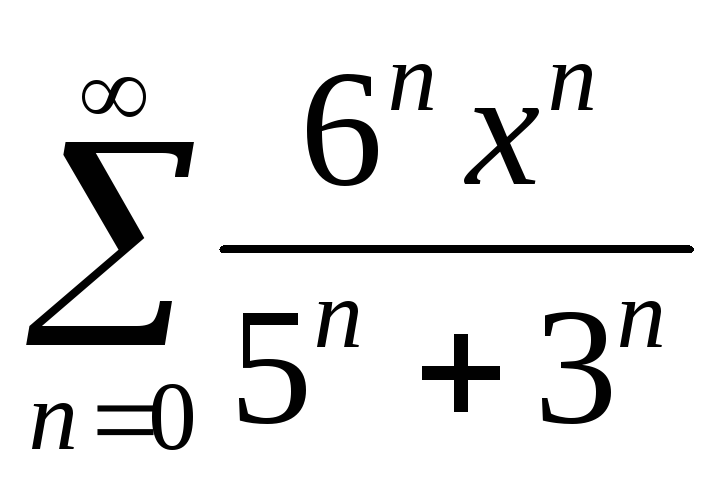 .
.
Решение.
Область сходимости
называется множество всех точек
сходимости данного ряда. Найдем радиус
и интервал сходимости.
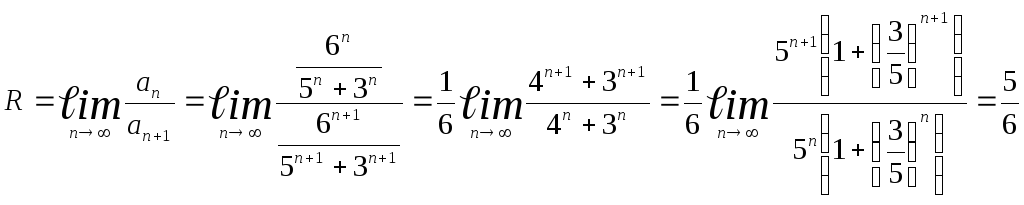 .
.
Где
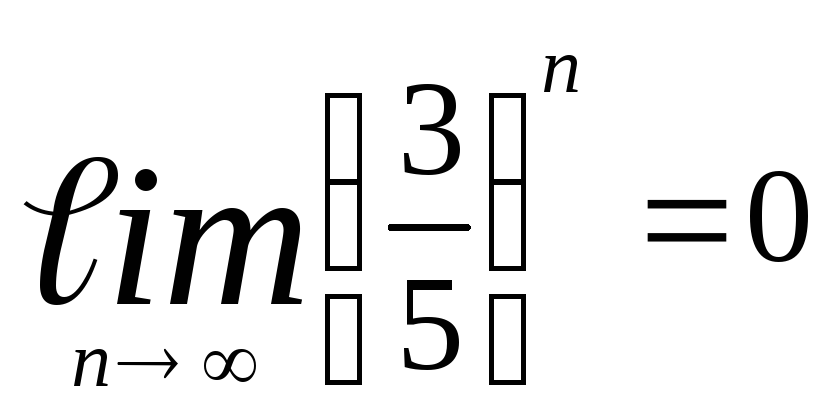 .
Радиус сходимости
.
Радиус сходимости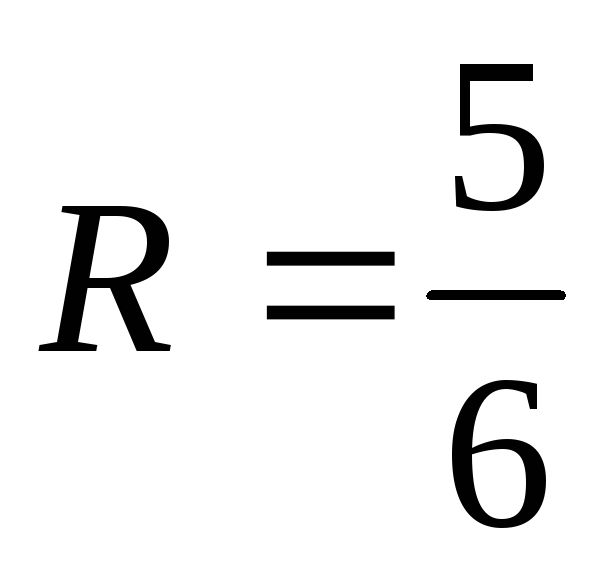 .
Тогда интервал сходимости
.
Тогда интервал сходимости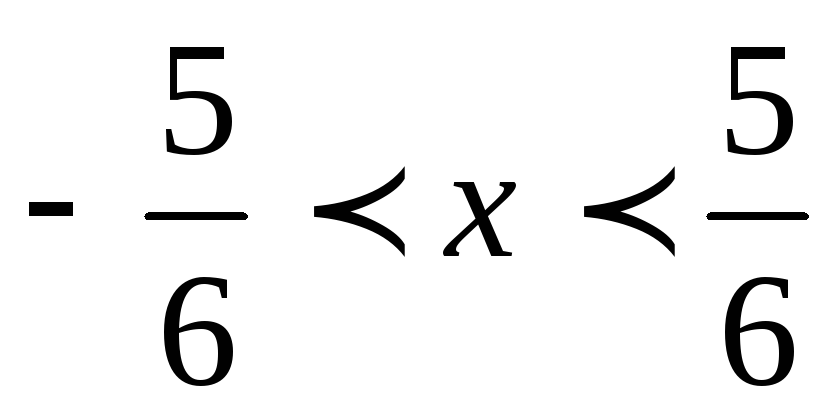 .
Исследуем сходимость ряда на концах
этого интервала.
.
Исследуем сходимость ряда на концах
этого интервала.
Подставим в данный
степенной ряд
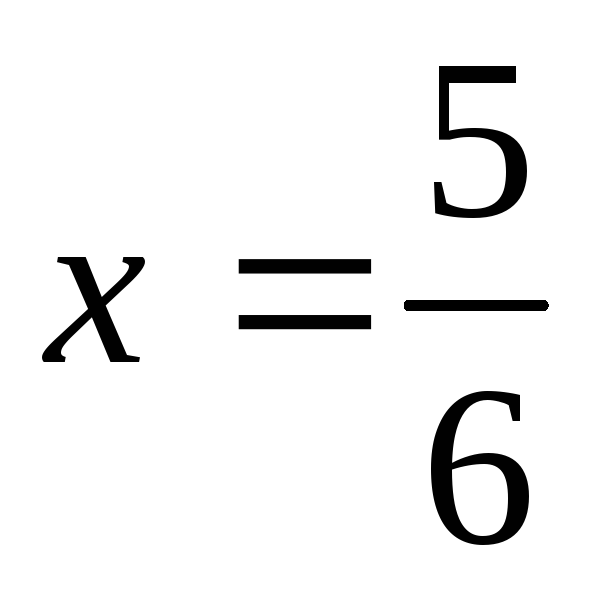 .
Получим числовой ряд
.
Получим числовой ряд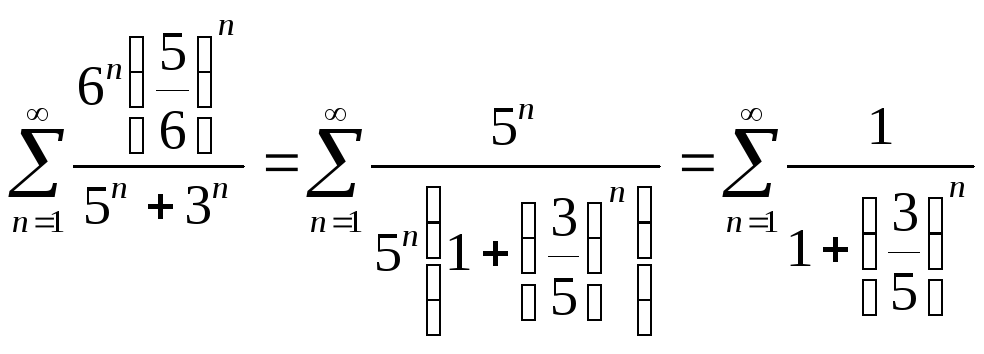 .
Этот ряд является расходящимся, так
как не выполняется необходимое условие
его сходимости
.
Этот ряд является расходящимся, так
как не выполняется необходимое условие
его сходимости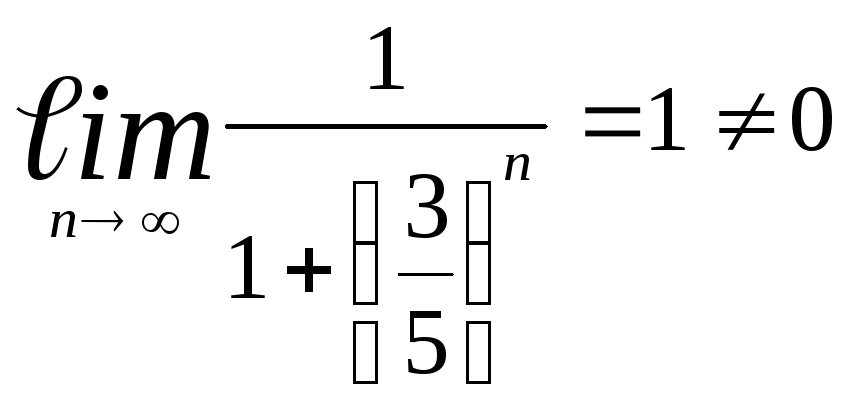 .
.
Подставляя в
степенной ряд
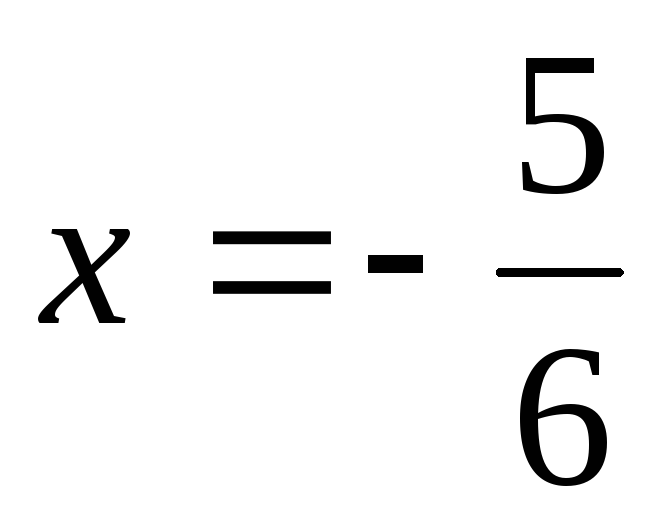 ,
получим знакочередующийся числовой
ряд
,
получим знакочередующийся числовой
ряд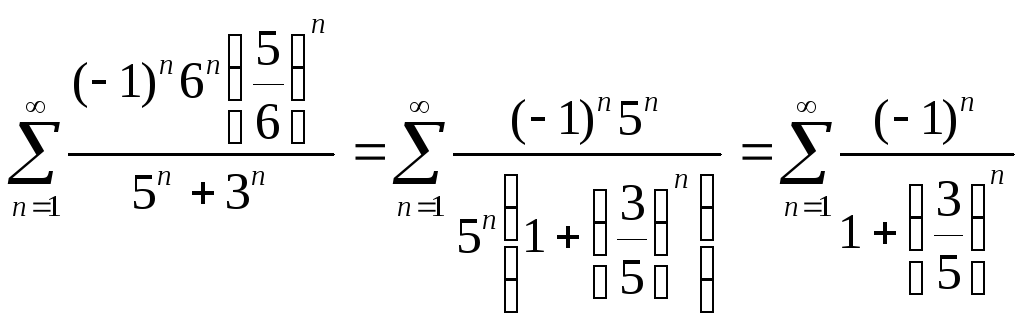 ,
который расходится по той же причине:
его общий член при
,
который расходится по той же причине:
его общий член при стремится к 1, а не к 0.
стремится к 1, а не к 0.
Итак, область
сходимости данного степенного ряда
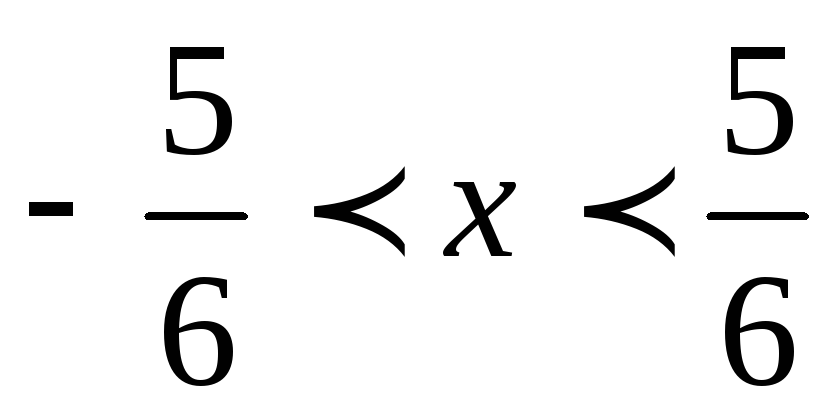 .
.


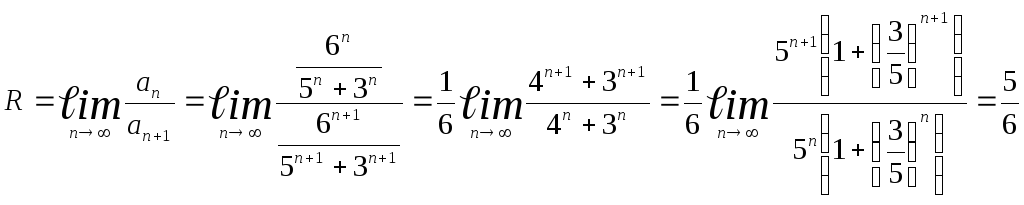 .
.
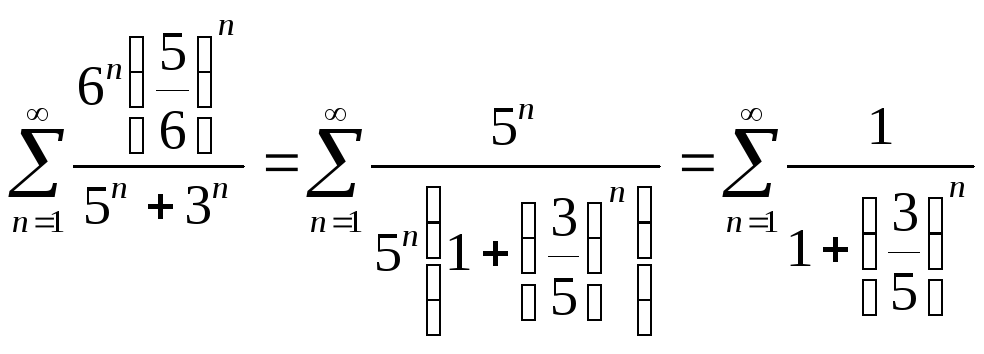 .
Этот ряд является расходящимся, так
как не выполняется необходимое условие
его сходимости
.
Этот ряд является расходящимся, так
как не выполняется необходимое условие
его сходимости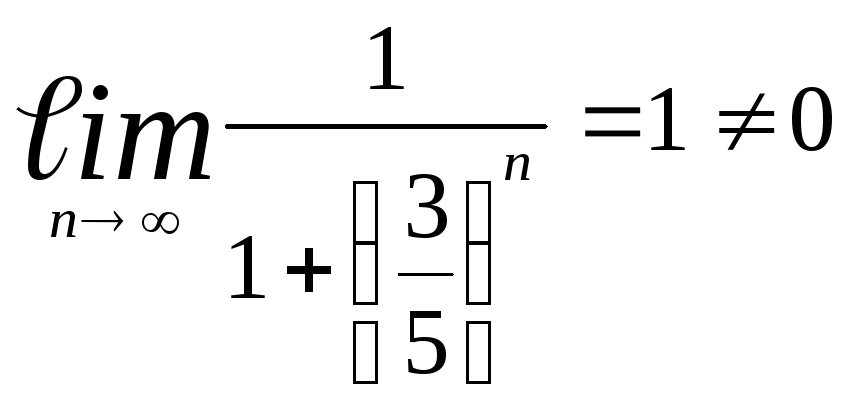 .
.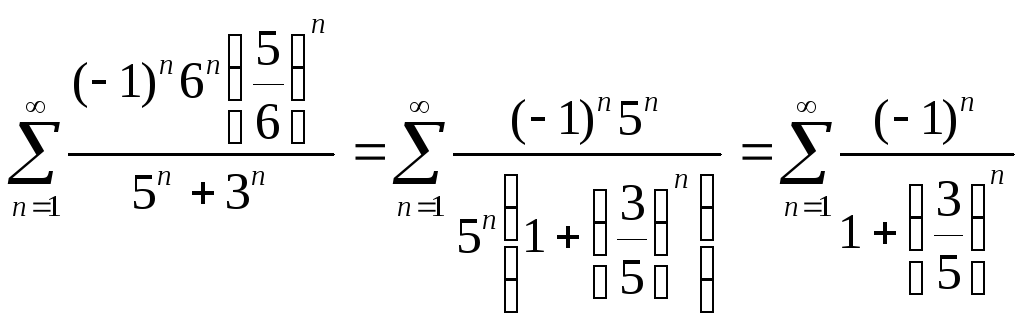 ,
который расходится по той же причине:
его общий член при
,
который расходится по той же причине:
его общий член при