ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ

Кафедра ТОЭ

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

(часть 3)

Расчет электрического поля трехпроводной линии

Методическое указание к выполнению контрольной работы № 1

Составитель Шаталов А.Ф.

Ставрополь 2013г

Цель работы

Рассчитать потенциал и напряженность электрического поля вблизи трехпроводной линии в заданной точке, энергию поля на единицу длины линии.

Условие и варианты работы

Трехпроводная линия (радиус проводов R=0.02 м), расположена в воздухе () параллельно проводящей плоскости (земли), как показано на рис.1. Координаты проводов и их потенциалы заданы в табл.1.

Требуется:

1. Определить потенциальные и емкостные коэффициенты, частичные емкости, линейные плотности зарядов проводов, энергию электростатического поля на единицу длины,

а также для точки N (координаты x, y) рассчитать потенциал  и вектор напряженности .

Таблица 1

№ вар	Потенциалы проводов				Координаты проводов							Коорди-наты т.N
											Х		y
	кВ	кВ	кВ	м		м	м	м	м	м	м		м
1	1	-10	9	2		4	6	5	5	5	4		7
2	7	2	-9	5		5	5	5	7	9	7		7
3	5	-8	3	4		4	7	5	7	5	7		7
4	-7	4	3	3		5	5	5	5	7	3		7
5	5	-6	1	3		6	9	5	7	5	6		5
6	-1	6	-5	3		6	9	7	5	7	6		7
7	-3	-4	7	3		5	7	4	4	4	5		2
8	-3	8	-5	4		4	4	4	6	8	2		6
9	9	-2	-7	3		3	7	4	6	4	7		2
10	-9	10	-1	3		6	6	4	4	7	6		2
11	-8	-2	10	3		5	7	4	7	4	3		7
12	-3	9	-6	3		5	7	7	4	7	7		4
13	8	-4	-4	2		5	8	4	6	8	5		4
14	-2	7	-5	2		4	6	7	5	3	4		7
15	-2	-6	8	3		4	7	5	6	5	5		5
16	-7	5	2	3		4	7	5	4	5	4		5
17	4	-8	4	3		6	7	5	6	5	5		6
18	6	3	-9	3		6	7	5	4	5	5		4
19	8	-10	2	3		4	6	5	5	3	4		3
20	-9	1	8	3		4	6	3	3	5	6		3
21	10	-8	-2	2		5	6	6	4	4	6		6
22	3	-9	6	2		5	6	3	5	5	3		5
23	-5	-3	8	3		4	6	5	5	5	5		5
24	2	-7	5	3		5	6	4	4	4	4		4
25	-6	3	3	5		5	5	3	4	7	5		5
26	5	4	-3	3		3	5	3	8	1	3		4
27	-1	2	0	2		2	3	2	4	1	2		3
28	0	10	-10	1		2	3	4	4	2	1		1
29	1	1	-2	2		1	4	1	2	1	2		3

Методические указания к выполнению работы

Для трехпроводной линии, расположенной в воздухе параллельно поверхности земли справедливы группы формул Максвелла.

Первая группа формул:

,

(1)

где 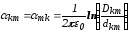- собственные и взаимные потенциальные коэффициенты (м/Ф) соответственно, причем km;

- расстояние между k и m проводами (м);

- расстояния между k проводом и зеркальным изображением m провода (м);

и - координаты проводов; R – радиус проводов (м);

- потенциалы проводов (В) ; ;

- линейные плотности зарядов проводов .

По заданным координатам проводов и известном R=0.02 м рассчитываются собственные 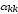и взаимные потенциальные коэффициенты проводов линии.

Вторая группа формул:

,

(2)

где

- собственные (k=m) и взаимные (km) емкостные коэффициенты ;

-определитель системы уравнений (1);

- минор, образованный вычеркиванием k строки и m столбца определителя , например:

=.

По предварительно полученным потенциальным коэффициентам рассчитываются собственные и взаимные емкостные коэффициенты.

Затем по формулам (2) находятся линейные плотности зарядов проводов .

Третья группа формул:

,

(3)

где

- собственные частичные емкости (Ф/м);

- взаимные частичные емкости при km .

По предварительно найденным емкостным коэффициентам определяются частичные емкости. Далее необходимо сделать проверку правильности расчета линейных плотностей зарядов проводов и их коэффициентов. Для этого в систему (1) подставляются найденные величины () и определяются потенциалы проводов , которые сравниваются с заданными значениями.

Энергию электростатического поля на единицу длины линии можно рассчитать по формуле:

Для точки N с заданными координатами x,y потенциал  и вектор напряженности определяются методом наложения с учетом зеркальных изображений проводов линии:

; ,

где

- составляющая потенциала, создаваемая зарядом k провода и его зеркальным изображением (В);

- расстояние от точки N до k провода (м);

- расстояние от точки N до зеркального изображения k провода (м);

модуль вектора напряженности , создаваемый зарядом k провода;

модуль вектора напряженности , создаваемый зеркальным изображением заряда k провода.

Потенциал  равен алгебраической сумме составляющих потенциала , причем числовые значения подставляются со своими знаками. Вектор напряженности необходимо определить графическим сложением векторов и от всех зарядов и их зеркальных изображений, которые направлены вдоль радиусов и соответственно, причем при вектор направлен от k провода и вектор направлен к зеркальному изображению провода, а при направления векторов и меняются на противоположные.
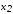