
1.пределы, производная
..docМатематический анализ.


§1. Функция. Предел функции
Определение
1. Функция,
заданная уравнением
![]() ,
называется
явной.
,
называется
явной.
Пример: у=2х, у=sinx - явные функции,
У явно выражен через Х
Определение
2. Функция,
заданная уравнением
![]() ,
называется неявной
,
называется неявной
Например,
 - неявная функция от х.
- неявная функция от х.
У явно не выражен через Х
Определение
3 (по
Гейне).
Число
b
называется пределом функции
![]() при
при
![]() ,
если для любой последовательности
значений аргумента х, сходящейся к а,
соответствующая последовательность
значений функций сходится к числу b.
,
если для любой последовательности
значений аргумента х, сходящейся к а,
соответствующая последовательность
значений функций сходится к числу b.
Обозначение:
b = lim f(x)
 x a
x a
Если
![]() ,
то х
может оставаться меньше а
или больше а.
,
то х
может оставаться меньше а
или больше а.
В связи с этим существуют так называемые односторонние пределы:


Пример.


Если функция в данной точке непрерывна, то односторонние пределы равны.
§2. Теоремы о пределах
-
Предел постоянной:

-
Предел алгебраической суммы функций.

-
Предел произведения функций:

Следствие: постоянный множитель можно выносить за знак предела:

-
Предел частного функций:
 где
где

-
Предел степени :

§3. Бесконечно малые и бесконечно большие функции
Определение
1.
Функция
![]() - бесконечно
большая
при значении
- бесконечно
большая
при значении
![]() ,
если
,
если
![]() .
.
Определение
2.
Функция
![]() - бесконечно малая при значении
- бесконечно малая при значении
![]() ,
если
,
если
![]() .
.
Свойства б. м. ф. и б. б. ф.
1. Сумма, разность, произведение б.м.ф., а также произведение б.м.ф. на постоянную величину – б.м.ф.
 - является
неопределенностью вида
- является
неопределенностью вида
![]()
2.
![]() ,
,
 ,
,
 -
б.б.ф.
-
б.б.ф.
![]() ,
,
![]() - являются
неопределенностями.
- являются
неопределенностями.
3.
Если
![]() - б. б. ф. при значении
- б. б. ф. при значении
![]() ,
то
,
то
![]() - б. м. ф. при значении
- б. м. ф. при значении
 ,
где
,
где
![]() ,
,
![]() .
.
4. Если
![]() - б. м. ф. при значении
- б. м. ф. при значении
![]() ,
то
,
то
![]() - б. б. ф. при значении
- б. б. ф. при значении
![]() ,
где
,
где
![]() ,
,
![]() .
.
5. Соотношения
вида
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() тоже являются неопределённостями.
тоже являются неопределённостями.
§4. Раскрытие
неопределенности вида
 при
вычислении пределов.
при
вычислении пределов.
Непосредственное вычисление пределов.
Вместо аргумента х подставляют его предельное значение в функцию.
Пример:

Правило
раскрытия неопределенности вида

Если дробь содержит многочлены, то их следует разложить на линейные множители и выполнить сокращение.
Пример:

Если под знаком предела есть иррациональные выражения, то нужно умножить числитель и знаменатель на сопряженные множители к этим выражениям.
§5.
Раскрытие неопределенности вида при
вычислении пределов.
при
вычислении пределов.
Состоит в почленном делении числителя и знаменателя на переменную в наивысшей степени.
Пример:

Замечание:
-
Если старшие степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях переменной.
-
Если степень числителя меньше степени знаменателя, то предел равен нулю.
-
Если степень числителя больше степени знаменателя, то предел равен бесконечности.
§6. Два замечательных предела

-
Первый замечательный предел.
 или
или

Он
раскрывает неопределенность вида
![]() .
.
Пример:
 .
.
-
Второй замечательный предел.
 или
или

Он раскрывает
неопределенность вида
 (е ≈ 2, 718281828459045…..).-
неперово число.
(е ≈ 2, 718281828459045…..).-
неперово число.
(е ≈ 2, 72).

Пример:

§7. Непрерывность функции. Точки разрыва.
Определение
1. Функция
![]() называется непрерывной
в некоторой точке
называется непрерывной
в некоторой точке
![]() ,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции, т.е.
,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции, т.е.

Определение
2. Функция
![]() ,
непрерывная в каждой точке некоторого
интервала
,
непрерывная в каждой точке некоторого
интервала
![]() ,
называется непрерывной
на всем интервале.
,
называется непрерывной
на всем интервале.
Определение 3. Точка, в которой нарушается непрерывность функции, называется точкой разрыва.
Существуют точки разрыва 1-го и 2-го рода.
-
Если односторонние пределы функции в данной точке не равны и конечные, то такая точка называется точкой разрыва 1-го рода.
Скачок функции в этой точке равен модулю разности односторонних пределов:

Пример:


![]() – точка разрыва
1-го рода. Можно указать скачок функции:
– точка разрыва
1-го рода. Можно указать скачок функции:

-
Если в данной точке хотя бы один из односторонних пределов бесконечен или не существует, то такая точка называется точкой разрыва 2-го рода.
§8. Свойства функций, непрерывных на отрезке
1 )
)
Функция
![]() ,
непрерывная на отрезке
,
непрерывная на отрезке
![]() ,
достигает на этом отрезке своего
наибольшего и наименьшего значения.
,
достигает на этом отрезке своего
наибольшего и наименьшего значения.

Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и принимает на концах этого отрезка
значения разных знаков, то на этом
отрезке существует, по крайней мере,
одно такое значение
и принимает на концах этого отрезка
значения разных знаков, то на этом
отрезке существует, по крайней мере,
одно такое значение
![]() ,
что
,
что
![]() .
.
3)
Если две функции
![]() и
и
![]() непрерывны на отрезке
непрерывны на отрезке
 ,
то непрерывны
,
то непрерывны
![]() ,
,
 ,
,
 на этом отрезке.
на этом отрезке.
§9. Производная функции. Дифференцируемость функций


Определение
1. Производной
функции
![]() называется предел (если он существует)
отношения приращения функции к приращению
аргумента при стремлении приращения
аргумента к нулю:
называется предел (если он существует)
отношения приращения функции к приращению
аргумента при стремлении приращения
аргумента к нулю:

Обозначения:

Определение
2. Функция
![]() ,
имеющая в точке
,
имеющая в точке
![]() производную, называется дифференцируемой
в этой точке.
производную, называется дифференцируемой
в этой точке.
Определение
3. Функция
![]() ,
дифференцируемая в каждой точке интервала
,
дифференцируемая в каждой точке интервала
![]() ,
дифференцируема на этом интервале.
,
дифференцируема на этом интервале.
Связь непрерывности и дифференцируемости функции.
Теорема.
Если
функция
![]() дифференцируема в некоторой точке
дифференцируема в некоторой точке
![]() ,
то в этой точке она и непрерывна. Обратное
утверждение неверно, т.к. есть функции
непрерывные в точке, но не имеющие
производной в этой точке.
,
то в этой точке она и непрерывна. Обратное
утверждение неверно, т.к. есть функции
непрерывные в точке, но не имеющие
производной в этой точке.
Пример:
Функция
![]() в точке
в точке
![]() непрерывна, но не имеет производной.
непрерывна, но не имеет производной.

Таблица основных производных
-
 15.
15.

-
 16.
16.
-
 17.
17.

-
 18.
18.

-
 19.
19.

-
 20.
20.

-
 21.
21.

-
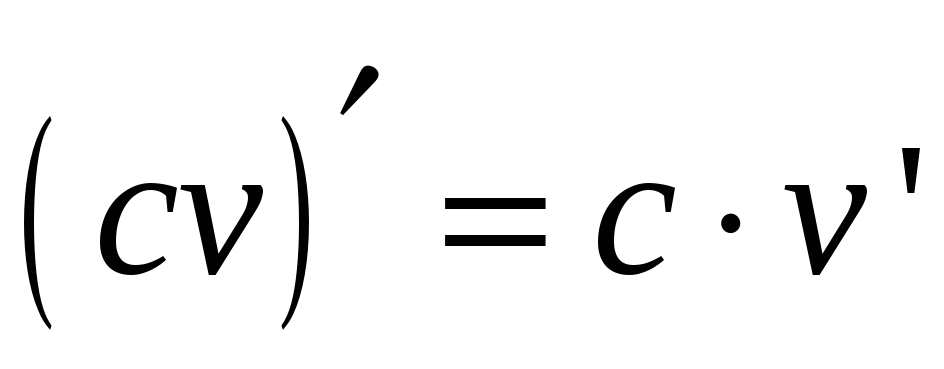 22.
22.

-
 23.
23.

-

-

-

-

-

§10. Производная сложной и обратной функции
1.
производная сложной функции
Если
![]() и
и
![]() ,
то
,
то
![]() - сложная функция от х,
где
- сложная функция от х,
где
u - промежуточный аргумент,
х - конечный аргумент.
Теорема. Производная сложной функции равна производной функции по промежуточному аргументу u умноженной на производную промежуточного аргумента по конечному аргументу х, т.е.
![]() или
или

Пример.
(sinU)′
= cosU
![]() U′
U′
(sin3х)′
= cos3х
![]() (3х)′
(3х)′
2. производная обратной функции

Пусть
![]() дифференцируемая и строго монотонная
функция на некотором промежутке х.
Тогда функция
дифференцируемая и строго монотонная
функция на некотором промежутке х.
Тогда функция
![]() - ей обратная функция.
- ей обратная функция.
Теорема. Производная обратной функции равна:
 .
.
§11. Производные высших порядков
Пусть
задана некоторая дифференцируемая
функция
![]() .
Тогда:
.
Тогда:
-
 - производная
1-го порядка.
- производная
1-го порядка.
Если
![]() - это опять функция от х,
то от нее можно найти производную:
- это опять функция от х,
то от нее можно найти производную:
-
 - производная
2-го порядка.
- производная
2-го порядка. -
 - производная
3-го порядка.
- производная
3-го порядка.
… …………. …………………………... .
n)
 - производная n-го
порядка.
- производная n-го
порядка.
Пример:


§12. Дифференцирование неявных функций
![]() - функция,
заданная неявно, т.е. функция не разрешена
относительно у.
- функция,
заданная неявно, т.е. функция не разрешена
относительно у.
Чтобы найти
производную неявной функции, следует
все члены выражения
![]() продифференцировать
по х,
а затем выразить у´
через х;
у и const,
помня, что
продифференцировать
по х,
а затем выразить у´
через х;
у и const,
помня, что
![]() ,
а
,
а
![]() .
.
Пример:


Аналогично можно
находить производную 2-го порядка
![]() .
Для этого выражение (1) нужно еще раз
продифференцировать по х
и выразить у´´
через х;
у; у´ и
const.
Затем в полученное выражение подставить
значение у´.
.
Для этого выражение (1) нужно еще раз
продифференцировать по х
и выразить у´´
через х;
у; у´ и
const.
Затем в полученное выражение подставить
значение у´.
§12А. Геометрический смысл производной
Значение производной функции в точке равно тангенсу угла наклона касательной, проведенной к графику функции в этой точке:


Уравнение касательной:
![]()
Уравнение нормали:
 ,
где (
,
где ( - точка
касания.
- точка
касания.
12б Производная – это мгновенная скорость изменения функции

§13. Понятие дифференциала

Пусть
дана функция
![]() .
По определению:
.
По определению:
 .
По теореме о пределах имеем: если
.
По теореме о пределах имеем: если
 ,
то
,
то
![]() - значит
- значит
 ,
получим:
,
получим:
![]() .
.
Определение
1. Главная
часть приращения
![]() ,
линейная относительно
,
линейная относительно
![]() ,
называется дифференциалом
функции
и обозначается dy:
,
называется дифференциалом
функции
и обозначается dy:
![]() .
.
 .
.
Рассмотрим
функцию
![]() .
.
![]() .
Следовательно, формула дифференциала
функции в конечном результате имеет
вид:
.
Следовательно, формула дифференциала
функции в конечном результате имеет
вид:
![]() .
.
Пример:

С
геометрической точки зрения дифференциал
функции
![]() равен
равен
приращению ординаты касательной.
§14. Применение дифференциала функции к приближенным вычислениям
Пусть
задана функция
![]() .
Воспользуемся приближенным равенством:
.
Воспользуемся приближенным равенством:
 .
.
Сравнивая (1) и (2) выражения, получим:
![]()
![]()
![]() - формула для
приближенного
вычисления
значений функции.
- формула для
приближенного
вычисления
значений функции.
Можно доказать,
что абсолютная погрешность этой формулы
не превышает величины
 .
.
Пример:
Вычислить
![]() .
.
Пусть
![]()


![]()


§15. Правило Лопиталя при вычислении пределов
Пусть
заданы некоторые функции
![]() и
и
![]() ,
дифференцируемые на некотором интервале
,
дифференцируемые на некотором интервале
![]() ,
а в точке
,
а в точке
![]() обращающиеся в ноль. Тогда имеет место
равенство:
обращающиеся в ноль. Тогда имеет место
равенство:
 -для
-для
раскрытия
неопределенностей
![]() и
и
![]() - правило
Лопиталя
- правило
Лопиталя
Пример1: Найти предел.

 ;
;
Пример2:
Найти предел
![]() .
.
![]() ;
;
![]() ;
;
![]() - опять получилась
неопределенность. Применим правило
Лопиталя еще раз.
- опять получилась
неопределенность. Применим правило
Лопиталя еще раз.
![]() ;
;
![]() ;
;
![]() - применяем правило
Лопиталя еще раз.
- применяем правило
Лопиталя еще раз.
![]() ;
;
![]() ;
;
