статистика формулы

Мода (Мо) – это наиболее часто встречающиеся значение признака в виду распределения. Если ряд интервальный, то мода рассчитывается по формуле:

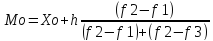
Xo – нижняя граница модального интервала. Модальным интервалом называют интервал, для которого частота максимальна.

n – Величина модального интервала

f1 – частота интервала предшествующего периода

f2 - частота модального интервала

f 3 – частота интервала последующего после модального.

Медиана (Ме) – это значение признака, по которому совокупность делится пополам, т.е. серединное значение признака в ряду распределений. Медиана находится по формуле:

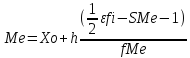
Xo – нижняя граница медианного интервала.

Медианном является интервал, в котором сумма накопленных частот первой превышает половину всех частот (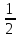S).

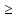
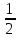
SMe fi

h – Величина медианного интервала

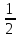
fi - полусумма всех частот.

S Me-1 – сумма накопленных частот предшествующего медианному

f Me – частота медианного интервала.

Квартили:

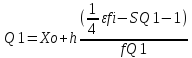
Децели:

Для оценки дифференциации единиц совокупности по варьирующему признаку рассчитывается децельный коэффициент дифференциации (ДКД)

ДКД =

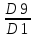
I. Расчет показателей размера и интенсивности вариации. Для оценки размера вариации рассчитываются абсолютные вариации:

- размах вариации характеризует разность между наибольшим и наименьшим значением признаков.

1) R = Xmax - Xmin

2) среднее линейное отклонение

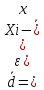простая.

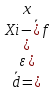взвешенная

3) 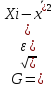простая.

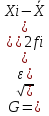взвешенная

Дисперсия

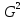
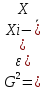простая 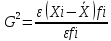взвешенная

, где простая.

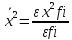
1. Коэффициент асилляции Ко

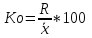
Характеризует относительную колеблемость крайних значений признаков вокруг средней величины

2. 

Характеризует долю усредненного значения абсолютных отклонений индивидуальных значений признака от его средней величины.

3. Коэффициент вариации V

По коэффициенту вариации судят о характере вариации признака, о составе совокупности единиц.

Оценка вариационного ряда на асимметрию и эксцесс. Для оценки степени асимметрического ряда применяется коэффициент асимметрии As.

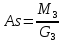
M3 – центральный момент третьего порядка.

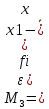
Также необходимо оценить степень существенности асимметрии распределения с помощью средней квадратической ошибки коэффициент асимметрии.

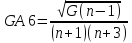, n – количество групп

Под экцессом понимают островершинность или плосковершинность распределения по сравнению с нормальным при той же силе вариации.

;

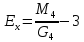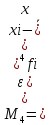
Существенность экцесса распределения определяют через среднеквадратическую ошибку.