
Информатика / KompleksKurs
.pdf
От математики к информатике
:Используя стандартные текстовые редакторы или редактор Word из пакета Microsoft Office напечатать несколько высказываний. Составить из них новые (составные) высказывания и определить их истинность.
:Составить таблицы истинности для формул, указанных в заданиях 2.1., 2.2. и 2.3., при помощи электронных таблиц Excel из пакета Microsoft Office.
Теория вероятностей с элементами комбинаторики
Теория
Задачи, в которых речь идет о тех или иных комбинациях (выборах) называют комбинаторными. Решение большинства комбинаторных задач основано на двух простых правилах - суммы и произведения.
Правило суммы. Если элемент a может быть выбран n способами, а элемент b - m способами, причем выборы несовместны, то выбор «либо a, либо b» может быть сделан (m+n) способами. Например, элемент множества А={а; b; с; d} можно выбрать 4 способами, элемент множества В={e; f; g} – 3 способами, а элемент множества АÈ В={а; b; с; d; e; f; g} 4+3=7 способами.
Правило включений и исключений.. Пусть даны два множества А и В, n(A) – число элементов множества А, n(В) – число элементов множества В, тогда: n(AÈB) = n(A) + n(B) - n(AÇB).
Для трех множеств: n(AÈBÈС) = n(A) + n(B) + n(С) - n(AÇB) - n(AÇС) - n(ВÇС) + n(АÇВÇС).
Пример. Из 40 студентов группы 35 человек успешно сдали экзамен по математике, а 37 – по русскому языку. Двое студентов получили неудовлетворительные отметки по обоим предметам. Сколько студентов имеют академическую задолженность? Решение: Пусть А – множество студентов не сдавших математику, n(А)=5, В – множество студентов не сдавших русский язык, n(В)=3. Известно, что n(АÇВ)=2. Найдем n(AÈB) = n(A) + n(B) - n(AÇB) = 5+3-2=6.
Правило произведения. Если элемент a можно выбрать m способами, а элемент b - n способами, то пару элементов (а; b) можно выбрать m·n способами.
Пример. Из деревни A в деревню B ведут три дороги, а из B в С ведут две дороги. Сколькими способами можно пройти из A в C через B? Решение: Дорогу из А в В можно выбрать 3-мя способами, а дорогу из В в С - 2-мя способами. Таким образом, пару дорог А-В и В-С можно выбрать 2*3=6 способами.
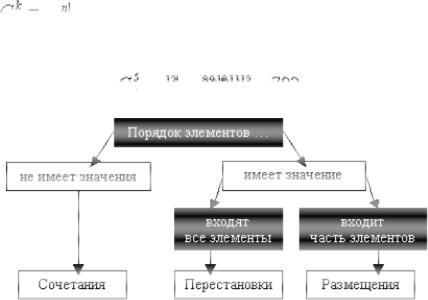
Пусть множество А содержит n различных элементов и пусть дано число k £ n. Тогда размещением без повторений называется любой упорядоченный набор, содержащий k элементов из данных n (два размещения считаются различными, если они отличаются порядком элементов или хотя бы одним элементом). Число всех размещений из n по k
обозначается: 
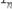

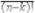 (n! = 1× 2× 3× …× n; говорят «n- факториал»).
(n! = 1× 2× 3× …× n; говорят «n- факториал»).
Пример. Сколько всего 6-ти значных телефонных номеров, в каждом из которых цифры
не повторяются? Решение. 





 = 5×6×7×8×9×10=151200.
= 5×6×7×8×9×10=151200.
Перестановкой без повторений из n элементов называется размещение без повторений из n элементов по n. Число всех перестановок из n элементов обозначается: Pn = n! Пример. Сколькими способами можно посадить на скамейку 9 человек? Решение. P9 = 9! =362880.
Сочетанием без повторений из n элементов по k называется любой неупорядоченный набор, содержащий k элементов из данных n. Число всех сочетаний из n по k
обозначается: 




 .
.
Пример. Сколькими способами можно выбрать делегацию в 5 человек из группы, содержащей 12 человек? Решение. Поскольку порядок членов делегации роли не играет,
применим формулу сочетаний. 











Для решения практических задач удобно использовать следующую схему:
***
Случайное событие – событие, которое в одном случайном эксперименте может произойти, а может и не произойти (обозначаются: А, В, С, D, … ).
Событие называется достоверным, если в результате эксперимента оно обязательно произойдет (обозначается: Ω). Событие называется невозможным, если в результате эксперимента оно не может произойти (обозначается: ). Событие A называется противоположным событию А, если в результате эксперимента обязательно происходит или событие А, или событие A, но одновременно оба эти события произойти не могут. События А и В – не совместны, если в одном и том же эксперименте они не могут произойти одновременно.
Например: Эксперимент (испытание) – бросание игральной кости. А – выпадение 1 или 2, или 3, или 4, или 5, или 6 очков (А=Ω), В – выпадение 1 и 2 очков (В= ),
Элементы математической статистики
Теория
Пусть в одинаковых условиях проводится n опытов и пусть в результате этих опытов мы получили х1, х2, …, хn данных (в общем случае – случайных величин). Так как проводится один опыт, то эти случайные величины можно считать конкретной реализацией какой-то одной случайной величины Х, которая называется генеральной совокупностью. х1, х2, …, хn – выборка из генеральной совокупности, число данных n – объем выборки, R =
xmax – xmin – размах выборки.
Пример. Путем опроса получены следующие данные о возрасте 25 студентов первого курса: 18, 17, 23, 18, 17, 19, 18, 20, 17, 22, 19, 21, 18, 18, 17, 22, 18, 21, 17, 21, 18, 19, 17, 23, 17. Объем выборки n = 25, размах выборки R = 25 – 17 = 6.
Как видно из примера, выборочные значения, записанные в порядке их регистрации обычно неудобны для дальнейшего анализа, поэтому проводят первичную обработку выборки:
1) Упорядочение.
Чаще всего выборку упорядочивают по возрастанию - х1£ х2£ …£хn. Такая упорядоченная выборка называется вариационным рядом. Например, показанная ранее выборка студентов будет иметь следующий вариационный ряд: 17, 17, 17, 17, 17, 17, 17,
18, 18, 18, 18, 18, 18, 18, 19, 19, 19, 20, 21, 21, 21, 22, 22, 23, 23.
2) Частотный анализ.
Пусть выборка х1, х2, …, хn содержит k(k£n) различных чисел: y1, y2, …, yk, причем число yi встречается ni раз. Число ni называется частотой элемента выборки yi. Ясно, что n1+ n2+…+ nk=n. Совокупность пар (yi; ni) называется статистическим рядом (или рядом распределения частот) выборки. Статистический ряд удобнее всего представлять в виде таблицы, в первой строке которой указываются значения, а во второй – их частоты. Например, для показанной нами выборки из 25 студентов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ni |
|
7 |
|
7 |
|
3 |
|
1 |
|
3 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина vi = ni/n называется относительной частотой значения yi. Ясно, что v1+ v2+…+ vk=1. Совокупность пар (yi; vi) называется рядом распределения относительных частот. данный ряд также удобнее представлять в виде таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
vi |
|
0,28 |
|
0,28 |
|
0,12 |
|
0,04 |
|
0,12 |
|
0,08 |
|
0,08 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Группировка.
При очень большом объеме выборки ее элементы объединяют в группы (классы), представляя результаты опытов в виде группированного статистического ряда. Для этого интервал, содержащий все значения выборки, разбивают на k непересекающихся интервалов (удобнее разбивать на равные интервалы). При этом считается, что правая граница интервала принадлежит следующему интервалу. Например:
|
|
|
|
|
|
|
|
|
yi |
|
17-19 |
|
19-21 |
|
21-23 |
|
|
|
|
|
|||
|
ni |
|
14 |
|
4 |
|
7 |
|
|
|
|
|
|||
|
vi |
|
0,56 |
|
0,16 |
|
0,28 |
|
|
|
|
|
|
|
|
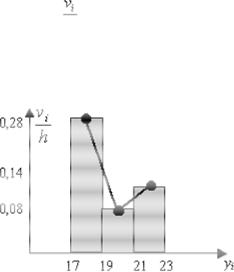
Для наглядного представления генеральной совокупности используется специальный график – гистограмма. Строится она следующим образом: пусть длина каждого маленького промежутка (интервала) равна h. Построим на i-м промежутке как на
основании прямоугольник высотой 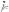

 . Ясно, что площадь каждого такого прямоугольника будет равна vi, а суммарная площадь всех прямоугольников равна 1.
. Ясно, что площадь каждого такого прямоугольника будет равна vi, а суммарная площадь всех прямоугольников равна 1.
Построенная гистограмма называется гистограммой относительных частот.

Если соединить отрезками середины верхних сторон прямоугольников гистограммы,
получится – полигон относительных частот.
Аналогично строятся гистограмма и полигон частот – высота прямоугольников равна
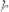
 , а суммарная площадь гистограммы равна n. Внешне гистограмма частот отличается от гистограммы относительных частот тем, что у нее каждый прямоугольник в n раз выше.
, а суммарная площадь гистограммы равна n. Внешне гистограмма частот отличается от гистограммы относительных частот тем, что у нее каждый прямоугольник в n раз выше.
***
Рассмотрим точечные оценки числовых параметров распределения. Пусть дана некоторая выборка: х1, х2, …, хn. Тогда выборочным средним называют величину:



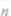 .(x1 + x2 + x3 +…+xn).
.(x1 + x2 + x3 +…+xn).
Если выборка задана рядом распределения частот:
xi 
 x1
x1 
 x2
x2 
 x3
x3 
 …
…
 xk ni
xk ni
 n1
n1
 n2
n2
 n3
n3
 …
…
 nk
nk
где n1+n2+…+nk=n, то для подсчета выборочного среднего приведенную выше формулу
можно преобразовать в следующий вид: (x1.n1+ x2.n2+ x3.n3+…+ xk.nk).
Выборочной дисперсией или мерой рассеяния значений признака Х по отношению к его выборочному среднему называют величину:
s2=  ( (x1-
( (x1- ) 2 +(x2-
) 2 +(x2-  ) 2 +…+(xn-
) 2 +…+(xn-  )2 ).
)2 ).
Если выборка задана рядом распределения частот:
xi x1 x2 x3 … xk ni n1 n2 n3 … nk
где n1+n2+…+nk=n, то для подсчета выборочной дисперсии приведенную формулу также удобно преобразовать:
s2= 
 (n1(x1-
(n1(x1-  ) 2+n2(x2-
) 2+n2(x2-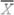 ) 2+…+nk(xk-
) 2+…+nk(xk-  )2).
)2).
Корень квадратный из дисперсии называют средним квадратическим отклонением:
s= 



 .
.
Пример.
Пусть выборка задана рядом распределения частот признака Х:
xi |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
ni |
7 |
7 |
3 |
1 |
3 |
2 |
2 |
Тогда:

 (17× 7+18× 7+19× 3+20× 1+21× 3+22× 2+23× 2)=
(17× 7+18× 7+19× 3+20× 1+21× 3+22× 2+23× 2)= 
 =19.
=19.

s2= 
 ((17-19)2× 7+(18-19)2× 7+(19-19)2× 3+(20-19)2× 1+(21-19)2× 3+(22-19)2× 2+(23-19)2×
((17-19)2× 7+(18-19)2× 7+(19-19)2× 3+(20-19)2× 1+(21-19)2× 3+(22-19)2× 2+(23-19)2×
2)= 
 =3,92.
=3,92.
s= 



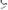


 =1,98.
=1,98.
***
С помощью методов вторичной статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом.
Для сравнения выборочных средних величин, принадлежащих к двум выборкам, и для решения вопроса о том, отличаются ли средние значения друг от друга достоверно, часто используют t-критерий Стъюдента. Основная формула данного критерия выглядит следующим образом:
,
где: 

 ,
, 
 ,
, 

 - выборочное среднее, выборочная дисперсия и число данных первой
- выборочное среднее, выборочная дисперсия и число данных первой
выборки данных; 

 ,
, 
 ,
, 

 - выборочное среднее, выборочная дисперсия и число данных второй выборки данных.
- выборочное среднее, выборочная дисперсия и число данных второй выборки данных.
После вычисления экспериментального значения критерия Стъюдента 



 , по таблице критических значений t-критерия Стъюдента для заданного числа степеней свободы, равного n1+n2-2, и избранной вероятности допустимой ошибки (обычно 0,05; 0,01 или
, по таблице критических значений t-критерия Стъюдента для заданного числа степеней свободы, равного n1+n2-2, и избранной вероятности допустимой ошибки (обычно 0,05; 0,01 или
0,001) находят нужное табличное значение 


 и сравнивают его с экспериментальным.
и сравнивают его с экспериментальным.
Если 








 , то делается вывод о том, что средние значения двух выборок данных действительно статистически различаются с вероятностью допустимой ошибки.
, то делается вывод о том, что средние значения двух выборок данных действительно статистически различаются с вероятностью допустимой ошибки.
Если 







 , то делается вывод о том, что различия средних значений двух выборок данных статистически не существенны.
, то делается вывод о том, что различия средних значений двух выборок данных статистически не существенны.
Примеры решения задач
Пример 4.А. Имеются данные о количестве успевающих на «4» и «5» студентов 20
групп некоторого вуза: 10, 12, 11, 15, 15, 9, 12, 14, 16, 13, 12, 13, 11, 17, 15, 16, 14, 13, 14, 14.
а) Найти объем выборки, размах выборки. Построить ряд распределения частот, ряд распределения относительных частот, группированный статистический ряд, гистограмму и полигон относительных частот.
б) Найти: выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение.
а)объем выборки n =20; размах выборки R =17–9=8. Построим ряд распределения частот:

xi |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
ni |
1 |
1 |
2 |
3 |
3 |
4 |
3 |
2 |
1 |
Построим ряд распределения относительных частот |
|
||||||||
xi |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
vi |
0,05 |
0,05 |
0,10 |
0,15 |
0,15 |
0,20 |
0,15 |
0,10 |
0,05 |
Построим группированный статистический ряд (h=3):
xi 9-12 12-15 15-17 ni 4 10 6 vi 0,20 0,50 0,30
Гистограмма и полигон относительных частот будут выглядеть следующим образом:
б) Выборочное среднее |
(9.1 +10.1 +11.2 +12.3+ +13.3 +14.4+15.3+16.2+17.1) = |
=13. |
|
Выборочная дисперсия s2= 

 ((9-13)2.1 +(10-13)2.1 +(11-13)2.2 +(12-13)2.3 +(13-13)2.3 +(14-13)2.4 +(15-13)2.3+(16-13)2.2+(17-13)2.1) = 4,21.
((9-13)2.1 +(10-13)2.1 +(11-13)2.2 +(12-13)2.3 +(13-13)2.3 +(14-13)2.4 +(15-13)2.3+(16-13)2.2+(17-13)2.1) = 4,21.
Среднее квадратическое отклонение s= |
=2,05. |
Пример 4.Б. Экспериментальным путем получены две выборки данных: 3; 4; 5; 3; 2; 3; 3; 2; 5; 4 и
5; 5; 3; 4; 4; 3; 5; 3; 6; 4. Существенно ли отличаются средние значения этих выборок, если 

 =2,10 (для числа степеней свободы = 18 и вероятности допустимой ошибки = 0,05)?
=2,10 (для числа степеней свободы = 18 и вероятности допустимой ошибки = 0,05)?
Для первой выборки: 

 =10;
=10; 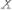
 =3,4;
=3,4; 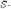
 =1,04.
=1,04.
Для второй выборки: 
 =10;
=10; 

 =4,2;
=4,2; 
 =0,96.
=0,96.
Найдем экспериментальное значение t-критерия Стъюдента:



 =1,79<2,10. Поскольку
=1,79<2,10. Поскольку 







 различия средних значений двух выборок не существенны.
различия средних значений двух выборок не существенны.

Задания для самостоятельного решения
4.1.Имеются данные об итоговой сумме баллов тридцати абитуриентов: 12, 15, 20, 17, 16, 18, 18, 19, 19, 14, 16, 13, 12, 13, 13, 15, 16, 14, 14, 16, 17, 12, 15, 16, 15, 12, 13, 13, 15, 17.
Найти объем выборки, размах выборки. Построить ряд распределения частот, ряд распределения относительных частот, группированный статистический ряд, гистограмму и полигон относительных частот.
4.2.Имеются данные о количестве студентов в 24 группах:
28, 27, 26, 28, 27, 25, 22, 24, 25, 23, 24, 25, 22, 21, 23, 19, 20, 21, 22, 19, 21, 20, 22, 18.
Найти объем выборки, размах выборки. Построить ряд распределения частот, ряд распределения относительных частот, группированный статистический ряд, гистограмму и полигон относительных частот.
4.3. Дан ряд распределения учащихся 11 класса по уровням сформированности математических знаний:
xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
ni |
1 |
3 |
5 |
7 |
11 |
13 |
8 |
1 |
1 |
Найти: выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение. 4.4. Дан ряд распределения студентов 1 курса по размерам обуви:
xi |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
ni |
3 |
5 |
6 |
13 |
10 |
7 |
4 |
2 |
Найти: выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение. 4.5. Среди 10 студентов было проведено два опроса, целью которых было выявление уровня знаний по предмету (по 10-балльной шкале) в начале и конце учебного года. В результате были
получены две выборки данных: 4; 5; 3; 5; 5; 5; 4; 5; 6; 3 (в начале года) и 6; 8; 4; 5; 6; 7; 4; 5; 7; 5 (в
конце года). Существенно ли отличие в уровне знаний студентов в начале и конце года, если 

 = 2,10 (для числа степеней свободы = 18 и вероятности допустимой ошибки = 0,05)?
= 2,10 (для числа степеней свободы = 18 и вероятности допустимой ошибки = 0,05)?
От математики к информатике
По данным из заданий 4.1 и 4.2 построить гистограмму и полигон относительных частот при помощи электронных таблиц Excel из пакета Microsoft Office.
По данным из заданий 4.3 и 4.4 рассчитать выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение при помощи электронных таблиц Excel из пакета Microsoft Office.
По данным из задания 4.5 рассчитать экспериментальное значение критерия Стъюдента при помощи электронных таблиц Excel из пакета Microsoft Office.
Литература
Основная
5.Виленкин Н.Я., Пышкало А.М., Рождественская В.Б. Математика. – М.: Просвещение, 1997.
6.Виленкин Н.Я. и др. Математика: Учебное пособие для студентов педагогических институтов. - М.: Просвещение, 1977.
7.Виленкин Н.Я., Лаврова Н.Н., Рождественская В.Б. Задачи и практикум по математике. - М.: Просвещение, 1977.
8.Гмурман В.Е. Руководство по решению задач по теории вероятностей и математической статистике: Учебное пособие для втузов. – М.: Высшая школа, 1979.
9.Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. – М.:
Наука, 1982.
10.Пышкало А.М., Стойлова Л.П., Лаврова Н.Н. Сборник задач по математике. - М.: Просвещение, 1979.
11.Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: Речь, 2000.
12.Солодовников А.С. Теория вероятностей: Учебное пособие для студентов педагогических институтов. – М.: Просвещение, 1983.
13.Стойлова Л.П., Виленкин Н.Я., Лаврова Н.Н. Математика. Ч.1. - М.: Просвещение, 1990.
14.Стойлова Л.П., Пышкало А.М. Основы начального курса математики. - М.: Просвещение, 1988.
Дополнительная
15.Шафрин Ю.А. Основы компьютерной технологии.- М., 1997.
16.Стинсон К. Эффективная работа в Windows 95: Перев. с англ. - СПб, 1997.
17.Борланд Р. Эффективная работа с Microsoft Word 7.0.: Перев. с англ. - СПб, 1997.
18.Додж М., Кината К., Стинсон К. Эффективная работа с Microsoft Excel 7.0.: Перев. с англ. - СПб, 1997.
19.Симонович С.В., Евсеев Г.А., Алексеев А.Г. Общая информатика: Учебное пособие для средних школ. – М.: АСТ-ПРЕСС,1998.
