Алгоритмы селекции отметок в стробах.

При решении задачи селекции отметок могут быть ис­пользованы два способа продолжения траектории сопровождаемой це­ли. Оба способа базируются на статистических различиях в вагонах движения реальных и ложных целей.

Суть первого способа состоит в том, что траектория продолжается по каждой из попавшей в строб отметок (рис.2.2О). Это приводит к "разветвлению" траектории, причем часть ее ветвей являют­ся ложными (на рис.2.20 они показаны пунктиром). Однако ответв­ления траектории, построенные по ложным отметкам, вскоре должны быть сброшены с сопровождения из-за отсутствия корреляции между такими метками в последующих обзорах РЛС. Траектория же, постро­енная по реальным отметкам (точки А_1(к-1), А_1к, А_1(к+2) на рис.2.20), будет продолжена. Данному способу селекции отметок присущи существенные недостатки: в связи с необходимостью сопровождать, хотя и кратковременно, ложные цели значительно повышаются требования к производительности ЦВМ ВОИ; "засорение" индикаторных устройств пунктов управления трассами ложных целей резко увеличивает психологическую нагрузку на бо­евой расчет АСУ.

При втором способе из всех отметок, попавших в строб, выбира­ется одна, вероятность принадлежности которой к сопровождаемой траектории наибольшая. Остальные отметки отбрасываются как лож­ные. Так как на практике чаще применяется второй способ продолже­ния траекторий, то в дальнейшем рассматриваются методы селекции отметок в стробах, основанные на этом подходе.

По своей сущности задача селекции отметок представляет задачу проверки двух взаимно исключающих гипотез Н_о и Н₁ для каждой из q попавших в строб отметок. Гипотеза Н_о состоит в том, что j-я отметка, отклонения координат которой от центра строба равны ΔX_j, ΔY_j (j-1,q), является ложной. Альтернативная ей гипотеза Н₁ сос­тоит в том, что j-я отметка принадлежит сопровождаемой цели. В Результате проверки гипотез по всем q отметкам должно быть принято решение о том, какую из отметок следует считать продолжением траектории.

Если известны функции правдоподобия L (ΔX_j, ΔY_j /Н₁) и L (ΔX_j, ΔY_j /Н_о), то решение задачи селекции отметок сводится к испытанию отношения правдоподобия λ(Х), то есть к проверке условия:

(2. 28).

Пороговое значение φ может быть выбрано в соответствии с одним из известных методов принятия статистических решений, например, исходя из нежелательности попадания ложных отметок в строб, или, что то же самое, из условия достижения минимума ошибки принятия решения о принадлежности j-й отметки к сопровождаемой трасе, когда на самом деле отметка является ложной (критерий Найма - Пирсона).

При высказанном выше смысловом содержании гипотез Н₁ и Н_о отношение функций правдоподобия отклонений реальных и ложных отметок L (ΔX_j, ΔY_j /Н₁) и L (ΔX_j, ΔY_j /Н_о) характеризуется отношением плотностей распределения W_ц(ΔX_j,ΔY_j) W_μ(ΔX_j,ΔY_j) Тогда отношение (2.28) может быть записано в виде:

(2.29).

Подставив выражение для плотностей вероятностей (2.26) и (2.27) в отношение (2.29), получим

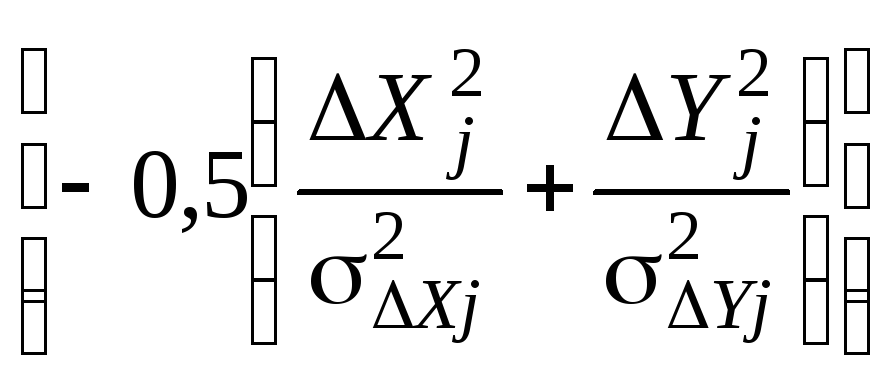
ехр (2.30).

Проанализировав соотношение (2.30), можно сделать важный для дальнейшего изложения вывод: при известных (фиксированных) значе­ниях ошибок измерения и экстраполяции координат сопровождаемых целей δ_Δx, δ_Δy и заданной средней плотности ложных отметок для максимизации отношения правдоподобия необходимо минимизировать величину

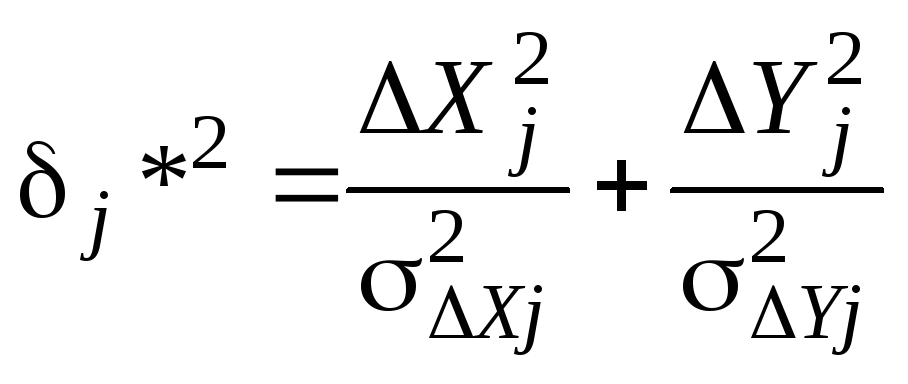(2.31).

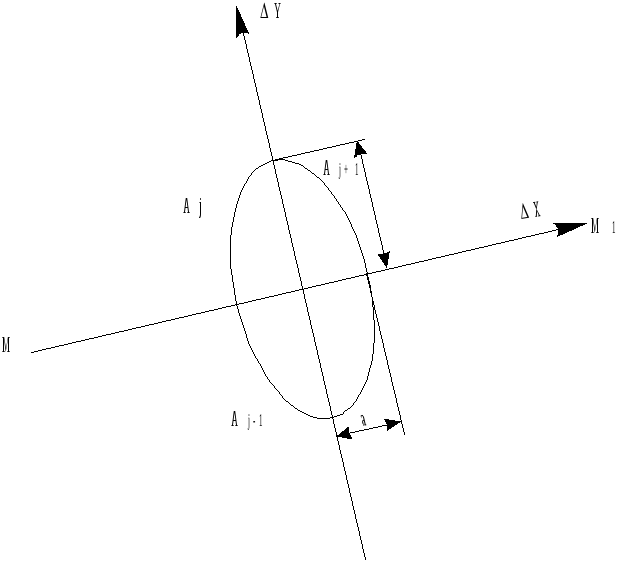
Данное выражение представляет собой уравнение эллипса равных вероятностей (эллипса рассеивания), центр которого совпадает с центром строба. Поэтому отклонения отметок от центра строба σ*j, принято называть суммарными эллиптическими отклонениями. Эллипс рассеивания сориентирован таким образом, что направление одной главной оси рассеивания совпадает с экстраполированной трассой (прямая ММ1), а вторая ось перпендикулярна этому направлению (рис.2.21).

Л

Рис. 2.21. Эллипс равных вероятностей.

юбым точкам А_j-1, А_j, Аj=1..., лежащим на эллипсе вида (2.31) соответствуют одинаковые значения плотности распределения W_ц(ΔX,ΔY). С уменьшением величины отклонения увеличивается значение функции W_ц(ΔX,ΔY) и естественно, возрастает вероятность принадлежности отметки А_j к сопровождаемой трассе. На этом поло­жении основываются алгоритмы селекции отметок, досмотрим некото­рые из применяемых в алгоритмах ВОИ методов селекции отметок по их отклонениям от центра строба.