ФИЗИКА(лабы,модули) / описание лабораторных работ / Лр8

ЛАБОРАТОРНАЯ РАБОТА N-6

ОПРЕДЕЛЕНИЕ момента инерции КАТАЮЩЕГОСЯ ШАРИКА.

ЦЕЛЬ РАБОТЫ : изучить законы движения катающегося по сферической вогнутой поверхности шарика , рассмотреть условия его гармонических колебаний, определить момент инерции шарика и исследовать зависимость момента инерции от радиуса шарика.

ПРИБОРЫ И ОБОРУДОВАНИЕ : вогнутая сферическая поверхность , шарики , секундомер , микрометр, штангенциркуль, линейка.

КРАТКАЯ ТЕОРИЯ : Радиус кривизны R гладкой сферической поверхности можно определить , измерив период колебания Т шарика , катающегося по этой поверхности .

Если пренебречь потерями энергии , затрачиваемой на преодоление диссипативной силы трения , то для катающегося без проскальзывания шарика , должен выполнятся закон сохранения механической энергии . Центр масс С шарика движется поступательно , но , кроме того , шарик вращается относительно оси Z , проходящей через точку С перпендикулярно плоскости рисунка ( 1 )

Поэтому полная механическая энергия шарика :

( 1 )

Здесь m - масса шарика ;

— его момент инерции относительно оси Z;

r - радиус шарика .

Рис.1

Модуль угловой скорости вращения шарика вокруг оси Z , связан с модулем скорости поступательного движения центра масс соотношением :

( 2 )

Подставляя ( 2 ) и выражение для J_c в ( 1 ) , получаем :

( 3 )

Но , при качении шарика по сферической поверхности , его центр масс отклоняется относительно центра О поверхности на угол . Из рисунка ( 1 ) , видно , что угол связан с углом поворота шарика относительно оси Z соотношением :

( 4 )

где R`= R-- r

Кроме того , из прямоугольного треугольника ОВС следует , что :

( 5 )

Подставляя ( 4 ) и ( 5 ) в формулу ( 3 ) , выражаем полную механическую энергию шарика через угол :

( 6 )

В верхней точке траектории скорость шарика равна нулю и вся механическая энергия шарика переходит в потенциальную . При прохождении шариком положения равновесия () скорость и кинетическая энергия шарика максимальны .

Рассмотрим кинематику движения шарика . Скорость его центра масс С всегда направлена по касательной к траектории ( рис.2 ) . Полное ускорение центра масс равно сумме тангециального и нормального ускорений .

Ускорение направлено также по касательной к траектории . Его модуль связан с модулем углового ускорения вращения шарика вокруг оси Z формулой

( 7 )

Ускорение направлено к центру кривизны . Его модуль ( 8)

Эти модули изменяются при колебательных движениях шарика периодически . В верхней точке траектории при небольшом отклонении шарика от положения равновесия , V_c шарика и равны нулю, а a_t достигает максимума . При прохождении положения равновесия , наоборот , a_t=0 , a V_c и a_n максимальны .

Найдем период колебаний шарика . Для этого необходимо получить динамическое уравнение колебаний ( т.е. уравнение динамики для поступательного или вращательного движения колеблющегося шарика ) . Для любых незатухающих гармонических колебаний это уравнение имеет общий вид

( 9 )

Физическое тело будет совершать гармонические колебания в том случае , если на него действует сила или момент силы , пропорциональные смещению от положения равновесия и стремящиеся вернуть тело в положение равновесия .

Воспользуемся законом сохранения механической энергии ( 6 )­ .

Возьмем производную по времени от обеих частей этого уравнения и сократим полученное выражение на ( )

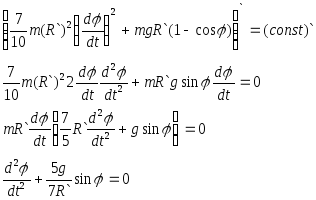( 10 )

Отсюда видно , что шарик будет совершать гармонические колебания относительно положения равновесия в том случае , когда ( ) . Т.е. условием гармонических колебаний в данной работе будут малые углы отклонения шарика от положения равновесия .

Cравнивая уравнения ( 9 ) и ( 10 ) замечаем , что , с другой стороны , тогда:

( 12 )

При вычислении мы не учитывали , что механическая энергия шарика уменьшается за счет работы диссипативной силы трения и потому в действительности колебания шарика будут затухающими .

Радиус кривизны вогнутой сферической поверхности можно определить , измеряя с помощью штангециркуля и линейки величины а , R , h приведенные на рисунке 3.

Период колебаний шарика определяем измерив время нескольких (5-10)

его колебаний.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

1. С помощью микрометра не менее трех раз измерить диаметр шариков d и

вычислить радиус .

2. Вывести шарик из положения равновесия , определить время t 5-10 ( по укозанию преподавателя ) полных колебания шарика . Опыт провести не менее пяти раз . Определить период колебаний . Занести данные в таблицу 1 .

3. Вычислить среднее значение радиуса шарика < r > , периода колебаний < T > ,

радиуса кривизны поверхности <R>, и, подставляя их в расчетную формулу (7),

определить момент инерции шарика. Плотность материала шарика --взять равной плотности стали: 7,810³ кг/м³.

5. Опыт повторить для 5 шариков различных радиусов и построить график зависимости J=f(r).

6. Найти относительную погрешность и доверительный интервал определения момента инерции шарика.

7.Рассчитать момент инерции шарика по формуле J=2/5mr².

8. Сравнить результаты полученные двумя способами .

9. Данные измерений и расчетов занести в таблицы 1-3 .

10. Записать вывод по работе.

таб. 1.

d , м					< d > , м		< r > , м

таб. 2.

t1 , c	n1	Ti , c	Ti , c	( Ti )2 , c2

таб. 3.

Т , c	T , c	r , м	r , м	J1 кг.м2	J2 кг.м2	%	

ВОПРОСЫ И УПРАЖНЕНИЯ .

1.Из каких составляющих складываются полная механическая энергия шарика ?

2. Когда выполняется закон сохранения полной механической энергии ?

3. Как движется центр масс шарика ?

4. Где ось вращения шарика ?

5. Как направлены скорость и ускорение центра масс шарика ?

6. Укажите положение шарика , в которых его центр будет иметь :

а) максимальное угловое ускорение .,

б) максимальную линейную скорость.

в) тангециальное ускорение , равное нулю.

г) нормальное ускорение равное нулю .

д) угловое ускорение равное нулю .

7. Какой вид имеет динамическое уравнение колебаний шарика ? Объясните его смысл .

8. Сформулируйте условия , при которых возникают гармонические колебания .

9. Почему угол отклонения шарика от положения равновесия в данной работе должен быть мал ?

10. Определите вес шарика в нижней точке поверхности.

11. Сравните периоды колебаний разных шариков и объясните наблюдаемую закономерность.

12. Выведите формулу для расчета момента инерции шарика.

ЛИТЕРАТУРА : Савельев И.В. Курс общей физики -2-е изд.-М:Наука ;1986-Т.1 гл.1 , пар.4 ,гл 3 пар.24 , гл.5 пар.41-43, пар.53