12. Типовые законы регулирования. Типовые передаточные функции автоматических регуляторов

Задача регулятора- определение текущей ошибки регулирования и генерация соответствующего регулирующего воздействия, направленного на устранение этой ошибки.

Закон регулирования– зависимость между входной и выходной величинами регулятора составленного без учета инерционности его элементов

Существует всего 5 основных типов регуляторов:

• Пропорциональный

• Интегральный

• Пропорционально-Интегральный (изодромный)

• Пропорционально-Дифференциальный

• Пропорционально-Интегрально-Дифференциальный

Пропорциональные регуляторы (П-регуляторы)

Осуществляют регулирование по закону:

Передаточная функция такого элемента имеет вид:

Его достоинство – быстродействие, недостаток – наличие статической ошибки регулирования.

Интегральные регуляторы (И-регуляторы)

Регулируют по закону:

Передаточная функция:

гдеT_u– постоянная времени такого регулятора (ее, кстати, может и не быть).

И-регуляторы воздействуют на ОУ до полного исключения установившейся ошибки.

Их недостаток – несколько сниженное, по сравнению с П-регуляторами, быстродействие.

Пропорционально-Интегральные Регуляторы (ПИ-регуляторы)

Осуществляют коррекция по закону:

Передаточная функция имеет вид:

Величина регулирующего воздействия здесь пропорциональна времени существования ошибки регулирования.

При необходимости, регулирующее воздействие сначала скачкообразно прыгает на величину k*r₀за счет пропорциональной составляющей, а затем в дело вступает интегральная часть и воздействие начинает плавно возрастать до полного устранения ошибки регулирования.

Если принять что Tu– бесконечно большая величина, то получим ПИ-регулятор, а если принятьkиTuбесконечно малыми, но их отношение существенные, получим И-регулятор с коэффициентом передачи

Пропорционально-Дифференциальные Регуляторы (ПД-регуляторы)

Закона регулирования, однако, выглядит так:

Регуляторы этого типа реагируют не только на саму ошибку, но и на скорость ее решения.

ЗЫ: «А почему бы не сделать просто дифференциальный регулятор» - спросит Харькин.

«А потому» - должен ответить Ты – «что такой регулятор станет реагировать только на скорость изменения ошибки, а не на ее наличие»

Пропорционально-Интегрально-Дифференциальные Регуляторы (ПИД-регуляторы)

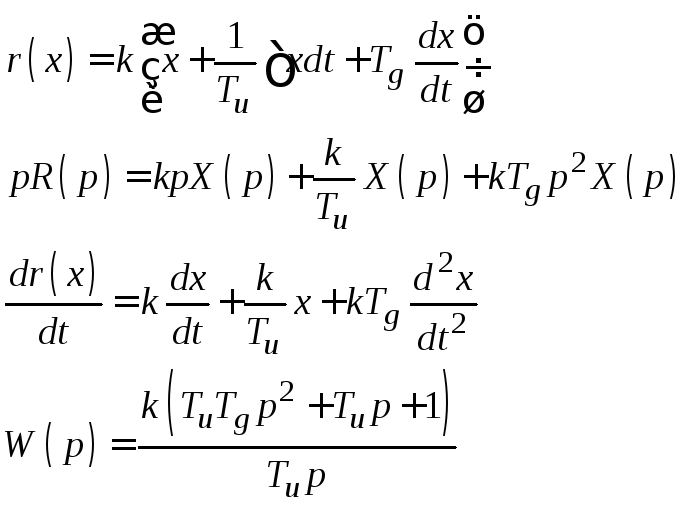
• Если принять Tuдостаточно большим, аTg– достаточно малым (под ноль), получим П- регулятор

• Tg=0 и малыеkиTu(при нормальном соотношенииk/Tu) дадут И-регулятор

• При достаточно больших Tg=0,kиTuу нас будет ПИ-регулятор

• А при больших Tu=бесконечность,kиTgв наших руках окажется вещь по имени ПД-регулятор

13. Получение и построение частотных характеристик. Построение афх разомкнутой системы. Связь между частотными характеристиками разомкнутой и замкнутой систем.

Частотные характеристики соединительных звеньев и разомкнутых систем.

W(p)=W₁(p)* W₂(p)* W₃(p)

W(jw)=W₁(jw)* W₂(jw)* W₃(jw)

W(w)= e^jφ(w)=W₁(w)e^jφ1(w)*W₂(w)e^jφ2(w)*W₃(w)e^jφ3(2)

W(w) e^jφ(w)=W₁(w)*W₂(w)*W₃(w)* e^{j(φ1(w)+ φ2(w)+ φ3(w))}

W(w)= W₁(w)*W₂(w)*W₃(w)

φ(w) =φ₁(w)+ φ₂(w)+ φ₃(w)

20lgW(w)=20lgW₁(w)+20lgW₂(w)+20lgW₃(w)

L(w)=L₁(w)+ L₂(w)+ L₃(w)

Example:

W(p)=10/(p(0,1p+1)); W(jw)=10/(jw(0,1jw+1))= -10/(0,1w²-jw)= -10(0,1w²+jw)/(0,01w⁴+w²)

U(w)= -w²/(0,01w²+w²)=-1/(0,01w²+1)

V(w)=-10/(0,01w⁴+w²)

w=0 U(0)=1 V(0)= -∞

w=∞ U(∞)=0 V(∞)=0

w=∞ 10(w=0)

-1 w=∞ +

φ₁

φ₁-π/2

w>0w>0

Частотные характеристики замкнутых систем.

W(p)=B(p)/A(p)

W(jw)=B(jw)/A(jw)=U(w)=jV(w)

W(w)e^jφ(w)=W(w)(cosw+jsinw)

Ф(p)=W(p)/(1-W(p)); Ф(jw)=W(jw)/(1+W(jw))

Передаточная функция замкнутой системы заданной апериодической функцией:

Ф(jw)=W(jw)/(1+W(jw))=(U(w)+jV(w))/(1+U(w)+jV(w))=U(w)(1+U(w)+V²(w))/(1+U²(w)+V²(w))

V_ф(w)=Y(w)/((1+U(w))²+V²(w))

Ф(w)=(U_ф²+V_ф²)^1/2

φ_ф(w)=arctg(V_ф(w)/U_ф(w))

Ф(w)=([U(w)(1+U(w))+V²(w)]²±V²(w))^1/2/((1+U(w))²+V²(w))

φ(w)=arctg(V(w)/((1+U(w))²+V²(w))

W(jw)=W(w)e^jφ(w)

Нанограмма замыкания

В практике ТАУ переход от частотной характеристики разомкнутых систем к частотным характеристикам замкнутых систем осуществляется с помощью круговых диаграмм.

Эти диаграммы позволяют по частотным характеристикам разомкнутой системы получить вещественные и мнимые частотные характеристики замкнутой системы, ЛЧХ разомкнутой и замкнутой систем.

Нанограммы охватывают значение L(0;+28)дБ; (0; -26)дБ

Для больших по абсолютной величине значения надобности нанограмме отпадает, т. к. в этом случае Lзамкнутой системы будет равно нулю и φ замкнутой системы равно нулю,

если L>20дб=>L_зам.=L_разом.;φ_зам=φ_разом, еслиL<20дб.