4. Явление электромагнитной индукции. Основной законэлектромагнитной индукции. Правило (закон) Ленца. Самоиндукция. Энергия магнитного поля. Объемная плотность энергии магнитного поля.

Электромагнитная индукция – возникновение электродвижущей силы (эдс индукции) в проводящем контуре, находящемся в переменном магнитном поле или движущимся в постоянном магнитном поле.

ЭДС возникающую в проводниках при изменении магнитного потока называют электродвижущей силой (ЭДС) электромагнитной индукции E_i, а ток в замкнутом проводнике – индукционным. ЭДС электромагнитной индукции является распределенной в отличие от ЭДС источника тока, которую называют сосредоточенной.

Основной закон электромагнитной индукции (закон Фарадея):

"При пересечении потока магнитной индукции отрезком проводника в последнем возникает ЭДС электромагнитной индукции, прямо пропорциональная скорости изменения величины магнитного потока."

E_i,

где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин;

dФ/dt – скорость изменения магнитного потока.

В системе СИ k=1значитE_i =-

Правило Ленца: "Индукционный ток всегда направлен так, чтобы своим действием препятствовать причине его порождающей или индукционный ток направлен так, что создаваемое им поле препятствует изменению магнитного потока".

Дифференциальная форма закона электромагнитной индукции

rotE=-dB/dt.

Самоиндукция – явление возникновения ЭДС электромагнитной индукции в каком-либо контуре вследствие изменения магнитного потока, создаваемого электрическим током этого контура.

Величина ЭДС самоиндукции определяется по общей формуле, выражающей основной закон электромагнитной индукции

E_с=-dФ/dt.

ЭДС самоиндукции, возникающая в бесконечно длинном соленоиде



где L= ₀n²S=₀n²V=(₀N²S)/– коэффициент самоиндукции или индуктивность соленоида.

Индуктивность L зависит от формы, размеров проводника и магнитной проницаемости среды, окружающей проводник.

При di/dt=1 А/с:

Индуктивность (коэффициент индуктивности) – физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при скорости изменения тока в нем равной 1 А/с.

При L=const E_с=-Ldi/dt.

Если L const, что возможно при=f(H)



Связь потока магнитной индукции с током в проводнике

Ф=Li.

Взаимная индукция, явление, в котором обнаруживается магнитная связь двух или более электрических цепей. Благодаря этой связи возникает ЭДС индукции в одном из контуров при изменении тока в другом. Количественной характеристикой магнитной связи электрических цепей является взаимная индуктивность.

При включении источника с ЭДС Eв цепь, состоящую из сопротивления R и соленоида с индуктивностью L, которые соединены последовательно, сила тока в цепи возрастает согласно закону

i=E/R-E/Rexp(-Rt/L)=E/R[1-exp(-Rt/L)],

т.е. ток постепенно возрастает от i=0 до i=E/R при t.

При выключении постоянного источника сторонних ЭДС, сила тока уменьшается согласно уравнению:

i(t)=E/R[exp(-Rt/L)].

За время нарастания, убывания силы тока в цепи принять такое значение t, при котором показатель экспоненты обращается в минус единицу, т.е. t=L/R.

Закон Ома, при наличии в цепи конденсатора и сопротивления, записывается в виде уравнения IR=U₀-q/C,

где q – заряд на обкладке конденсатора;

q/C – разность потенциалов между обкладками конденсатора.

При выключении постоянной ЭДС из цепи, с емкостью и сопротивлением, изменение тока в цепи подчиняется уравнению

,

при включении

.

Время убывания, возрастания тока в цепи определяется соотношением

t=RC.

В общем случае, когда цепь состоит из емкости C, индуктивности L, сопротивления R и источника тока с ЭДС E, уравнение для тока в цепи имеет вид



Энергия магнитного поля: W=.

Энергия магнитного поля двух контуров с током



В случае N контуров:



где L_ik– при i=k называется индуктивностью i-го контура, а при ik – взаимной индуктивностью i-го и k-го контуров.

Величину Lik можно определить по формуле



где d_i, d_k– элементы i-го и k-го контуров;

r_ik– расстояние между ними.

Энергия магнитного поля соленоида



где V=S– объем соленоида, заполненный однородным магнитным полем.

Объемная плотность энергии магнитного поля – энергия поля отнесенная к его объему, т.е. объёмная плотность энергии магнитного поля – физическая величина, которая показывает, какой энергией обладает магнитное поле, занимающее единицу объема пространства:

w_o=W/V.

Объемная плотность магнитного поля длинного соленоида



В неоднородном магнитном поле, энергия dW магнитного поля элемента объема dV, равна:

dW=w_odV.

Энергию неоднородного магнитного поля, занимающего какой-либо объем пространства, можно определить по формуле:



4.1. Примеры решения задач.

4.1.1. В однородном магнитном поле с индукцией 10,010^-2Тл расположена прямоугольная рамка (контур) abcd, подвижная сторона которой ad длиной==0,10 м перемещается со скоростью v=25 м/с перпендикулярно линиям индукции поля. Определить ЭДС индукции, возникающую в контуре.

Решение. При движении проводника ad площадь рамки увеличивается, магнитный поток Ф сквозь рамку возрастает, а значит, согласно закону Фарадея, в рамке должна при этом возникать ЭДС индукции. Чтобы ее определить, сначала выразим магнитный поток Ф через индукцию поля B и стороны рамки, x (x – расстояние от bc до ad. Согласно формуле



имеем Ф=BS=Bx.

Подставив это значение Ф в формулу E=– dФ/dt и учитывая, что B,– величины постоянные, запишем

E=– dФ/dt=-Bl(dx/dt),

где v=dx/dt – скорость перемещения проводника ad. Поэтому

E=-Blv. (1)

Размерность полученного результата очевидна.

Сделав подстановку числовых значений величин B, , v (все даны в единицах системы СИ), получим ответ

E=– 10,010^-20,1025=-2,510^-2В.

Ответ: E=-2,510^-2В.

Знак "минус" в формуле (1) показывает, что ЭДС индукции действует в контуре в таком направлении, при котором связанная с ним правилом правого винта нормаль к контуру противоположна вектору B. Отсюда заключаем, что и индукционный ток направлен в данном контуре против часовой стрелки. К такому же результату придем, применив правило правой руки для проводника ad.

Заметим, что если бы проводник ad двигался влево, то положительному приращению времени соответствовало бы отрицательное приращение (убыль) величины x. В этом случае индукционный ток направлен по часовой стрелке.

Замечание. При решении задачи допущена неточность: не принималось в расчет магнитное поле, созданное индукционным током. Это поле образует некоторый поток Ф' сквозь рамку. При движении проводника ad поток Ф' изменяется, что приводит к появлению дополнительной ЭДС Очевидно, что этот эффект тем слабее, чем меньше сила тока. Поскольку она обратно пропорциональна сопротивлению цепи, можно утверждать, что решение задачи верно при условии достаточно большого сопротивления цепи.

4.1.2.Короткая катушка, содержащая N=10³витков, равномерно вращается с частотой n=10 с^-1относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям однородного магнитного поля (B=0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол=60⁰c линиями поля. Площадь катушки S=100 см².

Решение. Мгновенное значение ЭДС индукцииE_iопределяется основным уравнением электромагнитной индукции Фарадея-Максвелла

E_i=-d/dt, (1)

где =NФ – потокосцепление;

N – число витков катушки;

Ф – магнитный поток, пронизывающий каждый виток катушки.

Подставив выражение в формулу (1), получим

E_i=-. (2)

При вращении катушки магнитный поток Ф, пронизывающий катушку в момент времени t, изменяется по закону

Ф=BScost

где B – индукция магнитного поля

S-площадь сечения катушки

 – угловая скорость вращения

Подставив в формулу (2) выражение магнитного потока Ф и продифференцировав по временинайдём мгновенное значение ЭДС индукции

E_i=NBSsint

Заметив, что угловая скорость связана с частотой вращения n катушки соотношением=2n и что уголt=/2 –, получим (учтено, что sin(/2 –)==cos)

E_i=2nNBS.cos. (3)

Выразив величины, входящие в полученное соотношение, в единицах системы СИ, подставив их в формулу (3), и выполнив вычисление, получим

E_i=23,141010³0,0410^-20,5=25 В.

Ответ: E_i=25 В.

4.1.3. Квадратная проволочная рамка со стороной а=5 см и сопротивлением R=10 мОм находится в однородном магнитном поле (B=40 мТл). Нормаль к плоскости рамки составляет угол=30⁰с линиями магнитной индукции. Определить заряд, который пройдет по рамке, если выключить магнитное поле.

Решение. При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции

E_i=-dФ/dt.

Возникшая ЭДС индукции вызовет в рамке индукционный ток, мгновенное значение которого можно определить воспользовавшись законом Ома для полной цепи I_i=E_i/R,

где R – сопротивление рамки.

Тогда (1)

Так как мгновенное значение силы индукционного тока I_i=dQ/dt, то выражение (1) можно переписать в виде

,

откуда dQ=– dФ/R. (2)

Проинтегрировав (2), найдем

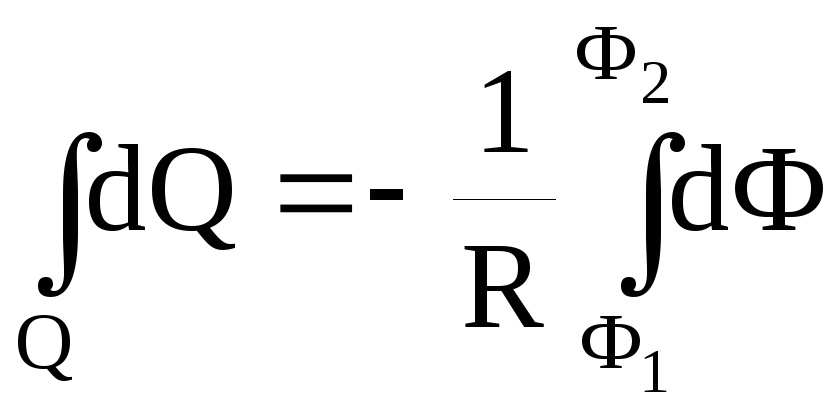
 тогда Q=(Ф₁-Ф₂)/R

Заметив, что при выключенном поле (конечное состояние) Ф₂=0, последнее равенство перепишем в виде

Q=Ф₁/R. (3)

Найдем магнитный поток Ф₁. По определению магнитного потока имеем

Ф₁=BScos,

где S – площадь рамки.

В нашем случае (рамка квадратная) S=а².

Тогда

Ф₁=Bа²cos. (4)

Подставив (4) в (3), получим

Q=(Bа²cos)/R.

Выразив величины, входящие в полученное соотношение, в единицах системы СИ, подставив их, и выполнив вычисление, получим



Ответ: Q=8,710^-3Кл.

4.1.4. В однородном магнитном поле с индукцией B вращается в плоскости, перпендикулярной линиям индукции, медный диск радиуса r, совершая n оборотов в секунду. При помощи скользящих контактов диск подключен к цепи, сопротивление которой R. Определить ЭДС индукции, возникающую при вращении диска, количество электричества q, протекающего по цепи, а также количество теплоты Q, выделенное в цепи за время, в течение которого диск совершил N оборотов.

Решение. При вращении диска в магнитном поле в контуре abcd, состоящем из цепи с сопротивлением R возникает индукционный ток, а значит, возникает ЭДС электромагнитной индукции. Так как магнитный поток сквозь этот контур не меняется, то, следовательно, закон Фарадея для электромагнитной индукции не может дать правильного результата. При движении проводников в магнитном поле закон Фарадея применяется лишь для контура, проходящего через одни и те же точки движущегося проводника. Здесь же участок контура проходит все время через различные радиусы вращающегося диска.

В контуре должна возникать ЭДС, так как один из его участков, например ad, представляет собой движущийся проводник, и поэтому на его свободные электроны, движущиеся вместе с диском, действуют силы Лоренца. Эти силы будут перемещать электроны относительно диска от точки a к точке d. Поэтому, чтобы найти ЭДС индукции, воспользуемся формулой определяющей любую ЭДС

E=

В данном случае в качестве сторонней силы, действующей только на участке ad, выступает сила Лоренца, численное значение которой равно:

F_л=еvBsina=еvB,

где е – заряд электрона.

E(1)

Интегрирование проводится не по замкнутому контур L, а только по длине участка ad, которая меняется от нуля до r.

Находясь в различных точках участка ad, электроны имеют разную линейную скорость v, но одинаковую угловую скорость . Для электрона, находящегося на расстоянииот центра диска, v==2n.

Подставив это значение v в формулу (1), получим

E. (2)

Таким образом, при равномерном вращении диска, в цепи действует постоянная ЭДС, создавая в ней постоянный ток.

Количество электричества q, перемещенное индукционным током, определяется формулой q=-Ф/R.

Однако последняя формула имеет смысл только в тех же случаях, что и закон Фарадея. Поэтому величину q можно определить, воспользовавшись известным соотношением для цепи постоянного тока:

q=It=Et/R.

Подставив вместо Eее значение по формуле (2) и учитывая, что t=N/n, найдем

q=r²NB/R. (3)

Количество теплоты Q, выделенное в цепи постоянного тока, с учетом формул (2), (3) выразим так

Q=EIt=Eq=²r⁴nNB²/R.

Из полученных результатов видно, что при заданном числе оборотов величина q не зависит от скорости вращения диска, тогда как величина Q, будучи пропорциональной n, зависит.

Замечание.При решении задачи в качестве сторонних сил, действующих на свободные электроны во вращающемся диске, рассматривалась лишь сила Лоренца. Строго говоря, надо учесть еще центробежные силы инерции (если рассматривать явление в системе отсчета, связанной с вращающимся диском). Эти силы действуют на электроны независимо от магнитного поля, отбрасывая их к краям диска и создают добавочную ЭДС Таким образом, в рассматриваемом случае имеется, по существу, два генератора ЭДС: один электромагнитный, второй "инерционный", работающий по принципу центробежного насоса. В данном случае обе ЭДСEиE' создают индукционный ток одного направления. При изменении направления вращения диска, ток изменит свое направление.

ЭДС "инерционного" генератора можно определить из следующих соображений. На электрон массы m, находящийся на расстоянии от центра диска, действует центробежная сила инерции

F_ин=-ma=-m²=-4²n²m,

где а – центростремительное ускорение электрона, обусловленное его вращением вместе с диском.

Подставив это значение F_ин(опуская знак "-") в формулу (1), получим

E. (4)

Сравнив величины E,E' по формулам (4) и (2), имеем

E^’/E=

Так как для электрона m/e=5,710^-12кг/Кл, то данное отношение весьма мало, а это означает, что величиной E' можно пренебречь. Однако в случае слабых магнитных полей и больших скоростей вращения диска действие "инерционного" генератора необходимо учитывать.

4.1.5. В цепи, состоящей из параллельно включенных: катушки индуктивности, активное сопротивление которой R₁=5,0 Ом, а L=0,34 Гн; сопротивления R₂=95 Ом; источника с ЭДСE=38 В, имеется ключ К, с помощью которого можно либо включать источник тока, либо его выключать. Внутреннее сопротивление батареи пренебрежимо мало. Определить силу тока в резисторе R₂в трех случаях: 1) до размыкания цепи; 2) в первый момент после размыкания; 3) через 0,01 с после размыкания.

Решение. 1. Силу тока I₂до размыкания цепи найдём по второму правилу Кирхгофа, применив его для контура, состоящего из R₂и батареи сE

I₂R₂+Ir=E,

где I – сила тока в батарее;

r – внутреннее сопротивление источника.

Поскольку внутренним сопротивлением батареи можно пренебречь, получим

I₂R₂=E, I₂=E/R₂=0,40 А.

2. Найдем силу тока I₂' в резисторе R₂сразу же после размыкания ключа К. Если в первом случае резистор R₂и катушка L были соединены между собой параллельно, то после отключения батареи они, образуя один неразветвленный контур, оказываются соединенными последовательно. Следовательно, по ним должен течь одинаковый ток. Так как из двух участков только один обладает индуктивностью, то именно ток I₁, проходивший до размыкания цепи по этому участку, должен сохраниться. Такой результат приобретает простой физический смысл: поскольку индуктивность является мерой инертности тока в проводнике, то ток I₂в резисторе R₂, практически лишенный инертности, сразу исчезнет после отключения батареи и по всему контуру потечет ток I₁. Таким образом, получаем ответ

I₂'=I₁=E/R₁=7,6 А.

3. Так как в данном случае цепь отключена от батареи, ток начнет убывать. Его величину I₂'' в заданный момент времени t=0,01 с можно определить по формуле для изменения тока при замыкании и размыкании

E/R,

где I₀=0 – начальная сила тока при замыкании цепи;

E=0 – при размыкании цепи.

В рассматриваемом случае E=0 (случай размыкания), I₀=I₁.

Следовательно, имеем

I₂''=I₁exp(-Rt/L), (1)

где R=(R₁+R₂) – общее сопротивление цепи.

Подставив числовые значения величин I₁, R₁, R₂, L, t, в формулу (1) и произведя вычисления, найдем:

I₂''=0,4 А.

Ответ: I₂=0,4 А; I₂'=7,6 А; I₂''=0,4 А.

4.1.6. Резистор сопротивлением R присоединен к верхним концам двух вертикальных медных стержней, отстоящих на расстояниидруг от друга. Стержни замкнуты медной перемычкой массы m, которая без трения может скользить по ним. В окружающем пространстве создано однородное магнитное поле с индукцией B, перпендикулярное плоскости, в которой расположены стержни. Перемычку отпустили, после чего она начала падать без нарушения электрического контакта. Пренебрегая сопротивлением стержней и перемычки, найти установившуюся скорость v последней. Принять индуктивность единицы длины системы стержней равной k.

Решение. При падении перемычки площадь контура, образованного резистором, стержнями и перемычкой, растет, и магнитный поток сквозь него увеличивается. Согласно закону Фарадея, в контуре появляется ЭДС электромагнитной индукции, вызывающая индукционный ток. Следовательно, на перемычку кроме силы тяжести mgдействует со стороны магнитного поля сила Ампера F_А, определяемая формулой:

dF_А=I[B].

Так как для всех элементов длины перемычки, по которой идет ток силой I, sina=1 и B=const, то

F_А=IB.

Согласно правилу Ленца, сила F_Анаправлена против силы mg. С ростом скорости падения перемычки увеличивается ЭДС индукции, сила тока I и, следовательно, сила Ампера F_А. Скорость перестанет возрастать, когда наступит равновесие сил mg иFА, т.е.

mg=IB. (1)

Из условия (1) можно найти силу тока I, а последнюю связать с искомой скоростью, применив закон Ома и закон электромагнитной индукции. По закону Ома для замкнутой цепи

I=E/R, (2)

где E=(E_i+E_s) – ЭДС, действующая в контуре;

E_i– ЭДС индукции, возникающая при изменении сквозь контур магнитного потока Ф₁вектора B;

E_s– ЭДС самоиндукции, которая появляется при изменении магнитного потока Фs сквозь контур, созданного индукционным током. Этот поток изменяется вследствие роста площади контура.

Величину E_iможно определить из следующих соображений:

E=(3)

где q – величина заряда.

При движении в магнитном поле проводника ad вместе с ним движутся со скоростью v его свободные заряды (электроны). Поэтому на каждый из них действует сила Лоренца, выполняющая роль сторонней силы F_ст, входящей в формулу (3). Поскольку векторv перпендикулярен векторуB, то силу Лоренца можно определить по формуле

F_л=qvBsin=qvB.

Так как она действует только вдоль участка ad длиной , интеграл, стоящий в (3), равен



Подставив это значение интеграла в формулу (3), получим

E=vB. (4)

Чтобы определить величину E_s, учтем, что в данном случае индуктивность контура величина переменная. Действительно, индуктивность L=kx, где x – длина вертикальных стержней, измеренная на участке, по которому идет ток. При падении перемычки величины x и L возрастают. На основании законов электромагнитной индукции и самоиндукции, для ЭДС самоиндукции запишем

E_s=. (5)

Так как при установившейся скорости падения перемычки I=const, то первое слагаемое в (5) равно нулю и тогда

E_s=. (6)

Величины E_iиE_sимеют в данном случае противоположные знаки, поскольку магнитные потоки Ф_iи Ф_sнаправлены, согласно правилу Ленца, противоположно; при этом оба потока растут по абсолютному значению.

Учитывая это, из уравнений (2) – (4) и (6) найдем:

I=(Bv – Ikv)/R. (7)

Исключив из формул (1) и (7) силу тока I, определим установившуюся скорость перемычки:

. (8)

Проанализируем полученный результат.

1. Если k=0, то v=mgR/B²²и направлена вниз. Так как при наличии индуктивности скорость, будучи величиной конечной, направлена также вниз, то приходим к выводу, что формула (8) верна лишь при значениях заданных величин, удовлетворяющих неравенству

B²²>mgk. (9)

Выясним физический смысл этого соотношения. Из (1) следует, что значение I, необходимое для равновесия приложенных к перемычке сил, равно:

I=mg/B. (10)

Однако индуктивность цепи ограничивает рост силы тока в контуре, происходящий при увеличении скорости перемычки. Действительно, из (7) находим

I=B/(R/v+k).

Отсюда, предположив v, получим предельную силу тока:

I_пред=B/k. (11)

Сопоставляя формулы (9) – (11), видим, что неравенство (9) эквивалентно очевидному условию I_пред>I. Следовательно

1Если соотношение (9) не выполняется, то это означает, что сила тока в контуре, ограниченная в процессе самоиндукции величиной I_пред, не достигает значения, необходимого для равновесия сил mg иF_А, приложенных к перемычке, ни при каких конечных значениях ее скорости. Другими словами, скорость перемычки неограниченно возрастает и ее установившееся значение недостижимо.

2. Если R, то v. В этом случае ток по контуру не идет и перемычка падает под действие силы тяжести с ускорение g.

3. Если R=0 и выполняется условие (9), то v=0: перемычка будет неподвижно висеть в магнитном поле, несмотря на действие силы тяжести. Этот парадоксальный результат можно осуществить, если охладить проводника рассматриваемого контура, помещенного в достаточно сильное магнитное поле, до сверхпроводящего состояния.