3. Циркуляция индукции магнитного поля. Вихревой характермагнитного поля. Закон полного тока

Циркуляцией вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляцией вектора напряженности магнитного поля) называют физическую величину, определяемую соотношением:



Закон полного тока (теорема о циркуляции напряженности магнитного поля) – циркуляция вектора напряженности магнитного поля по замкнутому контуру L равна алгебраической сумме токов, охватываемых контуром:



или



Направление обхода и направление тока должны быть связаны между собой правилом правого винта.

Следствия из закона полного тока:

1) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение

,

сохранив величину, изменит знак;

2) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю:

.

Закон полного тока в интегральной форме для циркуляции вектора индукции:

.

Так как

,



то магнитному полю нельзя приписать какой-либо потенциал, а это означает, что магнитное поле является вихревым, а не потенциальным.

Для произвольных токов и контуров справедлив закон полного тока в дифференциальной форме:

rotB=₀j

Напряженность магнитного поля внутри толстых проводников с током

H=j/(2r).

По всему сечению проводника плотность тока j=I/S=I/R², тогда

H=Ir/(R²).

3.1. Магнитный поток. Магнитные цепи.

Поток магнитной индукции (магнитный поток) через площадку dS – физическая величина численно равная произведению проекции Bна направление положительной нормали nи величины этой площадки dS:

dФ_m=B_ndS=BdScos()

Полный поток магнитной индукции через некоторую поверхность S



Для однородного магнитного поля и плоской площадки S

Ф_m=B_ndS.

Теорема Остроградского-Гаусса для магнитных полей



Индукция магнитного поля B в магнитной цепи, состоящей из стального сердечника с воздушным (вакуумным) зазором

где _c_В– соответственно, длина стального и воздушного участков цепи;

_с,_В– их магнитные проницаемости;

I – ток в обмотке цепи;

N – число витков обмотки.

Закон полного тока



Закон Ома для магнитных цепей S:



где IN=E_м– магнитодвижущая сила;

R_мс=– магнитное сопротивление цепи сердечника;

R_мв=– магнитное сопротивление цепи воздушного зазора;

R_м=R_мс+R_мв– полное сопротивление магнитной цепи.

.

Первое правило Кирхгофа – алгебраическая сумма магнитных потоков в участках цепи сходящихся в узле равна нулю:



Знак Ф_мiопределяется направлением соответствующих линий B. Если линии вектора Bсходятся в узле Ф_мi– положителен, если они выходят из узла – Ф_мi– отрицателен.

Второе правило Кирхгофа – в любом замкнутом магнитном контуре, произвольно выбранном в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитное сопротивление соответствующих участков цепи, равна алгебраической сумме магнитодвижущих сил этого контура:



При последовательном соединении магнитопроводов полное магнитное сопротивление равно сумме магнитных сопротивлений отдельных последовательно соединенных участков: R_м=.

При параллельном соединении обратная величина сопротивления разветвленной части магнитной цепи равна сумме обратных величин магнитных сопротивлений отдельных ветвей:



Работа по перемещению проводника и контура с током в магнитном поле:

dA=IdФ_m

т.е. работа, совершаемая силами Ампера по перемещению в магнитном поле проводника, ток в котором постоянен, равна произведению силы тока на величину магнитного потока через поверхность, которую описывает проводник при своем движении.

Если ток постоянен и проводник прямолинейный

A=IФ_m.

Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, равна произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром:

dA=IdФ_m,

где I – величина тока в контуре;

dФ_m– изменение магнитного потока.

Если перемещаемый контур состоит из N витков, то

dA=,

где =– потокосцепление или полный магнитный поток пронизывающий N витков контура.

3.2. Природа магнитных свойств вещества. Магнетики. Диамагнетизм. Диамагнетики и их свойства. Парамагнетизм. Парамагнетики и их свойства. Ферромагнетизм. Ферромагнетики и их свойства. Граничные условия на поверхности

Диамагнитный эффект – появление индуцированных моментов p_iиJ==, направленных против внешнего магнитного поля (или свойство вещества намагничиваться навстречу направлению действующего на него внешнего магнитного поля). Вещества (среда), которые обладают диамагнетизмом, называют диамагнитными или диамагнетиками.

Примечания:

1) диамагнетизм – свойство, присущее любым веществам, так как он обусловлен действием внешнего магнитного поля на электронные орбиты атомов и молекул;

2) изменение скоростей движения электронов по орбитам сопровождается появлением магнитного поля, направленного против внешнего поля и ослабляющего его (закон Ленца); следовательно, любое вещество противодействует проникновению магнитного поля внутрь его объема;

3) диамагнитный эффект не связан с появлением упорядоченности в расположении электронных орбит, поэтому диамагнитная восприимчивость æ не зависит от температуры;

4) вещество является диамагнетиком, если только его атомы и молекулы не имеют собственного магнитного момента; тогда диамагнитный эффект является единственной реакцией вещества на воздействие внешнего магнитного поля.

Магнитный момент электрона, представляющего собой некоторый эквивалентный круговой ток:

p_m=IS=enpr²=ev_or/2,

где e – заряд электрона;

v_o– его скорость;

r – радиус орбиты.

Магнитным момент электронной орбиты

p_m=(e/2m)mv₀r=(e/2m)p,

где p=mv₀r – момент количества движения электрона на орбите.

Изменение скорости электрона приводит к изменению магнитного момента электронной орбиты на:

,

где m – масса электрона;

B₀– индукция внешнего магнитного поля.

Вектор pнаправлен против вектора индукцииB₀внешнего магнитного поля, следовательно, в векторной форме, для каждой орбиты изменение магнитного момента

При помещении вещества во внешнее магнитное поле каждая единица объема, содержащая N электронных орбит, приобретает индуцированный магнитный момент, равный

æ

где

æ=

диамагнитная восприимчивость вещества.

Прецессия Лармора – синхронное вращательное движение совокупности электронов изолированного атома под действием внешнего магнитного поля, относительно оси проходящей через центр атома параллельно направлению H. Вклад каждого электрона в диамагнитную восприимчивость æ_Дизолированного атома равен:

æ_Д=,

где e – заряд электрона;

m – его масса;

c – скорость света в вакууме;

<r²> – средний квадрат расстояния электрона от ядра атома.

Парамагнетизм, свойство веществ (парамагнетиков), помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент) в направлении, совпадающем с направлением этого поля. Вещества, обладающие таким свойством называют парамагнетиками.

Парамагнетизм характерен для веществ, частицы которых (атомы, молекулы, ионы, атомные ядра) обладают собственным магнитным моментом, но в отсутствии внешнего поля эти моменты ориентированы хаотически, так что в целом J=0. Во внешнем магнитном поле магнитные моменты атомов парамагнетиков ориентируются преимущественно по полю, с ростом которого намагниченность увеличивается по закону:

J=æ_mH,

где æ_m– магнитная восприимчивость 1 см³вещества;

H – напряженность внешнего магнитного поля.

Для парамагнетиков æ 10^-7– 10^-4и всегда положительна.

В слабых полях и при низких температурах удельная магнитная воспри-имчивость парамагнитных веществ обратно пропорциональна температуре (закон Кюри):

æ=,

где æ=æ_m/– удельная (массовая) магнитная восприимчивость;

æ_m– магнитная восприимчивость единицы объема вещества;

r - плотность вещества;

C = n²/3k – постоянная Кюри;

n - число молекул в единице объема;

k - постоянная Больцмана;

T - абсолютная температура.

Статистический расчет дает для магнитного момента единицы массы вещества в слабых магнитных полях при температуре T величину

J'=J/=N²H/3kT,

где k – постоянная Больцмана;

N – число молекул.

В сильных магнитных полях и при низких температурах (когда H/T и тепловое движение не нарушает ориентацию магнитных моментов) J'pN, т.е. к насыщению (все атомные моменты ориентированы одинаково), и закон Кюри не выполняется.

Квантовомеханический расчет приводит к cледующей зависимости удельной магнитной восприимчивости от абсолютной температуры,

где g – множитель Ланде;

m_Б– магнетон Бора;

L – квантовое число полного момента.

Закон Кюри применим к парамагнетизму ядер. При отсутствии значительного взаимодействия между спинами ядер и электронов в атомах ядерная магнитная восприимчивость (на 1 моль)

æ_моль=

где p_{m, эфф}– эффективный магнитный момент ядра;

C_я– ядерная постоянная Кюри;

N – число ядер на моль.

Закон Кюри-Вейса обобщает закон Кюри для веществ, в которых носители магнитных моментов взаимодействуют:

æ=C'/(T – ),

где C' и – константы вещества.

Любая частица, обладающая зарядом e и массой m, имеет магнитный момент (магнетон Бора): _Б=_o=,

где h – постоянная Планка;

c – скорость света в вакууме.

Ядерный магнетон:

~ 5,05110^-24эрг/Гс.

Спиновый магнитный момент

_S=2_Б,

Парамагнитная восприимчивость диэлектриков, согласно классической теории Ланжевена, определяется формулой

æ_L=,

где N – число парамагнитных атомов в 1 моле вещества;

_а– магнитный момент атома.

Квантовая теория парамагнетизма диэлектриков, учитывающая пространственное квантование момента _а, для их магнитной восприимчивости (при m_аH<<kT) приводит к формуле:

æ_L=,

где j – квантовое число, определяющее полный момент импульса атома;

g_L– множитель Ланде.

Парамагнитная восприимчивость одного моля полупроводников æ_п, обусловленная электронами проводимости, в простейшем случае зависит от температуры T экспоненциально

æ=AT^1/2exp(-/kT),

где A – константа вещества;

 – ширина запрещенной зоны полупроводника.

Для металлов (без учета диамагнетизма Ландау и взаимодействия электронов)

æ,

где _o– энергия Ферми;

_э– магнитный момент электрона.

Ядерный парамагнетизм при отсутствии сильно взаимодействия между спинами ядер и электронными оболочками атомов характеризуется величиной

æ_я=,

которая приблизительно в 10⁶раз меньше электронной парамагнитной восприимчивости (_э~10³_я). Магнитные моменты атомов возникают в основном за счет двух факторов:

1) орбитального движения электронов. Полный орбитальный магнитный момент атома является суммой орбитальных магнитных моментов отдельных электронов;

2) наличия у каждого электрона собственного магнитного момента, связанного со спином электрона, т.е. собственным механическим моментом электрона.

Ферромагнетизм – магнитоупорядоченное состояние вещества, при котором все магнитные моменты атомных носителей магнетизма в веществе параллельны и оно обладает самопроизвольной намагниченностью. Вещества, у которых установился ферромагнитный порядок атомных магнитных моментов, называют ферромагнитными или ферромагнетиками.

Магнитная восприимчивость æk ферромагнетиков положительна (æ>>0) и достигает значений 10⁴– 10⁵; их намагниченность (вектор намагничивания) Jи вектор индукции магнитного поля Bсвязаны между собой соотношением

B=(H+J)/

Магнитные и другие свойства ферромагнетиков обладают специфической зависимостью от температуры. Намагниченность насыщения J_sимеет наибольшее значение при T=0 K (J_so) и монотонно уменьшается до нуля при температуре, равной температуре Кюри (T=). Вышеферромагнетик переходит в парамагнитное состояние, а в некоторых случаях (редкоземельные металлы) – в антиферромагнитное. При H=0 переход ферромагнетик – парамагнетик, как правило, является фазовым переходом второго рода.

Обменное взаимодействие, приводящее к ферромагнетизму, учитывается введением эффективного молекулярного поля

H_эфф=AJ_s.

Энергия обменного взаимодействия U квадратично зависит от J_s:

U=-H_эффJ_s=,

где A – постоянная молекулярного поля (A>0);

J_s– намагниченность насыщения.

При низких температурах описание свойств ферромагнетиков возможно только с помощью квантовомеханической теории спиновых волн, согласно которой самопроизвольная намагниченность должна убывать с ростом температуры по закону Блоха: J_s=J_so(1-T^3/2),

где J_so– намагниченность насыщения при T=0.

В отсутствие внешнего магнитного поля ферромагнетик можно представить состоящим из областей однородной намагниченности – доменов. В простейшем случае доменная структура представляет собой чередующиеся слои с взаимно противоположным направлением намагниченности.

Ферромагнетики по величине коэрцетивной силы H_сделятся на магнитно-мягкие и магнитно-жесткие. Первые обладают малой H_си значит магнитной проницаемостью. Вторые имеют большие значения H_cи остаточной намагниченностью J_r.

Ферримагнетик – вещества, в которых при температурах ниже точки Кюри T_cсуществует ферримагнитное упорядочение магнитных ионов.

Ферримагнетизм – магнитоупорядоченное состояние вещества, в котором магнитные моменты атомных носителей магнетизма образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг к другу или имеющими более сложную пространственную ориентацию; отличная от нуля векторная сумма намагниченностей подрешеток определяет самопроизвольную намагниченность вещества J_s. Обычно подрешетки отличаются тем, что содержат ионы иной валентности или ионы другого металла.

Антиферромагнетизм – магнитоупорядоченное состояние вещества, характеризующееся тем, что магнитные моменты соседних частиц вещества – атомных носителей магнетизма ориентированы навстречу друг другу (антипараллельно), и поэтому намагниченность тела в целом в отсутствии магнитного поля равна нулю.

Магнитострикция – изменение формы и размеров ферромагнетиков и ферримагнетиков при их намагничивании.

Обратное по отношению к магнитострикции явление – изменение намагниченности ферромагнитного образца при деформации – называется магнитоупругим эффектом или эффектом Виллари.

Магнитное охлаждение – метод получения температур ниже 1К путем адиабатического размагничивания парамагнитных веществ.

Магнетокалорический эффект – изменение температуры магнетика при адиабатическом изменении напряженности магнитного поля H, в котором находится магнетик.

На границе раздела двух магнетиков нормальные составляющие вектора Bнепрерывны

B_1n=B_2n.

Если на границе раздела двух сред ток проводимости отсутствует, то

H_2t=H_1t,

т.е. тангенциальные составляющие вектора Hна границе раздела двух магнетиков непрерывны.

Закон преломления силовых линий векторов B иHпри переходе через границу раздела двух магнетиков



Первое начало термодинамики для магнетика Q=dU+A,

где Q – количество сообщенного тепла;

dU – приращение внутренней энергии;

A – работа магнетика, которая складывается из работы A'= pdV против внешнего давления и работы магнитного поля



Если предположить, что намагничивание магнетика либо не сопровождается заметными изменениями его объема, либо этот объем поддерживается постоянным, то работа магнетика будет равна работе магнитного поля, которую можно отнести к единице объема магнетика, тогда

A=A"=(-H dB)/4,

Q=dU – (H dB)/4.

Основные уравнения термодинамики магнетиков для: свободной энергии

F=U – TS,

dF=-SdT+(H dB)/4.

термодинамического потенциала Ф=F – HB/4.

dФ=-SdT – (B dH)/4.

энтальпии I=U – HB/4.

dI=TdS – (B dH)/4.

изменения внутренней энергии

dU=TdS+(H dB)/4.

Выражение для внутренней энергии магнетика U:



Изменение температуры магнетика в зависимости от изменения напряжен-ности магнитного поля:

,

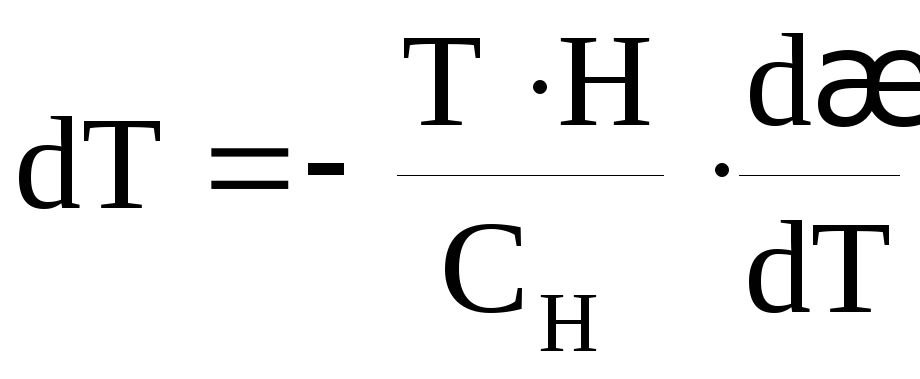или

где C_H– теплоемкость единицы объема магнетика при постоянной напряженности магнитного поля.

Изменение температуры парамагнетика

.

или



Для парамагнитного газа, к которому применима классическая теория теплоемкостей, под C_Hследует понимать молярную теплоемкость при постоянном объеме C_v=iR/2,

где i – число степеней свободы;

R – универсальная газовая постоянная.

Молярная теплоемкость ферромагнетика при постоянном магнитном поле

C_H=ip/(2T),

