2. Принцип суперпозиции магнитного поля. Закон Био-Савара–Лапласа
Индукция магнитного полясозданного объёмным элементом тока(закон Био-Савара-Лапласа):
Для линейного элемента тока:
Результирующая индукция магнитного поля для замкнутых постоянных токов
Напряженность магнитного поля, порождаемого бесконечно длинным проводником с током I, в точке М равноудаленной от его концов
При симметричном расположении точки М относительно концов проводника cos1=– cos2, тогда
,
где I – сила тока в проводнике;
r – расстояние от элемента проводника dl до рассматриваемой точки поля;
1,2– углы между направлением тока в проводнике и направлением на рассматриваемую точку поля;
– численное значение вектора, равного
элементу проводника, направление
которого совпадает с направлением тока.
Для бесконечно длинного проводника 0,, тогда
.
Индукция магнитного поля бесконечного прямолинейного проводника с током:
.
Магнитное поле на оси кругового проводника, радиусом R, в котором существует ток I, является результирующим полем от всех элементов проводника и его напряжённость
Численное значение
где R – радиус кругового проводника;
r – расстояние от элемента проводника dдо рассматриваемой точки поля.
Так как =2R;
r=
,
то
где r0– расстояние от центра до рассматриваемой точки поля на оси кругового проводника.
При r0=0, т.е. в центре кругового проводника
H=I/2R.
Соленоид – катушка цилиндрической формы из проволоки, витки которой намотаны в одном направлении и прилегают плотно друг к другу.
Напряженность магнитного поля внутри соленоида, длина которого – , радиус витка – R, число витков – N, сила тока – I магнитного поля в точке А:
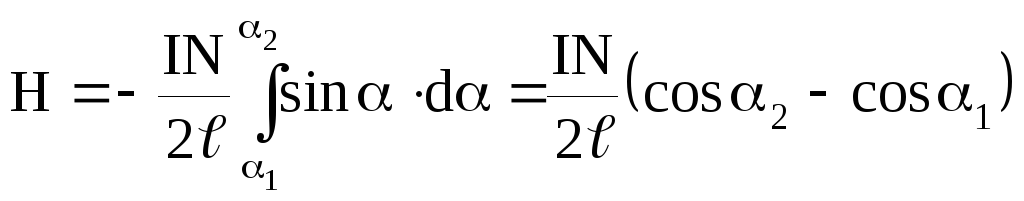
У бесконечно длинного соленоида 20 и11800.
В этом случае:
H=IN/=In,
где n=N/– число витков на единице длины соленоида.
– длина участка;
I – величина тока в соленоиде.
У соленоида конечной длины сказываться так называемый краевой эффект. Поэтому напряженность его магнитного поля равна
H=nI/2.
Магнитное поле тороида (тороид – соленоид свитый в кольцо) однородно и замкнуто внутри самого тороида; вне тороида поле отсутствует
Напряжённость поля тороида
H=IN/=In=IN/2r, или H=nIR/r,
где =2r – длина оси тороида;
r – радиус тороидального кольца;
I – сила тока;
N – число витков тороида:
n – число витков на единицу длины тороида.
2.1. Примеры решения задач.
2.1.1. По отрезку прямого провода длиной=80 см течет ток I= 50 А. Определить магнитную индукцию Bполя, создаваемого этим током, в точке А равноудаленной от концов отрезка провода и находящейся на расстоянии r0=30 см от его середины.
Решение.Для решения задачи воспользуемся законом Био-Савара-Лапласа и принципом суперпозиции магнитных полей. Закон Био-Савара-Лапласа позволяет определить магнитную индукцию dB, создаваемую элементом тока Id. Заметим, что направление вектора dBв рассматриваемой точке А определяется правилом правого винта. Принцип суперпозиции магнитных полей позволяет для определения Bвоспользоваться геометрическим суммированием (интегрированием):
, (1)
где символ означает, что интегрирование распространяется на всю длину провода.
Запишем закон Био-Савара-Лапласа в векторной форме:
,
где dB– магнитная индукция, создаваемая элементом провода длиной dl с током I в точке, определяемой радиус-вектором r;
0– магнитная постоянная;
– магнитная проницаемость среды, в которой находится провод. В нашем случае =1.
Примечание. Во всех задачах, где это специально не оговорено, следует считать, что средой является воздух, для которого магнитная проницаемость принимается равной единице.
Заметим, что векторы dBот различных элементов тока сонаправлены, поэтому выражение (1) можно переписать в скалярной форме:
где
В скалярном выражении закона Био-Савара-Лапласа угол – угол между элементом тока Idlи радиусом-вектором r. Таким образом,
. (2)
Преобразуем подынтегральное выражение так, чтобы была одна переменная – угол . Для этого выразим длину элемента провода dчерез угол d: d==rd/sin. Тогда подынтегральное выражение sind/r2запишем в виде sinrd/(r2sin)=d/r. Заметим, что переменная r также зависит от, (r==r0/sin); следовательно, d/r=sind/r0.
Таким образом, выражение (2) можно переписать в виде
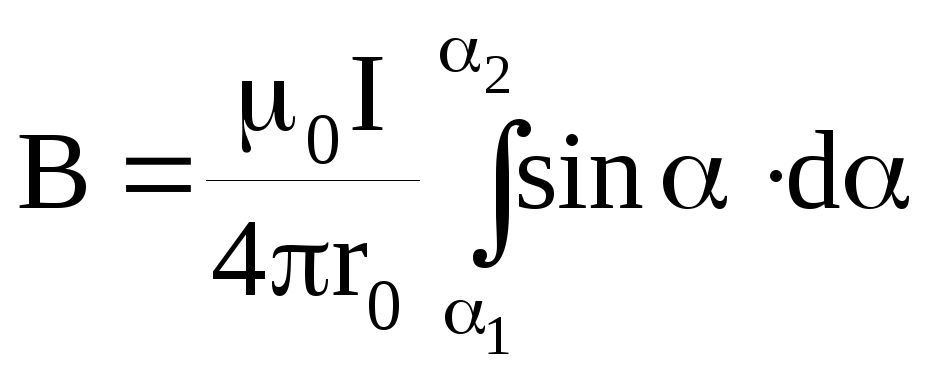
где 1, a2– пределы интегрирования – углы между направлением тока в проводнике и направлениями на рассматриваемую точку.
Выполним интегрирование:
. (3)
Заметим, что при симметричном расположении точки А относительно отрезка провода cos2=-cos1. С учетом этого формула (3) примет вид
. (4)
Определив cos1=
,
подставив его значение в (4), получим
. (5)
Произведя вычисление по формуле (5), найдем B=26,710-6Тл.
Направление вектора магнитной индукции Bполя, создаваемого прямым током, можно определить по правилу правого винта. Для этого необходимо провести магнитную силовую линии и по касательной к ней в интересующей нас точке проводим вектор B. Вектор магнитной индукцииBнаправлен перпендикулярно плоскости.
Ответ: B=26,710-6Тл=26,7 мкТл.
2.1.2.По тонкому проводящему кольцу радиусом R=10 см течет ток I=80 А. Найти магнитную индукцию Bв точке А, равноудаленной от всех точек кольца на расстоянии r=20 см.
Решение. Для решения задачи воспользуемся законом Био-Савара-Лапласа:
,
где dB– магнитная индукция, создаваемая элементом провода длиной dl с током I в точке, определяемой радиус-вектором r.
Выделим на кольце элемент dи от него в точку А проведем радиус-вектор r. Вектор dBнаправим в соответствии с правилом правого винта. Согласно принципу суперпозиции магнитных полей, магнитная индукцияBв точке А определяется интегрированием:
,
где интегрирование производится по всем элементам кольца d.
Разложим вектор dBна две составляющие dB1, перпендикулярную плоскости кольца, и dB2, параллельную плоскости кольца, т.е.
dB=dB1dB2.
Тогда
Заметив, что
из соображений симметрии и что векторы
различных
элементов dl сонаправлены, заменим
векторное суммирование (интегрирование)
скалярным:
где dB1=dBcosи dB=0Id/(4r2) (поскольку dперпендикулярен r и, следовательно, sina=1);
– угол между плоскостью кольца и направлением на рассматриваемую точку А.
Таким образом,
.
После сокращения на 2и замены cosна R/r получим
.
Выразим все величины в единицах СИ и произведем вычисления:
Тл.
Ответ: B=6,310-5Тл.