1. Магнитное поле и его характеристики. Магнитное поле и магнитный момент кругового тока. Магнитное взаимодействие токов. Силы Ампера и Лоренца

Магнитостатика – раздел теории электромагнитного поля, в котором изучаются свойства стационарного магнитного поля (полей постоянных электрических токов или поля постоянных магнитов)а также движение заряженных частиц в стационарном магнитном поле.

Теорема эквивалентности поля магнитных зарядов и поля постоянных электрических токов (теорема Ампера)“Магнитное поле предельно тонкого плоского магнита ("магнитного листка", образованного из одинаково ориентированных элементарных магнитиков) тождественно полю замкнутого (кругового) линейного тока, текущего по контуру этого магнита”.

Пробный ток (пробный контур) – ток существующий в плоском замкнутом контуре малых размеров (круговой ток). Положение этого контура в пространстве определяется с помощью положительной нормали, связанной с током в контуре правилом правого винта. Свойства контура характеризуются векторной физической величиной – магнитным моментом p_m, численно равным:

p_m=IS,

где I – величина тока в контуре;

S – площадь охватываемая контуром.

Вращающий момент, действующий на пробный контур, пропорционален его магнитному моменту, синусу угла между направлением положительной нормали и направлением магнитного поля в данном месте пространства:

M_вр~p_msin=ISsin.

Вращающий момент M_врсвязан с индукцией магнитного поляBсоотношением

M_вр=p_mBsin,

В векторной форме

M_вр=[p_mB].

Индукция магнитного поля характеризует силовое воздействие магнитного поля на ток (движущиеся электрические заряды

Индукция магнитного поля – векторная физическая величина, численно равная вращающему моменту, действующему на пробный контур, помещенный перпендикулярно к направлению магнитного поля в данную точку, магнитный момент которого равен единице:

,

при p_m=1 и sina=1: B=M_вр.

Различают: 1. Макротоки – упорядоченное движение электрических зарядов в объеме проводника;

2. Микротоки – обусловлены наличием в атомах вещества вращающихся вокруг ядер с большой скоростью (10¹⁵с^-1) электронов. Движение каждого электрона эквивалентно замкнутому контуру с током.

В пространстве может существовать результирующее магнитное поле макро – и микротоков. Индукция магнитного поля B(магнитная индукция) является характеристикой этого результирующего поля макро – и микротоков. Поэтому, при прочих равных условиях и одном и том же макротоке в проводнике, величинаBв различных средах различна.

Напряженность магнитного поля H– характеристика магнитных полей, порождаемых только макротоками. Связь напряженности магнитного поля H с магнитной индукциейB:

B=₀H,

где ₀– магнитная постоянная ;

 – относительная магнитная проницаемость среды, которая показывает во сколько раз магнитное поле макротоков усиливается за счет магнитных полей микротоков.

Напряженность магнитного поля не зависит от свойств среды. Орбитальный магнитный момент микротока вещества:

p_m=IS,

где I – величина эквивалентного тока (микротока);

S – площадь орбиты электрона.

Вектор намагничения J– характеристика магнитных полей микротоков вещества – магнитный момент единицы объема:

где V – физически бесконечно малый объёмвзятый в окрестности рассматриваемой точкиp_m – магнитный момент отдельной молекулыСуммирование производится по всем молекуламзаключённым в объёмеV

В вакууме микротоки (молекулярные токи) отсутствуют и вектор намагничения: J_вак=0.

В отсутствии внешнего магнитного поля магнетик обычно не намагничен:

J=0 приH=0.

В магнетиках во внешнем магнитном поле(и не слишком сильных полях), кроме так называемых ферромагнетиков, зависимостьJотHявляется практически линейной:

J=_mH,

где _m– магнитная восприимчивость вещества, характеризующая его магнитные свойства.

Между векторами B, Hи Jсуществует связь:

B/₀=H+J.

или

B=₀(1+_m)H=₀H,

где =(1+_m) – относительная магнитная проницаемость среды.

Магнитное поле нескольких токов характеризуется результирующими векторами B илиH, которые определяются согласно принципу суперпозиции магнитных полей:

B=B₁+B₂+....+B_n=

H=H₁+H₂+....+H_n =

Сила F_m, действующая на движущийся точечный заряд q в магнитном поле

F_m=

где – B– индукция магнитного поля;

v– скорость движения заряда;

q – величина заряда;

c – некоторая постоянная, зависящая от выбора системы единиц измерения физических величин.

В электрическом поле Eна заряд q действует сила

F_e=qE.

При совместном действии на движущийся электрический заряд q электрического и магнитного полей возникает сила Лоренца:

F_л=F_e+ F_m=q(E+[vB]).

Сила действующая в магнитном поле на элемент объема тела dV:

dF =e [vB]dN=ne[vB]dV,

или dF=[jB]dV,

где e – величина заряда электрона

n – концентрация свободных электронов

dN=ndV – число заряженных частиц в объеме dV;

j=nev– плотность тока;

v– скорость направленного движения свободных электронов;

B– индукция магнитного поля.

Сила Ампера (закон Ампера)

dF=[dlB].

Сила, действующая на провод конечной длины:

,

где длина проводника.

Величина силы, действующей со стороны однородного магнитного поля на прямолинейный проводник с током

F=IBsin.

В случае неоднородного поля и проводника произвольной формы

dF=IBdlsin.

Направление силы Ампера определяется по правилу левой руки.

1. Примеры решения задач

1.1.1.Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи силой I=60 А, расположены на расстоянии d=10 см друг от друга. Определить индукцию магнитного поля B, создаваемого проводниками в точке А, отстоящей от оси одного проводника на расстоянии r₁=5 см, от другого – r₂=12 см. Проводники и рассматриваемая точка поля не находятся на одной прямой

Решение. Для определения индукции магнитного поля Bв рассматриваемой точке А воспользуемся принципом суперпозиции магнитных полей. Сначала определим направления магнитных индукций B₁ иB₂полей, создаваемых каждым проводником с током в отдельности. Индукция результирующего магнитного поля равна геометрической сумме:

B=B₁+B₂.

Модуль вектора Bв этом случае может быть найден по теореме косинусов:

, (1)

где – угол между векторами B₁ иB₂.

Магнитные индукции B₁ иB₂выражаются соответственно через силу тока I и расстояний r₁, r₂от проводников до точки А

, 

где =1 – относительная магнитная проницаемость воздуха.

Подставляя выражения B₁и B₂в формулу (1) и вынося из под корня, получим:

 (2)

Вычислим cosзная расстояния d, r₁, r₂, по теореме косинусов:

,

где d – расстояние между проводами.

Отсюда

Размерность полученного результата очевидна.

Подставим в формулу (2) числовые значения физических величин и произведем вычисление

Ответ: B=3,110^-4Тл.

1.1.2.Длинный провод с током I=50 А изогнут под углом=2/3. Определить магнитную индукцию Bв точке А, расположенной от углана продолжении оси одного из концов провода. Расстояние от угла до рассматриваемой точки поля d=5 см.

Решение.Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в некоторой точке О. В соответствии с принципом суперпозиции магнитных полей магнитная индукция Bв точке А равна геометрической сумме магнитных индукций B₁ иB₂ полей, создаваемых отрезками длинных проводов 1 и 2, т.е.B=B₁+B₂. Магнитная индукцияB₂=0, так как точка А лежит на оси провода 2.

Магнитную индукцию B₁ найдем, воспользовавшись соотношением:



где =1 – относительная магнитная проницаемость среды (воздуха);

₁и₂– углы между направлением тока в проводнике и направлением на рассматриваемую точку поля;

r_o– кратчайшее расстояние от провода 1 до точки А.

В нашем случае ₁0 (провод длинный),₂==2/3 (cos₂=cos(2/3)=-1/2). Расстояние r_o=d sin(–)=d sin(/3). Тогда магнитная индукция



Произведем вычисления:



Ответ: B₁=3,510^-5Тл.

1.1.3.Два бесконечно длинных провода скрещены под прямым углом. По проводам текут токи I₁=80 А и I₂=60 А. Расстояние между проводами d=10 см. Определить магнитную индукцию Bв точке А расположенной между проводами, удаленной от них на одинаковом расстоянии r=d/2.

Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукцияBполя, создаваемого токами I₁и I₂, определяется выражением:

B=B₁+B₂,

где B₁,B₂– соответственно магнитные индукции полей, создаваемых этими токами в рассматриваемой точке.

Заметим, что векторы B₁ иB₂взаимно перпендикулярны. Тогда модуль вектораBможно определить по теореме Пифагора:



где B₁ и B₂определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного проводника с током:



В нашем случае r_o=d/2. Тогда



Произведем вычисления:

.

Ответ: B=410^-4Тл.

1.1.4.Бесконечно длинный провод изогнут так, что в его середине образовалась полуокружность с радиусом R=10 см. Образовавшиеся концы провода взаимно перпендикулярны. Определить индукцию магнитного поля B (магнитную индукциюB) в точке О (в центре полуокружности) током I=80 А, текущим по этому проводу.

Решение.Магнитную индукцию Bв точке О найдем, используя принцип суперпозиции магнитных полей:



В нашем случае провод разбить на три части: два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда

B=B₁+B₂+B₃,

где B₁,B₂,B₃– магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.

Так как точка О лежит на оси первого участка провода, то

B₁=0

и тогда

B=B₂+B₃.

Учитывая, что векторы B₂иB₃направлены в соответствии с правилом правого винта (правилом векторного умножения) перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим

B=B₂+B₃.

Магнитную индукцию B₂найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:

.

Так как магнитное поле в точке О создается лишь половиной такого кругового тока и в воздухе (среда не определена), то

.

Магнитную индукцию B₃определим, воспользовавшись соотношением для бесконечно длинного проводника с током:

.

В данном случае r_o=R,₁=/2 (cos₁=0),₂(cos₂=-1). Тогда



Используя найденные выражения для B₃и B₃, получим



Произведем вычисления:

.

Ответ: B=3,3110^-4Тл.

1.1.5.По двум параллельным прямым проводам длиной=2,5 м каждый, находящимся на расстоянии d=20 см друг от друга, текут одинаковые токи I=1 кА, в одном направлении. Вычислить силу взаимодействия токов.

Решение. Взаимодействие двух проводов, по которым текут токи, осуществляется благодаря наличию вокруг них магнитных полей. Каждый из проводов создает собственное магнитное поле, которое действует на другой провод.

Оба тока I₁и I₂текут в одном направлении. Предположим, что первый ток создает магнитное поле, а второй помещается в него. Так как>>d, то провода можно считать бесконечно длинными. Тогда модуль индукции магнитного поля первого тока определяется соотношением

(1)

(считаем, что провода находятся в воздухе).

Согласно закону Ампера, на каждый элемент второго провода с током I₂длиной dl действует в магнитном поле сила

dF=I₂B₁dlsin,

где – угол между направлением вектора dlи направлением вектора B₁.

Векторы dlиB₁взаимно перпендикулярны, следовательно sin= 1, а

dF=I₂B₁dl.

Подставив в это выражение значение B₁согласно (1), получим

.

Силу взаимодействия проводов с током найдем интегрированием:



Заметив, что I₁=I₂₌I, получим



Произведем вычисления:



Ответ: F=2,5 Н.

1.1.6.По проводнику, согнутому в виде квадратной рамки со стороной 10 см, течет ток силой 5 А. Определить напряженность магнитного поля в точке, расположенной на перпендикуляре к его центру и равноудаленной от вершин квадрата на расстояние, равное его стороне.

Решение. Искомая напряженность Hмагнитного поля в точке А является векторной суммой напряженностей H₁, H₂, H₃, H₄, создаваемых в этой точке токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата. Из соображений симметрии все четыре напряженности по абсолютной величине равны между собой. Геометрическая сумма H=H₁++H₂+H₃+H₄будет направлена вдоль оси 001 (перпендикуляра к плоскости квадрата) и равна сумме проекций всех векторов на направление этой оси, т.е. H=4H₁, или

H=4H₁cos,

где – угол между вектором H₁и осью 001.

Если построить чертеж, то можно убедиться, что

,

тогда

(1)

Напряженность магнитного поля, создаваемого отрезком провода, выражается формулой:

 (2)

где I – сила тока в проводнике;

r – кратчайшее расстояние от проводника до точки, напряженность поля в которой надо определить;

₁,₂– углы, образованные направлением тока в проводнике и радиусами-векторами, проведенными от концов проводника к точке А.

В данном случае ₂=–₁, следовательно, cos₂=– cos₁, и выражение (2) приобретает вид:

(3)

Подставляя это выражение H₁в формулу (1):

 (4)

Заметив, что

и cos₂₌0,5

равенство (4) перепишем в виде:



Произведем вычисления:

А/м.

Ответ: H=11 А/м.

1.1.7.Квадратная рамка со стороной 2 см, содержащая 100 витков тонкого провода подвешена на упругой нити, постоянная кручения которой 0,1 гсм/град. Плоскость рамки совпадает с направлением линий напряженности внешнего магнитного поля. Определить напряженность внешнего магнитного поля, если при пропускании по рамке тока силой 1 А она повернулась на угол 60^o.

Решение. Напряженность внешнего магнитного поля H может быть найдена из условия равновесия рамки в поле.

Рамка будет находиться в равновесии в том случае, если сумма вращающих моментов, действующих на нее, будет равна нулю:

. (1)

В данном случае на рамку действуют два момента: M₁ – момент сил, с которым внешнее магнитное поле действует на рамку с током, иM₂– момент упругих сил, возникающих при закручивании нити, на которой она подвешена. Следовательно, формула (1) может быть переписана в виде:

M₁+M₂=0.

Так как M₁=p_mBsin; M₂=-C, то

p_mBsin-C=0, (2)

где p_m– магнитный момент рамки с током;

B – индукция магнитного поля;

 – угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля;

 – угол, на который повернется рамка;

С – постоянная кручения, показывающая величину момента упругой силы, возникающей при повороте рамки на угол, равный единице.

Знак "минус" в выражении для M₂ставится потому, что этот момент противоположен по направлению моменту M₁сил, действующих на рамку со стороны магнитного поля.

Если учесть, что p_m=ISN=Ia²N, B=_oH,

где I – сила тока в рамке;

S - площадь рамки;

a - сторона квадратной рамки;

N - число витков рамки;

_o- магнитная постоянная;

H – напряженность магнитного поля,

то равенство (2) можно переписать в виде:

_oIa²NHsina – C=0,

откуда

 (3)

Так как =/2 –, значит sin=cos, то равенство (3) примет вид:

 (4)

Подставив значения величин, входящих в (4) в системе СИ, будем иметь:



Ответ: H=2,310⁴А/м.

1.1.8.Плоский квадратный контур со стороной а=10 см, по которому течет ток I=100 А, свободно установился в однородном магнитном поле индукцией B==1 Тл. Определить работу, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1)₁=90^o; 2)₂=3^o. При повороте контура сила тока в нем поддерживается постоянной.

Решение. Как известно, на контур с током в магнитном поле действует вращающий момент

M=p_mBsin, (1)

где p_m– магнитный момент контура;

B – индукция магнитного поля;

 -угол между векторами p_m иB.

По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (M=0), а значит, =0, т.е. вектора p_mиBсовпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение.

Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный ( зависит от угла поворота ), то для подсчета работы применим формулу работы в дифференциальной форме:

dA=Md.

Подставив сюда выражение M по (1) и учтя, что

p_m=IS=Ia²,

где I – сила тока в контуре;

S=a²– площадь контура,

Получим

dA=Md=p_mBsind=Ia²Bsind. (2)

Проинтегрировав (2), найдем работу при повороте контура на конечный угол:

 (3)

1) Работа при повороте на угол ₁=90^o:

. (4)

Выразив числовые значения величин в единицах системы СИ, подставив в (4), будем иметь: A₁=1001(0,1)²=1 Дж.

2) Работа при повороте на угол ₂=3^o.

В этом случае, учитывая, что угол ₂мал, заменим в выражении (3) sin:

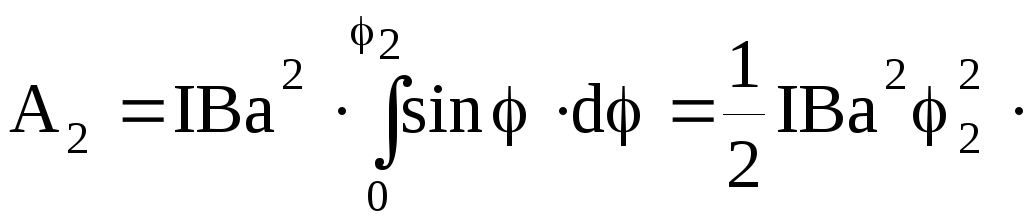(5)

Выразим угол ₂в радианах. После подстановки числовых значений величин в (5), найдем:

A₂=0,51001(0,1)²(0,0523)²=1,410^-3Дж.

Ответ: A₁=1 Дж; A₂=1,410^-3Дж.

1.1.9.Коаксиальный кабель представляет собой длинную металлическую тонкостенную трубку радиуса R=10 мм, вдоль оси которой расположен тонкий провод. Силы токов в трубке и проводе равны, направления противоположны. Определить магнитную индукцию в точках 1 и 2, удаленных соответственно на расстояния r₁=5 мм и r₂=15 мм от оси кабеля, если сила тока I=0,50 А.

Решение. Магнитная индукция в каждой из точек 1 и 2 равна векторной сумме магнитных индукций, созданных двумя токами: трубки и осевого провода. Индукция магнитного поля осевого провода можно определить по формуле

B₁=_oI/(2d), (1)

где d – расстояние от точки А до оси проводника.

Мысленно выделив на трубке тонкие полоски, параллельные осевому проводу, можно представить ток трубки как совокупность параллельных токов, идущих по эти полоскам. Индукция магнитного поля каждого такого тока можно определить по формуле

dB=_odI/(2d). (2)

Индукция магнитного поля тока трубки будет определяться суммированием (интегрированием) магнитных индукций dBэлементарных прямолинейных проводников с током. Однако этот метод неудобен, так как хотя магнитное поле тока, текущего по коаксиальному кабелю, является осесимметричным (его ось симметрии совпадает с осью кабеля), точки 1 и 2 не лежат на этой оси. Поэтому при суммировании векторов dB, имеющих различное направление, нельзя воспользоваться соображениями симметрии.

Симметрия магнитного поля тока коаксиального кабеля позволяет решить задачу, применив теорему о циркуляции вектора индукции магнитного поля. Действительно из соображений симметрии следует, что линии индукции магнитного поля тока кабеля, являясь замкнутыми, должны иметь форму окружностей, центры которых лежат на оси кабеля и плоскости которых перпендикулярны этой оси. При этомиз тех же соображений симметрии вытекает, что во всех точках одной и той же линии индукции величина B одинакова. В этом случае целесообразно применить формулу



В качестве контура интегрирования рассмотрим линию индукции магнитного поля, проходящую через точку 1. Учитывая, что для всех элементов этой линии cos(B,dl)=1, запишем



откуда



Выразив в единицах СИ входящие в формулу величины, произведя вычисления, получим:



Аналогично определим величину B₂. Для этого в качестве контура интегрирования возьмем линию индукции, проходящую через точку 2. Поскольку контур интегрирования охватывает два тока, равных по модулю и противоположно направленных, то

откуда B₂=0.

Замечание. Полученные результаты позволяют сделать следующие выводы:

1. Магнитное поле тока, идущего по коаксиальному кабелю, сосредоточено целиком внутри кабеля.

2. Это поле таково, как если бы его создавал один ток, идущий по осевому проводу. Следовательно, ток, идущий по трубе кабеля (тонкостенному длинному цилиндру), не создает внутри нее магнитного поля.

3. Отсутствие результирующего поля вне кабеля свидетельствует о численном равенстве (и противоположном направлении) магнитных индукций токов трубки и осевого провода. Другими словами, магнитное поле тока, идущего по длинному цилиндра, для точек, вне цилиндра, можно рассчитывать, заменив цилиндр линейным проводником, расположенным вдоль оси цилиндра.

1.1.10.Длинный цилиндр из диэлектрика, по поверхности которого равномерно распределен положительный заряд с линейной плотностью=10 мкКл/м, вращается вокруг своей оси, совершая n_o=100 об/с. Определить индукцию магнитного поля в двух точках: в середине оси цилиндра и в центре одного из его оснований.

Решение.Прежде всего заметим, что круговое движение электрических зарядов при вращении длинного цилиндра соответствует току, проходящему по виткам соленоида, имеющего такие же размеры, что и цилиндр. Следовательно, магнитное поле данного вращающегося цилиндра эквивалентно магнитному полю длинного соленоида с током. Поэтому индукцию магнитного поля в середине цилиндра вычислим по формуле:

 (1)

Чтобы выразить произведение nI через заданные в условии величины n_oи, рассмотрим прямоугольную площадкуS, сторона которой, параллельна оси цилиндра, имеет единичную длину. За каждый оборот цилиндра через эту площадку проходит весь заряд, расположенный на поверхности цилиндра единичной длины, т.е. заряд, численно равный величине. Следовательно, через площадкуS за промежуток времениt пройдет заряд, численно равный

q'=n_ot. (2)

В случае соленоида через такую же площадку S за промежуток времениt пройдет заряд, численно равный

q''=nIt(3)

Магнитные поля токов соленоида и вращающегося цилиндра эквивалентны при условии q'=q''. Приравнивая правые части формул (2), (3), получаем nI=n_o.

Подставив это значение nI в формулу (1), найдем индукцию магнитного поля в середине вращающегося цилиндра:

B_А=_on_o. (4)

Чтобы определить индукцию магнитного поля в центре одного из оснований цилиндра, учтем, что в задаче речь идет о бесконечно длинном цилиндре, длина которого значительно превышает его диаметр. Если мысленно разделить цилиндр пополам плоскостью, перпендикулярной оси вращения, и удалить одну половину, то индукция магнитного поля в точке А уменьшится вдвое и станет равной

B_А'=_on_o/2.

Это вытекает из принципа суперпозиции магнитных полей, в силу которого каждая половина вращающегося цилиндра вносила одинаковый вклад в магнитное поле в точке А. В тоже время индукция в точке, расположенной в центре одного из оснований цилиндра, не изменится при удалении одной из половин цилиндра, так как при большой длине оставшейся половины цилиндра вклад, вносимый в магнитное поле этой точки удаленной половины, был пренебрежимо мал. Но из соображений симметрии следует, что магнитные поля у концов оставшейся половины должны быть одинаковыми. Таким образом, получаем

B_C=B_А'=_on_o/2. (5)

Подставив числовые значения величин, выраженные в единицах системы СИ, в формулы (4) и (5), произведем вычисление:

B_А=410^-71001,0010^-5=12,610^-10Тл.

B_С=(410^-71001,0010^-5)/2=6,310^-10Тл.

Ответ: B_А=12,610^-10ТлB_С=6,310^-10Тл.

1.1.11.В центре длинного соленоида, имеющего n=5000 витков на метр, помещена рамка, состоящая из N=50 витков провода площадью S= 4,0 см²каждый. Рамка может вращаться вокруг оси ОО', перпендикулярной оси соленоида, и удерживаться в равновесии спиральной пружиной так, что при этом ее плоскость параллельна оси соленоида. При пропускании тока по рамке и соленоиду, соединенных последовательно, рамка повернулась на угол=60^o. Определить силу тока, если жесткость пружины k=6,0010^-5Нм/рад. (Жесткость спиральной пружины измеряется вращающим моментом, необходимым для закручивания пружины на угол=1 радиану).

Решение. При появлении тока рамка оказывается в однородном поле соленоида. На нее будет действовать вращающий момент M, под действием которого рамка повернется, закручивая пружину. Рамка установится в таком положении, когда вращающий момент магнитных силMуравновесится моментом упругих силM_упр.пружины, т.е.

M=-M_упр. (1)

Момент Mнайдем по формуле:

M=p_mBsin, (2)

где p_m=IS – магнитный момент одного витка рамки;

B=_onI – индукция магнитного поля соленоида.

С учетом того, что рамка состоит из N витков, формулу (2) перепишем в виде:

M=NIS_onIsin=_onI²NSsin, (3)

где – угол между векторами p_m и B. Заметим, что в отсутствии тока=/2.

При устойчивом равновесии свободной рамки вектор p_mвсегда параллелен вектору Bи при этом=0. Поэтому под действием момента магнитных сил M рамка поворачивается так, что уголуменьшается. Если рамка повернулась на угол, то возникающий при этом момент упругих сил M_упр. пружины согласно закону Гука равен:

M_упр=k, (4)

где k – жесткость пружины.

Приравняв на основании (1) правые части формул (3), (4) и учитывая, что =2 –, получим:

_onI²NScos=k,

откуда I=[(k)/(_onNScos)]^1/2.

Выразив все величины в единицах системы СИ, произведем вычисления:

I=[(6,0010^-5/3)/(410^-750510³4,010^-40,50)]^1/2=1,0 А.

Ответ: I=1,0 А.

1.1.12.Рядом с длинным прямым проводом MN, по которому идет ток силой I, расположена квадратная рамка со стороной, с током I'. Рамка лежит в одной плоскости с проводом MN так, что одна ее сторона, ближайшая к проводу, находится на расстоянии a_o. Определить магнитную силу, действующую на рамку, а также работу этой силы при удалении рамки из магнитного поля. Считать, что при движении рамки токи I и I' поддерживаются постоянными.

Решение. В данном случае рамка с током находится в неоднородном магнитном поле, так как магнитная индукция Bубывает при удалении от провода MN. В этом случае на контур кроме вращающего момента действует сила. Перемещая контур, эта сила совершает работу.

На каждый элемент длины контура рамки, расположенного в магнитном поле тока I, действует сила Ампера:

dF=I[dl B].

Направление этой силы зависит, в частности, от направления вектора магнитной индукции Bв том месте, где находится этот элемент. Направления линий индукции, определяются правилом правого винта. Применив правило левой руки, найдем направления сил, действующих на все стороны рамки. Так как две стороны рамки перпендикулярны проводу MN, расположены одинаково относительно провода, то действующие на них силы численно равны, но противоположны по направлению (F₃=F₄), уравновешивают друг друга. Следовательно, равнодействующая всех сил, приложенных к рамке, численно равна разности сил, действующих на стороны рамки, расположенный параллельно проводу MN и направлена в сторону от провода:

F=F₁– F₂, (1)

где F₁, F₂– соответственно силы, действующие на ближнюю и удаленную от провода стороны рамки.

Силы F₁и F₂можно определить, воспользовавшись законом Ампера:

dF_А=I'dlBsin(dl,B). (2)

Учтем, что для всех элементов dl одной и той же стороны рамки sin(dl,B)=1 и величина B одинакова. Поэтому силу, действующую на каждую из сторон, на основании (2) выразим так:

. (3)

Магнитная индукция длинного прямого провода с током определяется формулой

. (4)

Подставив это значение B в (3), найдем:

, (5)

где a – расстояние от соответствующей стороны рамки до провода MN.

В рассматриваемом случае:

; .

Тогда результирующая сила F, будет равна:

 (6)

При удалении рамки от провода за пределы магнитного поля тока I силы F₁, F₂, которые теперь будем рассматривать как переменные величины, совершат работу: сила F₁– положительную A₁, сила F₂– отрицательную работу A₂. Считая каждую из величин A₁, A₂работой переменной силы, найдем полную работу, совершенную магнитными силами:

. (7)

Чтобы вычислить каждый из этих интегралов, надо знать, как зависит сила от расстояния до провода MN. Формула (5) определяет эту зависимость, однако она верна лишь для бесконечно длинного провода. При значительном удалении от провода условия ₁=0 и₂=перестают выполняться и формула (5) перестает быть верной. Однако, найти разность интегралов, стоящую в формуле (7), можно. Для этого воспользуемся тем, что сила F₁, переместив ближайшую к проводу сторону квадрата на расстояние, в дальнейшем совершит точно такую же по абсолютному значению работу, что и сила F₂, перемещающая противоположную сторону квадрата, так как первый проводник, пройдя путь, затем в точности повторит движение второго проводника. Имея противоположные знаки, эти два значения работы дают в сумме нуль. Следовательно, искомая работа равна работе силы F₁при перемещения первого проводника из начального положения на расстояние. Поэтому, учитывая формулу (5), получим



1.1.13.Рядом с длинным прямым проводом MN, по которому идет ток силой I, расположена квадратная рамка со стороной, с током I'. Рамка лежит в одной плоскости с воду, находится на расстоянии a_o. Определить магнитную проводом MN так, что одна ее сторона, ближайшая к просилу, действующую на рамку, а также работу этой силы при удалении рамки из магнитного поля. Считать, что при движении рамки токи I и I' поддерживаются постоянными.

Решение.Для вычисления работы по удалению рамки из магнитного поля воспользуемся формулой, выражающей работу магнитных сил через изменение магнитного потокаA=IФ,

где Ф=Ф – Ф_o– изменение магнитного потока;

Ф_o– магнитный потокпронизывающий рамку в ее начальном положении;

Ф – магнитный потокпронизывающий рамку, находящуюся вне магнитного поля (Ф=0).

Таким образом, работа сил магнитного поля:

A=I'Ф=I'(Ф – Ф_o)=-I'Ф_o. (1)

Найдем поток Ф_oпо формуле

 (2)

где B_n– проекция вектора Bна направление положительной нормали к элементу площади dS.

Так как положительное направление нормали к контуру с током связано с направлением тока правилом правого винта, то для всех элементов dS поверхности, ограниченной контуром, вектор Bсоставляет угол, то B_n=– B, поток Ф_o, определяемый формулой (2), является отрицательным, а работа А, выражаемая формулой (1), – положительной.

Чтобы вычислить величину Ф_o, разобьем поверхность, ограниченную контуром рамки, на элементарные полоски, параллельные проводу MN, длинойи шириной da. Магнитный поток сквозь такую полоску, расположенную от провода MN на расстоянии а, равен:

Ф₀=B_ndS=-Bda.

Так как ,

то



Тогда поток через весь контур рамки

 (3)

Подставив это значение Ф_oв формулу (1), получим



Для определения силы, действующей на рамку, предположим, что рамка под действием этой силы переместилась из своего начального положения, причем её расстояние от провода возросло на малую величину a. При этом сила F совершит работуА=Fa.

C другой стороны, эту работу можно выразить через изменение магнитного потока Ф сквозь рамку при ее перемещении наа:

А=I'Ф.

Из последних двух равенств, переходя к пределу, получаем

F=I'(dФ/dа). (4)

Чтобы выполнить дифференцирование, выразим Ф как функцию переменной величины а – расстояние от провода MN до второй стороны , параллельной проводу

.

Подставим это значение Ф (4) и произведем дифференцирование:



Замечания:1. Этот метод более удобен по сравнению с ранее рассмотренным, поскольку он позволяет не учитывать силы, действующие на отдельные элементы контура. Как видно из формулы (4), достаточно вычислить производную от магнитного потока по перемещению контура в каком-либо направлении, чтобы определить силу, действующую в этом направлении на контур.

2. При удалении рамки от провода MN магнитный поток сквозь нее возрастал, поскольку начальный поток Ф_o<0, и, согласно (1), силы поля, перемещая рамку, совершали положительную работу. Однако магнитные силы выталкивают рамку с током из поля провода MN лишь до тех пор, пока сохраняется первоначальная ориентация рамки относительно провода. Если же представить, что рамка повернулась вокруг оси ОО', проходящей через середину его сторон параллельно проводу MN, на небольшой угол, то силы F₁, F₂уже не будут лежать на одной прямой. Они создадут вращающий момент, в результате чего рамка повернется на угол p (при этом магнитный поток сквозь рамку станет положительным). Таким образом, рамка, удерживаемая осью ОО', будет находиться в неустойчивом равновесии. Поэтому в действительности рамка, если она свободна, сначала повернется относительно данной оси на угол p, а затем начнет притягиваться к проводу MN. Последнее легко понять, если определить направление сил, которые теперь будут действовать на стороны рамки, перпендикулярные проводу. Это следует также из формулы (1): теперь магнитный поток сквозь рамку положителен. Следовательно, он возрастает (dФ>0) при приближении рамки к проводу (da<0). Значит, производная dФ/dа, а с ней и сила F – величины отрицательные, что соответствует притяжению рамки к проводу MN.

Во всех случаях рамка с током перемещается под действием силы F так, что при этом магнитный поток сквозь нее возрастает.