Предварительные сведения

_{Уравнение Максвелла в дифференциальной форме имеет вид:}

_{I пара или}

IIпара или

К уравнениям добавляют связи:

,

где

,

.

Под уравнением волны понимают уравнение вида , где- смещение точки с координатамиx,y,zв момент времениt.

Волна, у которой фронт волны и волновая поверхность являются плоскостями, называется плоской волной.

Её уравнение , где координатная осьXнаправлена по направлению распространения волны, то есть перпендикулярно волновым поверхностям.

Пусть при x= 0:

.

Тогда в произвольном значении xколебания придут с запозданием:

Зафиксировав фазуи продифференцировав- получим скорость, с которой перемещается данное значение фазы – фазовая скорость.

Учитывая, что ,, уравнение волны примет вид:

где - волновое число.

Затухание плоской волны, как показа опыт, происходит по экспоненциальному закону

Для точечного источника амплитуда убывает с расстоянием ~1/rдаже в непоглощенной среде

где r– расстояние от точечного источника.

Для волны (плоской) распространяющейся в направлении под углами к осям x, y, zуравнение волны примет вид:

где - волновой вектор

Учитывая, что , уравнение плоской волны можно записать:

где - комплексное число, называемое комплексной амплитудой,.

Уравнение любой волны является решением дифференцированного уравнения, называемого волновым.

Если продифференцировать функцию дважды поx, y, z, t, сложить производные по координатам и учесть, что, получим уравнение, которое называют волновым

- волновое уравнение

Всякая функция, удовлетворяющая уравнению этого вида, описывает некоторую волну. Корень квадратный из величины, обратной коэффициенту придает фазовую скорость этой волны.

Световая волна. Основные характеристики световой волны

Развитие физики показало, что свет – сложное явление (волна, частица). Мы изучаем волновую оптику, которая описывает световые явления с точки зрения волновой природы света. Свет – это электромагнитная волна, то есть система вихревых электрических и магнитных полей взаимно порождающих друг друга.

Существование электромагнитных волн вытекает из уравнений Максвелла:

- оператор Гамильтона (2)

В случае однородной нейтральной и непроводимой среды j=0 и постояннымии:

Тогда уравнения (2) запишутся:

Взяв операцию ротор от первых двух уравнений, поменяв последовательность дифференцирования по координатам и по времени, с учетом оставшихся уравнений, получим уравнения:

(3)

Учтено, что .

Это и есть волновые уравнения, которое неразрывно связаны друг с другом, описывают некоторую волну, скорость которой (фазовая):

(3’)

В вакууме == 1,=с.

Рассматривая плоскую электромагнитную волну, распространяющуюся по направлению осиX(тогда компонентыне будут зависеть отyиz) и записывая уравнения Максвелла, получим, что векторыперпендикулярны, а волновые уравнения примут вид:

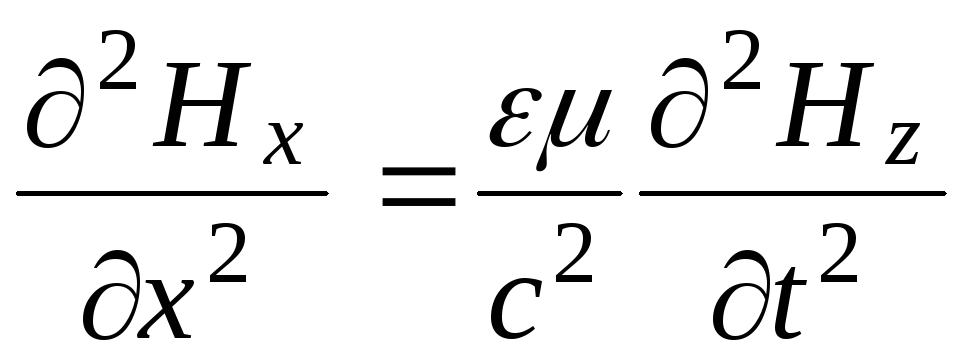
Векторы направлены вдоль взаимно перпендикулярных осейXиY.

Решением последних уравнений являются функции:

(4)

Для того, чтобы эти решения удовлетворяли уравнениям Максвелла, необходимо равенство начальных фаз₁ и₂и

(5)

Таким образом, колебания электрических и магнитных векторов в электромагнитных волнах происходят в одной фазе (₁ =₂), а амплитуды связаны соотношением

.

Моментальный снимок электромагнитных волн: векторы образуют правовинтовую систему с направлением распространения волны. В фиксированной точке пространства векторыизменяются по гармоничному закону. Уравнения (4) можно записать с учетом сказанного в векторном виде:

Лекция №2