4.4. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний

Вынужденными колебаниями называются такие, которые совершаются системами под действием внешней (вынуждающей) силы, изменяющейся по какому-либо закону, например гармоническому.

Рис.4.6

Рассмотрим колебательную систему – груз, присоединённый к пружине (рис.4.6). Пусть на груз действует гармоническая сила

. (4.36)

Эта сила называется вынуждающей. Частота её изменения – , амплитуда –. С учетом вынуждающей силы можем записать

или

. (4.37)

Применяя полученные ранее значения  и ₀, получим

. (4.38)

Рассмотрим уравнение (4.38) в простом случае, когда :

. (4.39)

Естественно предположить, что с течением времени тело будет совершать гармонические колебания с частотой вынуждающей силы , т.е.

. (4.40)

Причём , т.к.. После подстановки (4.40) в (4.39) получим

. (4.41)

Откуда имеем

. (4.42)

Рис.4.7

При амплитуда вынужденных колебаний стремится к бесконечности. Однако в действительности амплитуда возрастает, но остаётся конечной, т.к. существует диссипация энергии. На рис.4.7 показана зависимость амплитуды вынужденных колебанийот частоты изменения вынуждающей силы.

Решая дифференциальное уравнение (4.38), учитывающее затухание, можно получить следующую зависимость и  = f():

; (4.43)

. (4.44)

Именно зависимость представлена на рис.4.7 графически.

Исследование функции на экстремум можно осуществить, исследуя на экстремум подкоренное выражение в формуле (4.43). Для чего приравняем производную к нулю:

.

. (4.45)

Частота вынуждающей силы, при которой амплитуда колебаний системы достигает максимума, называется резонансной . Из (4.45) получаем

. (4.46)

Таким образом, можно записать

. (4.47)

При совпадении частоты изменения вынуждающей силы с частотой резонансных колебаний системы амплитуда колебаний достигнет максимальных значений. Подставляя в формулу (4.43) выражение резонансной частоты, находим максимальное значение амплитуды колебаний

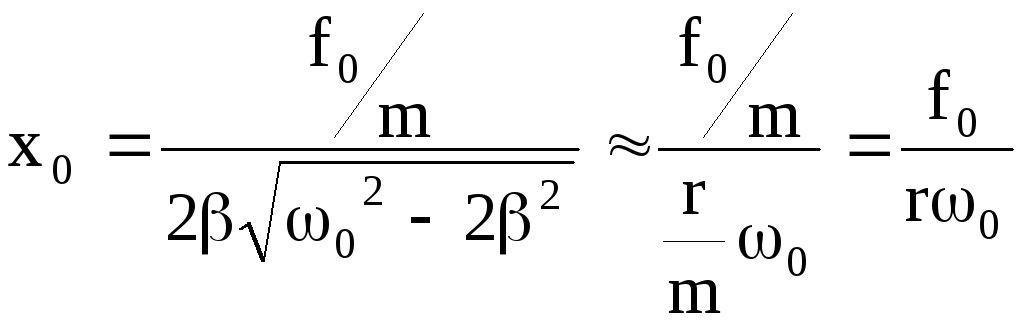. (4.48)

Амплитуда резонансных колебаний тем больше, чем меньше коэффициент затухания и чем больше амплитуда вынуждающей силы.

Представляют интерес два предельных случая: случай очень низких частот и случай очень высоких частотизменения вынуждающей силы. Переходя к соответствующему пределу в формуле (4.43), мы получим:

а) на низких частотах , т.е. выполняется закон Гука;

б) на высоких частотах , , т.е. в результате преобладания сил инерции смещение тела из положения равновесия убывает.

Более строгая теория колебаний утверждает, что уравнение вынужденных колебаний (4.38) является дифференциальным, неоднородным, второго порядка, решением которого является выражение вида:

x = x₁ + x₂ = x₀e^-tsin(ω't + φ₀') + x₀sin(ωt + φ), (4.49)

где ;

x₁ = x₀e^-tsin(ω't + φ₀') – решение однородного уравнения;

x₂ = x₀sin(ωt + φ).

И только тогда, когда колебания системы будут установившимися (t), решение уравнения (4.38) можно описать только вторым слагаемым

x₂ = x₀sin(ωt + φ). (4.50)

Из формулы (4.43) вытекает, что при малом затухании (т.е. при βω₀) амплитуда при резонансе приближенно равна

. (4.51)

Разделим (4.51) на смещение x от положения равновесия под действием постоянной силы f₀, равное f₀/m₀². В результате получим

. (4.52)

Таким образом, добротность показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы от положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо только при небольшом затухании).

С явлением резонанса приходится считаться при конструировании машин и сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае могут возникнуть вибрации, которые могут вызвать катастрофу.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т.д.

Методы возбуждения вынужденных колебаний различны: путем непосредственного воздействия на колебательную систему (раскачка маятника периодическими толчками) - чаще всего называемые вынужденными; путем периодического изменения параметров колебательной системы (длины подвеса маятника) - так называемое параметрическое возбуждение колебаний; либо благодаря развитию неустойчивостей и возникновению самосогласованных колебательных движений внутри самой системы - так называемые автоколебания.

Особое значение при возбуждении колебаний имеет явление резонанса, заключающееся в резком увеличении амплитуды колебаний при приближении частоты внешнего воздействия к некоторой резонансной частоте, характеризующей систему. Если последняя линейна и параметры ее не зависят от времени, то резонансные частоты совпадают с частотами ее собственных колебаний, и соответствующий отклик тем сильнее, чем выше добротность. Раскачка происходит до тех пор, пока энергия, вносимая извне (например, при каждом отклонении маятника), превышает потери за период осцилляций. Для линейных колебаний энергия, получаемая от источника, пропорциональна первой степени амплитуды, а потери растут пропорционально ее квадрату, поэтому баланс энергий всегда достижим.

При больших амплитудах колебания становятся нелинейными, происходит смещение собственной частоты системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды колебаний может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении колебаний в системах с распределенными параметрами максимум амплитуды достигается в случае пространственно-временного резонанса. В этом случае не только частота внешнего воздействия, но и его распределение по координатам, хорошо "подогнаны" к структуре нормальной моды или, на языке бегущих волн, когда наступает совмещение не только их частот (резонанс), но и волновых векторов (синхронизм).

Существует некоторый выделенный класс вынужденных колебаний, в котором внешнее воздействие, не являясь чисто колебательным (например, мгновенный удар), имеет, однако, настолько богатый частотный спектр, что в нем всегда содержатся резонансные частоты системы. Например, заряженная частица, пролетающая между двумя металлическими плоскостями, возбуждает почти весь набор нормальных электромагнитных колебаний и волн, свойственный этой системе. К этому можно отнести черенковское излучение или тормозное излучение частицы в однородных средах, когда и спектр внешних воздействий, и спектр собственных колебаний - оба сплошные, т.е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных колебаний в системах с непрерывным спектром собственных частот типа ротатора (маховик, колесо, электромагнитное поле и т.п.), где вращательное движение ( а следовательно, и два ортогональных колебательных движения) может возбуждаться силами, неизменными во времени.

Параметрическое возбуждение колебаний возникает при периодическом воздействии на те параметры системы, которые определяют величину запасенной колебательной энергии: у маятника - это длина нити или масса груза (но не коэффициент трения); в электрическом контуре - это индуктивность и емкость (но не сопротивление).

При определенных условиях в такой нелинейной колебательной системе могут возникать непрекращающиеся самоподдерживающиеся колебания, или автоколебания, при которых внешнему источнику отводится лишь функция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть начальное состояние системы неустойчиво либо по отношению к ничтожно малым флуктуациям (мягкий режим возбуждения), либо по отношению к определенным конечным возмущениям (жесткий режим возбуждения). В любом случае спонтанно (случайно) возникшее колебание начнет увеличиваться по амплитуде (процесс усиления колебания), эти усиленные колебания через элемент положительной обратной связи, обеспечивающий самосогласованность фаз, снова "подаются" в место своего возникновения и снова усиливаются и т.д. Получается очень быстрый (чаще всего экспоненциальный) рост колебаний. Ограничение колебаний наступает из-за рассогласованности фаз, а также из-за конечности энергетических ресурсов.

Лекция 5. Ангармонические колебания

Нелинейный осциллятор. Физические системы, содержащие нелинейность. Автоколебания. Условие самовозбуждения колебаний. Роль нелинейности. Предельные циклы.