Лекция 5. Постоянный электрический ток

Постоянный электрический ток. Основные действия и условия существования постоянного тока. Основные характеристики постоянного электрического тока: величина /сила/ тока, плотность тока. Сторонние силы. Электродвижущая сила, напряжение и разность потенциалов. Их физический смысл. Связь между ЭДС, напряжением и разностью потенциалов.

5.1. Постоянный электрический ток. Основные действия и условия существования постоянного тока

Электрическим током называют всякое упорядоченное движение электрических зарядов.

Электрический ток, возникающий в проводниках под влиянием электрического поля и представляющий собой частично упорядоченное движение электронов или ионов относительно проводника под влиянием электрического поля, называют током проводимости.

Ток проводимости может существовать как в проводниках первого рода (металлах, графите, некоторых электронных полупроводниках и т.д.), так и в проводниках второго рода (электролитах, расплавах солей, щелочей и т. д.).

О наличии тока в проводниках судят по его действиям на окружающую среду. Основными действиями электрического тока являются:

а) возникновение вокруг проводников с током магнитного поля;

б) выделение в проводниках тепла;

в) биологическое.

Так как перемещение электрических зарядов происходит под действием электрического поля, то одним из основных условий существования тока проводимости в проводниках является наличие в них электрического поля. Следовательно, для увеличения времени существования электрического тока проводимости в проводниках необходимо поддерживать в них существование электрического поля, что возможно при создании на концах проводников разности потенциалов.

Надо отметить, что электрический ток можно получить, если перемещать в пространстве какие-либо заряженные тела. Такой ток называют конвекционным.

5.2. Основные характеристики постоянного электрического тока: величина /сила/ тока, плотность тока. Сторонние силы

Скалярная физическая величина, которая показывает, какой заряд переносится носителями через рассматриваемую поверхность (например, через поперечное сечение проводника) в единицу времени, называется величиной (силой) тока:

. (5.1)

В системе СИ сила тока измеряется в амперах (А). Ампер - это сила такого электрического тока, который, проходя по двум прямолинейным бесконечным проводникам, расположенным на расстоянии 1 м друг от друга, вызывает на каждом участке длиной 1 м силу взаимодействия 210^-7 Н.

Векторная физическая величина, численно равная силе тока через площадку dS, перпендикулярную направлению движения электрических зарядов (электрического тока), называется плотностью тока:

. (5.2)

Плотность тока – векторная величина. За направление вектора плотности электрического тока j принимается направление вектора скорости упорядоченного движения положительных зарядов.

Зная вектор плотности тока j в любой точке проводника, можно определить величину тока через любую поверхность:

, (5.3)

где j_n = jcos – проекция вектора плотности тока на направление тока;

 – угол между векторами j и n (положительной нормали к площадке dS).

Таким образом, сила тока через какую-либо поверхность является потоком вектора плотности тока через поверхность.

Если имеется некоторый объем проводника V, ограниченный поверхностью S, то выражение определяет заряд, выходящий из объема V в единицу времени. При этом скорость убывания заряда, находящегося в данном объеме (на основании закона сохранения заряда),

, (5.4)

где .

Подставляя значение заряда в формулу (5.4) получим

или

. (5.5)

Преобразуем левую часть выражения (5.5) по теореме Остроградского-Гаусса ():

. (5.6)

Следовательно, имеем

.

Откуда

. (5.7)

Соотношение (5.7) является уравнением непрерывности для вектора плотности электрического тока. Оно выражает закон сохранения электрических зарядов.

Уравнение непрерывности вектора плотности электрического тока позволяет ввести (по аналогии с линиями вектора напряженности электрического поля E) линии вектора плотности электрического тока. Так как для стационарного (постоянного) тока

, (5.8)

то можно утверждать, что линии вектора плотности электрического тока всегда замкнуты (рис. 5.1).

При наличии тока в проводнике j 0 и, следовательно, E  0. Таким образом, внутри проводника с током имеется электрическое поле (в электростатике поле внутри проводника нет). Кроме того, плотность постоянного тока по сечению проводника распределена неравномерно.

Вблизи поверхности проводника плотность тока может быть направлена только по касательной к поверхности проводника. Это означает, что и напряженность электрического поля E вблизи поверхности проводника направлена по касательной к его поверхности. Что касается эквипотенциальных поверхностей, то они перпендикулярны поверхности проводника. При этом эквипотенциальные поверхности изогнутых проводников не могут находиться на неизменном расстоянии друг от друга во всех точках проводника. Например, в кольцевом проводнике круглого сечения расстояние между эквипотенциальными поверхностями на внутренней части кольца меньше, чем на внешней. Так как расстояние между соседними эквипотенциальными поверхностями изменяется, то изменяется и напряженность электрического поля в соответствующих точках эквипотенциальных поверхностей. А это и означает, что плотность тока в однородных проводниках изменяется по сечению.

Надо отметить, что в круговом проводнике цилиндрической формы бесконечной длины (в линейном проводнике) эквипотенциальные поверхности внутри проводника представляют собой плоскости, перпендикулярные оси проводника. Поэтому по сечению такого проводника плотность электрического тока и напряженность электрического поля постоянны.

Т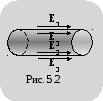аким образом, вблизи поверхности вне проводника имеется электрическое поле, тангенциальная составляющая вектора напряженности E_ которого равна тангенциальной составляющей вектора напряженности электрического поля внутри проводника (рис. 5.2).

В однородных проводниках первого рода источником электрического поля являются поверхностные заряды. Поверхностная плотность этих зарядов

, (5.9)

где E_n – нормальная составляющая вектора напряженности электрического поля вблизи его поверхности.

Вобщем случае силовые линии электрического поля – не касательные к поверхности проводника. Это означает, что наряду с тангенциальной составляющей вектора напряженности электрического поля вблизи поверхности проводника имеется также нормальная составляющая вектораE (рис. 5.3). При этом внутри проводника E_n = 0. Поверхностная плотность электрических зарядов на различных участках проводника может быть как положительной, так и отрицательной.

В неоднородных проводниках проводимость проводников может изменяться от точки к точке в объеме проводника. В стационарном случае , а, где объемная плотность зарядов, равная сумме объемной плотности свободных зарядов₁ и объемной плотности связанных зарядов _св,

.

Тогда

, (5.10)

где  – удельная проводимость проводника.

Учитывая выражение , имеем

. (5.11)

Направляя ось X вдоль прямолинейного участка проводника и считая, что его свойства изменяются только в этом направлении, формулу (5.11) можно переписать в виде

. (5.12)

Если проводимость проводника уменьшается в направлении тока проводимости, то объемная плотность заряда положительна. Это связано с тем, что при постоянной площади сечения проводника плотность тока должна быть постоянной, поэтому для поддержания постоянства тока необходимо увеличивать напряженность электрического поля. Увеличение напряженности электрического поля обеспечивается объемными положительными зарядами.

Аналогично можно объяснить возникновение отрицательных объемных зарядов при увеличении проводимости проводника в направлении тока.

Ток, не изменяющийся по величине и направлению с течением времени, называют постоянным.

Для постоянного электрического тока

; . (5.13)

Существование постоянного тока в проводниках возможно при наличии сторонних сил, которые не могут иметь электростатическое происхождение. Это связано с тем, что электростатическое поле является потенциальным. Следовательно, работа, совершаемая электростатическими силами по замкнутому контуру, в котором существует ток, равна нулю, т. е. при этих условиях существование электрического тока в проводнике невозможно, так как он должен совершать работу по преодолению электрического сопротивления проводника. Существование тока в проводниках доказывает, что сторонние силы имеют не электростатическое происхождение.

Сторонние силы могут быть любой природы, например механической или электрической (сила, действующая на заряд в электрическом поле, возникающем по закону электромагнитной индукции).

Схема простейшего источника тока, в котором сторонняя сила (сторонняя ЭДС) имеет механическое происхождение, представлена на рисунке 5.4.

Между электродами А и В имеется нейтральна среда с равным числом положительных и отрицательных зарядов. Сторонняя сила неэлектростатического происхождения перемещает положительные заряды к электроду В, а отрицательные – к электроду А. В результате этого электрод А заряжается отрицательно, а электрод В - положительно. Во внешней цепи от В к А течет электрический ток, совершающий соответствующую работу. Необходимая для этого энергия сообщается системе сторонними силами, которые совершают работу по разделению электрических зарядов между электродами А и В и доставку этих зарядов на электроды против сил электрического поля с напряженностью E, существующего между электродами. Ток между электродами А и В внутри источника замыкает ток во внешней цепи. Если направление тока рассматривать относительно электродов, то во внешней цепи ток течет от положительного электрода к отрицательному электроду, а внутри источника – от отрицательного электрода к положительному.

Таким образом, сторонние силы разделяют электрические заряды в источниках тока, действуют против кулоновских сил, связывающих разноименные заряды, и характеризуются той работой, которую способны совершить против сил электрического поля внутри источника и против механических сил сопротивления в источнике:

, (5.14)

где A_ст – работа сторонних сил;

A_ис – работа сторонних сил против механических сил сопротивления;

A^' – работа сторонних сил против кулоновских сил.

Выражение (5.14) отображает закон сохранения энергии для источника тока. Работа сторонних сил A_ис равна работе, совершаемой электрическими силами вне источника. Следовательно, источник тока является источником той энергии, которая выделяется во внешнем (по отношению к источнику) участке цепи, тем самым создает разность потенциалов на концах проводника. Для поддержания постоянной разности потенциалов в источнике тока должна непрерывно совершаться работа A_ис, которая компенсирует потерю энергии во внешней цепи.