
- •Оглавление
- •Электромагнитные явления 12
- •От авторов
- •Введение
- •Электромагнитные явления
- •1.1. Магнитное поле в вакууме и его характеристики. Магнитное поле и магнитный момент кругового тока
- •1.2. Закон Био-Савара-Лапласа
- •1.3. Применение закона Био-Савара-Лапласа к расчету магнитных полей прямолинейного и кругового токов
- •1.4. Магнитное взаимодействие токов. Силы Лоренца и Ампера
- •2.1. Циркуляция индукции магнитного поля. Вихревой характер магнитного поля. Теорема о циркуляции индукции магнитного поля (закон полного тока для магнитного поля)
- •2.2. Применение закона полного тока для расчета магнитных полей
- •2.3. Магнитный поток. Магнитные цепи
- •2.4. Работа по перемещению проводника и контура с током в магнитном поле
- •3.1. Природа магнитных свойств вещества. Магнитные моменты атомов. Микро- и макротоки (молекулярные токи)
- •3.2. Магнитное поле в веществе. Намагниченность
- •3.3. Диамагнетизм. Диамагнетики и их свойства
- •3.4. Парамагнетизм. Парамагнетики и их свойства
- •3.5. Элементы теории ферромагнетизма. Ферромагнетики и их свойства
- •3.6. Антиферромагнетизм. Антиферромагнетики и их свойства
- •3.7. Граничные условия на поверхности раздела двух магнетиков
- •4.1. Явление электромагнитной индукции. Основной закон электромагнитной индукции. Правило (закон) Ленца
- •4.2. Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергии
- •4.3. Явление самоиндукции. Магнитное поле бесконечно длинного соленоида. Коэффициенты индуктивности и взаимной индуктивности
- •4.4. Явление самоиндукции при замыкании и размыкании электрической цепи
- •4.5. Энергия магнитного поля. Объемная плотность энергии магнитного поля
- •5.1. Движение заряженных частиц в однородном электрическом поле
- •5.2. Движение заряженных частиц в однородном магнитном поле
- •5.3. Движение заряженных частиц в электрических и магнитных полях. Гальваномагнитные явления
- •5.4. Применение электронных пучков в науке и технике. Понятие об электронной оптике
- •5.5. Эффект Холла
- •6.1. Нелинейный осциллятор. Физические системы, содержащие нелинейность
- •6.2. Получение электромагнитных колебаний. Собственные электромагнитные колебания. Дифференциальное уравнение собственных электромагнитных колебаний и его решение
- •6.3. Затухающие электромагнитные колебания. Дифференциальное уравнение затухающих электромагнитных колебаний и его решение. Характеристики затухающих электромагнитных колебаний
- •6.4. Вынужденные электромагнитные колебания. Дифференциальное уравнение вынужденных электромагнитных колебаний и его решение. Резонанс
- •7.1. Основные положения теории Максвелла
- •7.2. Представление эдс индукции с помощью теоремы Стокса
- •7.3. Представление циркуляции с помощью теоремы Стокса
- •7.4. Ток смещения
- •7.5. Система уравнений Максвелла
- •7.6. Электромагнитные волны. Волновое уравнение. Основные свойства, получение и распространение электромагнитных волн. Энергия электромагнитной (световой) волны. Вектор Умова-Пойтинга
- •7.7. Источники электромагнитного излучения
- •8.1. Релятивистское преобразование электромагнитных полей, зарядов и токов
- •8.2. Инвариантность уравнений Максвелла относительно преобразований Лоренца
- •9.1. Квазистационарное электромагнитное поле
- •9.2. Квазистационарные электрические токи
- •Заключение
- •Рекомендательный список литературы Основной
- •Дополнительный
- •Редактор с.П. Тарасова Компьютерная верстка и макет
6.3. Затухающие электромагнитные колебания. Дифференциальное уравнение затухающих электромагнитных колебаний и его решение. Характеристики затухающих электромагнитных колебаний
При рассмотрении электрических колебаний в простом закрытом колебательном контуре предполагалось, что активное сопротивление R (сопротивление проводников) равно нулю.
Т ак
как любой проводник обладает определенным
сопротивлением R, то колебания в реальном
колебательном контуре с течением времени
затухают. Это связано с выделением
энергии на активном сопротивлении R, в
результате чего энергия контура
уменьшается.
ак
как любой проводник обладает определенным
сопротивлением R, то колебания в реальном
колебательном контуре с течением времени
затухают. Это связано с выделением
энергии на активном сопротивлении R, в
результате чего энергия контура
уменьшается.
На основании второго закона Кирхгофа для контура, содержащего активное сопротивление R, индуктивность L и емкость C (рис. 6.3), можно записать
![]() ,
(6.18)
,
(6.18)
где
![]() .
.
Следовательно,
![]() . (6.19)
. (6.19)
Уравнение (6.19) является уравнением затухающих электромагнитных колебаний. С точки зрения математики, оно однородное, дифференциальное, второго порядка, решением которого является выражение вида
![]() , (6.20)
, (6.20)
где
![]() - амплитуда колебаний;
- амплитуда колебаний;
- коэффициент затухания;
знак «минус» показывает, что с течением времени амплитуда колебаний уменьшается.
Н а
рис. 6.4 представлены затухающие колебания,
подчиняющиеся уравнению (6.20).
а
рис. 6.4 представлены затухающие колебания,
подчиняющиеся уравнению (6.20).
Введя новую
переменную
![]() ;
;![]() ,
определив первую производную
,
определив первую производную![]() и вторую производную
и вторую производную![]() ,
подставив их в формулу (6.20), будем иметь
,
подставив их в формулу (6.20), будем иметь
![]() ,
(6.21)
,
(6.21)
где
![]() - условная циклическая частота.
- условная циклическая частота.
Имеем
![]() . (6.22)
. (6.22)
Из формулы (6.22) действительно следует, что при >0 решением этого уравнения является выражение вида
![]() .
(6.23)
.
(6.23)
Таким образом, условная циклическая частота равна
![]() . (6.24)
. (6.24)
Условный период
![]() . (6.25)
. (6.25)
Названия «условная
циклическая частота» и «условный период»
обусловлены тем, что затухающие
электромагнитные колебания не являются
строго периодическими, так как изменяющаяся
функция
![]() не принимает через равные промежутки
времени одинаковые значения.
не принимает через равные промежутки
времени одинаковые значения.
Период собственных
электромагнитных колебаний
![]() меньше условного периода затухающих
колебаний T, т.е. наличие активного
сопротивления R замедляет колебания.
меньше условного периода затухающих
колебаний T, т.е. наличие активного
сопротивления R замедляет колебания.
Характеристиками затухающих электромагнитных колебаний являются: декремент и логарифмический декремент колебаний.
Декрементом затухания называют отношение двух последовательных значений q, отличающихся по времени на период:
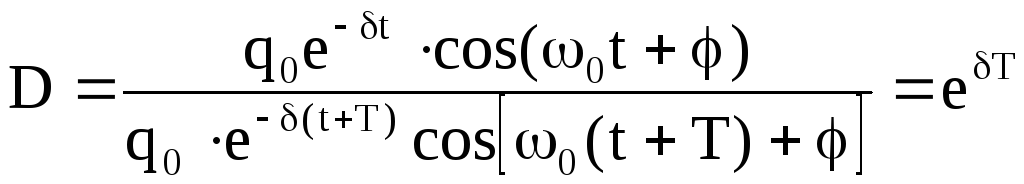 .
(6.26)
.
(6.26)
Логарифмический декремент численно равен натуральному логарифму от декремента затухания:
![]() .
(6.27)
.
(6.27)
Если коэффициент затухания характеризует затухание колебаний за единицу времени, то логарифмический декремент затухания характеризует затухание колебаний за период.
Анализ выражения
для условного периода колебаний
![]() показывает, что при R0,
o2>>2;
TTo.
При R
T имеет смысл при условии (o2
- 2)>0.
Если (o2
- 2)
= 0, то T.
В этом случае колебания быстро затухают.
Такие колебания называют апериодическими.
Можно показать, что условием возникновения
апериодических колебаний является
выражение
показывает, что при R0,
o2>>2;
TTo.
При R
T имеет смысл при условии (o2
- 2)>0.
Если (o2
- 2)
= 0, то T.
В этом случае колебания быстро затухают.
Такие колебания называют апериодическими.
Можно показать, что условием возникновения
апериодических колебаний является
выражение
![]() .
(6.28)
.
(6.28)
Одной из характеристик колебательного контура является его добротность Q:
![]() .
(6.29)
.
(6.29)
где
![]() ;
;![]() .
.
Тогда
![]() .
(6.30)
.
(6.30)
Зная добротность контура, можно судить об электромагнитных колебаниях, которые могут возникнуть в этом контуре.
