Контрольные вопросы к главе 2

1. Какую структуру должна иметь программа?

2. Верно ли, что в программе, написанной на языке Delphi, надо описывать все используемые в ней переменные?

3. Записать на Delphiследующие числа:

–27,8*10^-7; 10⁶; 0,5*10⁶; 6,38; 2; 4/1000.

4. Записать следующие числа без десятичного порядка:

–0.00027Е+4; 555Е-3; 1Е1.

5. Привести примеры целых чисел, не представимых на Delphi.

6. Записать на Delphi следующие формулы:a+bx+cyz; (1+x)²;cos³x²; |a+bx|;sin8x;log₂0,4x;arcctg10³;arcsinx;x⁵; (1+x)^1/3;x^-2;e^|x-y|;ln(1+3,3x);;tg³ x⁵;ctg²x³;;;

7. Вычислить значения выражения:

trunc(6,9); trunc(6,54); int(4,56);

frac(45,67); round(34,56); round(12,11);

round(–2,6); int(38,976); trunc(184,7).

8. Вычислить значение выражений:

20 div 5; 20 mod 7;

2 div 5; 2 mod 7.

9. Указать порядок выполнения операций в выражении:

a mod b + a div b*c/a.

10. Если у – вещественная переменная, а n – целая, то какие из следующих операторов присваи­вания правильные, а какие нет и почему:

y:=n+1; n:=y–1; n:=4.0;

y:=trunc(y); n:=n div 2; n:=sqr(sqr(n)).

y:=ydiv2;n:=n/2;

11. Какое значение будет иметь переменная х после выполнения операторов, если х:=10; х:=х+3?

12. С помощью каких средств языка Delphiможно осуществить ввод данных?

13. С помощью каких средств языка Delphi можно осуществить вывод данных?

14. Каким образом можно отредактировать форму, предложенную Delphi, с тем, чтобы создать свой проект?

Задания к лабораторной работе № 2

1. Вычислить дробную часть среднего геометрического трех заданных положительных чисел.

2. По заданным коэффициентам и правым частям системы уравнений 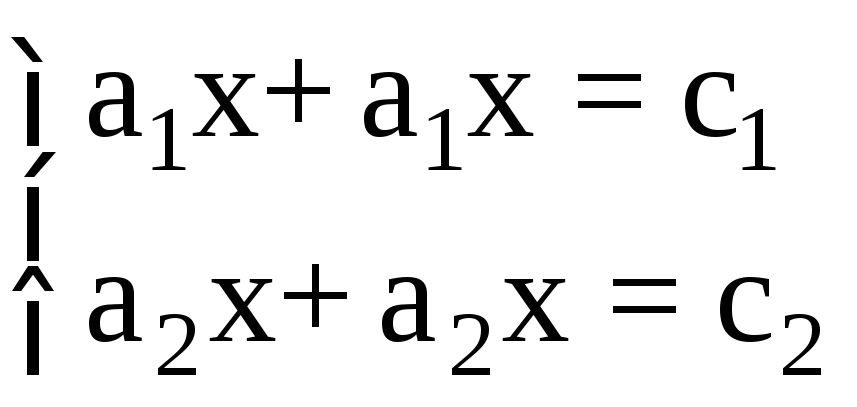найти ее решение в предположении, что определитель системы не равен нулю.

3. По координатам вершин некоторого треугольника найти его площадь и периметр.

4. По длинам двух сторон некоторого треугольника и углу (в градусах) между ними найти длину третьей стороны и площадь этого треугольника.

5. Найти произведение цифр заданного четырехзначного числа.

6. Определить число, полученное выписыванием в обратном порядке цифр заданного трехзначного числа.

7. Присвоить целой переменной d первую цифру из дробной части положительного вещественного числа х (так, если х=32,597, то d=5).

8. Целой переменной присвоить сумму цифр трехзначного целого числа k.

9. Идет k-я секунда суток. Определить, сколько полных часов (h) и полных минут (m) прошло к этому моменту (например, h=3 и m=40, если k=3*3600+40*60+57).

10. Даны катеты прямоугольного треугольника. Найти его периметр и площадь.

11. Даны два действительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.

12. Даны два действительных числа. Найти среднее арифметическое этих чисел и среднее геометрическое их модулей.

13. Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.

14. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

15. Найти площадь кольца, внутренний радиус которого равен 20, а внешний заданному числу r (r>20).

16. Даны основания и высота равнобедренной трапеции. Найти ее периметр и площадь.

17. Даны два числа. Найти их сумму, разность, произведение и частное от деления первого числа на второе.

18. Вычислить дробную часть среднего арифметического трех заданных положительных чисел.

19. По координатам вершин некоторого прямоугольника найти его площадь и периметр.

20. Дана сторона равностороннего треугольника. Вычислить площадь и периметр треугольника.

21. Дана сторона квадрата. В квадрат вписана окружность. Найти сторону и площадь квадрата, вписанного в эту окружность.

22. Дан радиус окружности. В окружность вписан квадрат. Найти площади окружности и квадрата.

23. Равносторонний треугольник задан координатами вершин. Найти площадь и периметр треугольника.

24. Даны x, y, z. Вычислить a, b, если:

25. Даны x, y, z. Вычислить a, b, если:

    a = y +	x	; b=(1 + tg2z/2)0.4.
    	y2 + |x2/y + x/4|

26. Даны x, y, z. Вычислить a, b, если:

    a =	2 cos(x-/6)	; b = 1 +	z2	.
    	1/21 + sin(y)		3 + z/5

27. Даны x, y, z. Вычислить a, b, если:

a =	1 + sin2(x + y)	+ x ; b = cos2(аrctg1/z) .
	2 + |x – 2x/(1 + xy)|

Примечания:

1. Сторона треугольника, где a,b– стороны треугольника;g– угол между сторонами a и b.

2. Площадь треугольника, гдеa,b,c– стороны треугольника;p– полупериметр.

3. Радиус вписанной в прямоугольный треугольник окружности r=s/p, где s – площадь треугольника; p – полупериметр треугольника.

4. Площадь окружности s= πr², длина окружностиl=π2r, гдеr– радиус окружности.