Контрольные вопросы к главе 7

1. Для чего предназначаются подпрограммы?

2. Что включает в себя заголовок процедуры?

3. Что включает в себя заголовок функции?

4. Какую структуру имеет процедура?

5. Какую структуру имеет функция?

6. Чем отличается процедура от функции?

7. Какая существует взаимосвязь между формальными и фактическими параметрами?

8. Какие существуют разновидности параметров подпрограмм?

9. Чем отличаются параметры-переменные от параметров-констант?

10. Чем отличаются параметры-значения от параметров-констант?

11. С какой целью используются открытые массивы?

12. В чем суть рекурсивного метода организации вычислений?

13. Какие достоинства и недостатки рекурсивного метода?

14. Каким образом реализуется косвенная рекурсия?

Задания к лабораторной работе № 7

1. Составить программу вычисления функции Yи суммыS, представляющей собой формулу разложения заданной функцииYв ряд. При составлении программы необходимо использовать процедуры или функции, основанные на нерекурсивном и рекурсивном методах вычислений.

Варианты заданий приведены ниже (табл. 7.2).

Примечания:

1. В первой графе содержится порядковый номер задания. Рекомендуется выбирать номер задания, соответствующий порядковому номеру фамилии студента в списке группы.

2. Во второй графе приводится формула функции Y.

3. В третьей графе помещается формула разложения функции Yв ряд.

4. В четвертой графе показан диапазон значения аргумента x, для которого следует выполнить вычисления. Рекомендуется вычислитьYиSдля 11 точек заданного диапазона измененияx.

Шаг изменения аргумента определить по формуле:

где х_н– начальное значениеx;,

х_к– конечное значениеx.

5. В пятой графе указано значение n – количество членов суммы S.

Таблица 7.2

Варианты заданий

Функция Y	Сумма S	Диапазон изменения аргумента	n
Y=3x		0,1x1	10
			40
		0,1x1	10
		1x2	15
		0,1x1	25
		0,1x1	10
		0,1x0,8	40
		0,1x1	20
		0,1x1	10
		0,2x1	10
		/5x	20
		0,1x1	10

Окончание табл. 7.2

Функция Y	Сумма S	Диапазон изменения аргумента	n
		0,1x1	20
		0,1x1	30
		0,1x0,5	40
		0,1x1	15
		0,1x1	35
		0,1x1	15
		-2x-0,1	40
		0,1x1	20
		0,1x0,8	40
		0,1x1	15
			40

2. Вычислить для заданных а и погрешностиeps, используя при условиирекуррентное соотношение:

3. Вычислить для заданных а и погрешностиeps, используя при условиирекуррентное соотношение Ньютона:

4. Вычислить для заданныхаи погрешностиeps, используя при условиирекуррентное соотношение Ньютона:

5. Число различных перестановок с повторениями, которые можно сделать из данных элементов, вычисляется по формуле

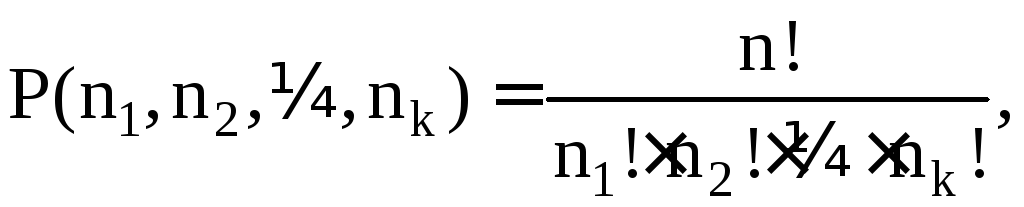
Например, число перестановок, которые можно сделать из букв слова «Миссисипи» (в слове всего 9 букв: 4 буквы «и», 3 буквы «с», 1 буква «м», 1 буква «п»), равноНаписать программу подсчета числа перестановок с повторениями. Задачу решить двумя способами: без применения рекурсии и с использованием рекурсивного метода.