Вариант 13

1. Найти дифференциальное уравнение и передаточную функцию тахогенератора постоянного тока при неизменном потоке возбуждения ЭДС в якоре относительно угла поворотаи напряжения якоряU₂, считая, что сопротивление нагрузки велико.

2. Построить АФЧХ для .

3. Построить ЛАЧХ и ЛФЧХ для приk=400 c^-1, Т = 25 мс.

4. Найти передаточную функцию замкнутой системы W_XY и записать дифференциальное уравнение для САУ:

где ;;;.

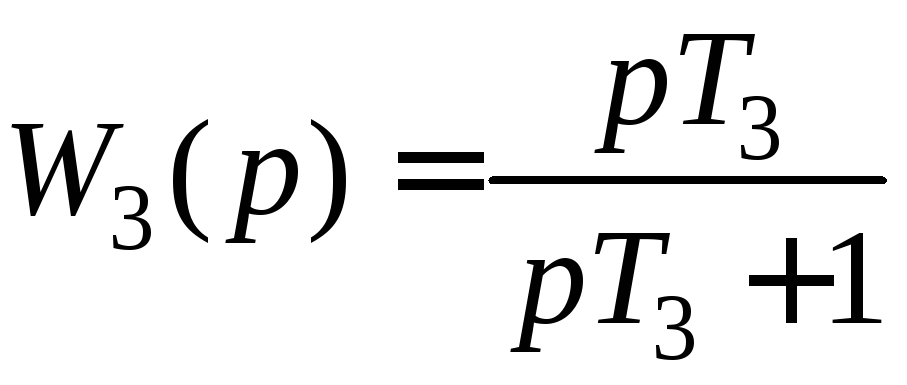5. C помощью критерия Гурвица определить, устойчива ли система, имеющая дифференциальное уравнение:

,

где k = 4 c^-1; Т₁ = 0,02 с; Т₂ = 0,01 с; Т₃ = 0,05 с.

6. Передаточная функция замкнутой САУ имеет вид

.

Определить устойчивость системы по критерию Михайлова.

7. Для структурной схемы САУ:

где ;;, оценить ее устойчивость по критерию Найквиста.

8. Передаточная функция САУ в разомкнутом состоянии

,

где k = 300 c^-1; Т₁ = 0,2 с; Т₂ = 0,05 с; Т₃ = 0,02 с.

Определить устойчивость замкнутой системы по логарифмическому критерию.

9. Методом D-разбиения выделить область устойчивости для САУ с передаточной функцией

при изменении параметра k.

10. Следящая система описывается уравнением

(Tp²+p+k)y (t)=(k_rp+k)x (t),

где Т = 0,005 с; k = 200 с^-1; k_r = 0,8.

Определить показатели качества системы при задающем воздействии в виде единичной ступенчатой функции 1(t) и нулевых начальных условиях.

Вариант 14

1. Найти передаточную функцию и дифференциальное уравнение пассивной электрической цепи относительно напряжений U_вх и U_вых.

2. Построить АФЧХ для при k=100 c^-2, T=0,2 c.

3. Построить ЛАЧХ и ЛФЧХ для .

4. Найти передаточную функцию замкнутой системы W_XF и записать дифференциальное уравнение для САУ:

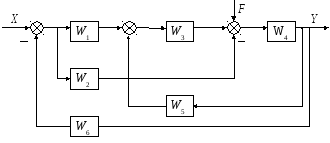
где ; ; ; ; ; 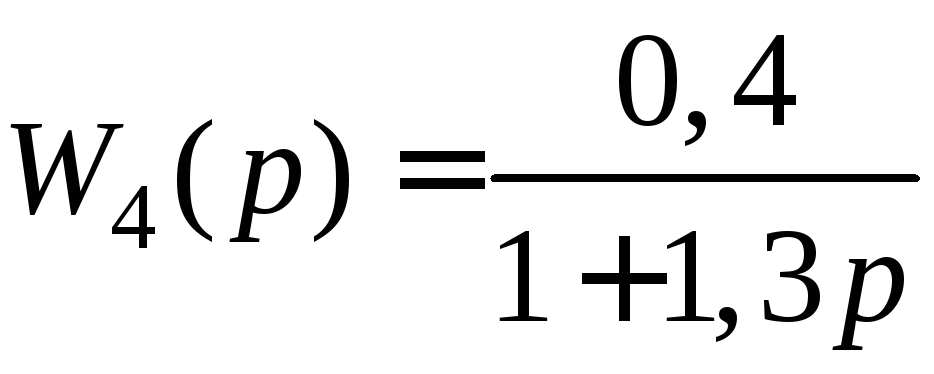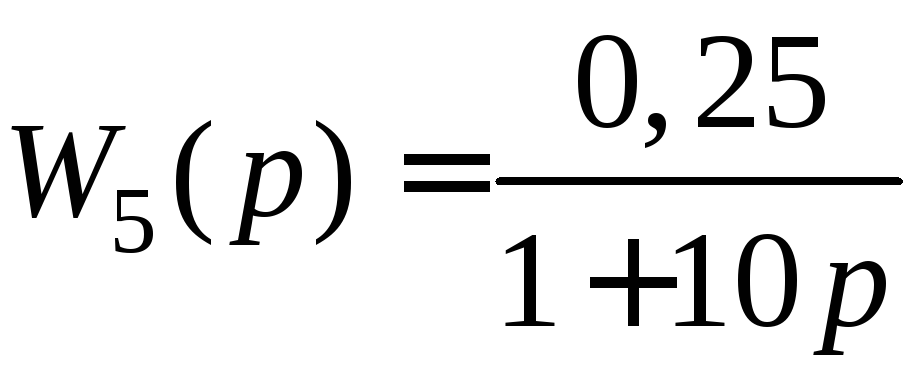W₆(p) = 1.

5. Характеристическое уравнение замкнутой САУ имеет вид

.

Оценить устойчивость системы по критерию Гурвица.

6. Передаточная функция разомкнутой САУ имеет вид

,

где k – общий коэффициент усиления разомкнутой системы; Т₁ = 0,5 с; Т₂ = 0,1 с; Т₃ = 0,02 с.

С помощью критерия устойчивости Михайлова определить значение общего коэффициента разомкнутой системы, при котором система оказывается на границе устойчивости.

7. Для структурной схемы САУ:

где ;;, оценить устойчивость по критерию Найквиста.

8. Переходная функция САУ в разомкнутом состоянии

,

где

Определить устойчивость замкнутой системы по логарифмическому критерию.

9. Методом D-разбиения на плоскости двух варьируемых параметров иT САУ выделить область устойчивости системы с передаточной функцией .

10. Характеристическое уравнение САР имеет вид

.

Определить показатели качества системы.

Вариант 15

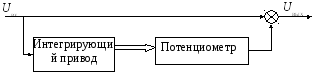
1. Найти передаточную функцию и дифференциальное уравнение звена, построенного на базе интегрирующего привода.

2. Построить АФЧХ для при k = 50 c^-2.

3. Построить ЛАЧХ и ЛФЧХ для приТ = 50 мс.

4. Найти передаточную функцию замкнутой системы W_XF и записать дифференциальное уравнение для САУ:

где ;;;;.

5. Характеристическое уравнение замкнутой САУ имеет вид

.

Оценить устойчивость системы по критерию Гурвица.

6. Передаточная функция разомкнутой системы САУ имеет вид

,

где k – общий коэффициент усиления разомкнутой системы; Т₁ = 0,05 с; Т₂ = 0,2 с; Т₃ = 0,1 с; .

С помощью критерия устойчивости Михайлова определить значение общего коэффициента разомкнутой системы, при котором система оказывается на границе устойчивости.

7. Передаточная функция электромеханической следящей системы в разомкнутом состоянии имеет вид

,

где k = 100 c^-1; Т_м = 0,1 с; Т_у = 0,02 с.

Определить устойчивость электромеханической следящей системы, используя критерий устойчивости Найквиста.

8. Для структурной схемы САУ:

где ;;;

оценить устойчивость по логарифмическому критерию.

9. Методом D-разбиения на плоскости двух варьируемых параметров k и T системы выделить область устойчивости системы с передаточной функцией .

10. Передаточная функция разомкнутой следящей системы

.

Определить показатели качества замкнутой системы при задающем воздействии в виде единичной ступенчатой функции 1(t) и нулевых начальных условиях.