Лекции_РЭС / Лекция №4 Случайные сигналы. Корреляционный анализ сигналов

Лекция №4 Случайные сигналы. Корреляционный анализ сигналов

В последние годы широкое развитие получила статистическая радиотехника, что объясняется необходимостью изучения явлений при передаче сообщений в условиях, когда детерминированное описание сигналов невозможно. Статистическая радиотехника рассматривает вопросы приема сигналов в шумах и базируется на аппарате теории вероятностей и случайных процессов. Случайное изменение параметров полезных сигналов обусловлено воздействием на них дестабилизирующих факторов, таких, как случайный характер модуляции, нестабильность частоты и т. д. Такой же вид имеют и шумы. Поэтому они объединены и терминологически — понятия «случайный сигнал» и «случайный процесс» используются как синонимы и часто обозначаются как «случайные процессы». При статистическом подходе к этой проблеме не обязательно определять точный результат одного исследования, а можно основываться на анализе множества опытов и найти закономерности, характеризующие случайный процесс в среднем.

Важное значение в радиотехнике, наряду с узкополосными, имеют широкополосные сигналы. К ним относятся и шумоподобные (pseudonoise) сигналы, называемые так по причине близости их спектра к белому шуму. отличительной чертой случайного сигнала является то, что его мгновенные значения заранее не предсказуемы. В отличие от детерминированных сигналов, значения случайных сигналов в произвольные моменты времени не могут быть вычислены достоверно, а могут быть только предсказаны в определенном диапазоне значений с определенной вероятностью, меньшей единицы. Важно и то, что чаще всего наблюдают относительно небольшие отклонения амплитудных значений случайного сигнала от некоторого среднего уровня; чем больше отклонения по абсолютному значению, тем реже их наблюдают. Уже в этом проявляется статистическая закономерность. Располагая сведениями о вероятностях флуктуации различного уровня, удается создать математическую модель случайного колебания, приемлемую для детального анализа случайного процесса. В общем случае в радиотехнике и теории связи существуют два основных класса сигналов, нуждающихся в вероятностном описании. Во-первых, практически случайными являются все реальные сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, прибегают к вероятностным моделям. Во-вторых, шумы — хаотически изменяющиеся во времени электромагнитные колебания, возникающие в разных физических с истемах из-за беспорядочного движения носителей заряда.

Рис. 4.1. Различные виды случайных процессов:

а — реализация непрерывного шума; б — «телеграфный» сигнал;

в — случайный процесс на входе детектора; г — импульсный случайный сигнал

Вероятностное представление случайных величин и процессов

В теории сигналов исследуемый случайный процесс представляют бесконечным множеством некоторых временных функций. Рассмотрим (для наглядности низкочастотный) случайный процесс, состоящий из множества случайных сигналов X₁(t), X₂(t), ..., X_k(t), ... , называемых реализациями случайного процесса (рис. 4.2), и аналитически описываемый некоторой обобщающей его случайной функцией X(t). Совокупность всех реализаций случайного процесса называют ансамблем (рис. 4.2, а). Ансамбль реализаций — математическая абстракция, модель рассматриваемого процесса, но конкретные реализации (см., например, k-ю реализацию на рис. 4.2, б), используемые на практике, представляют физические объекты или явления и входят в ансамбль как его неотъемлемая часть. Типичными примерами случайных процессов в радиотехнике являются тепловые шумы в пассивных и активных элементах, действием которых сопровождается работа в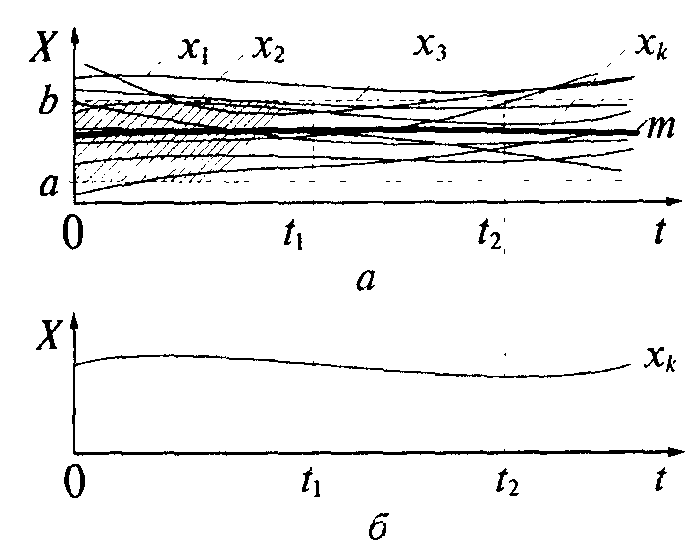 сех радиотехнических устройств.

Рис. 4.2. Реализации случайного процесса:

а — ансамбль; б — k-я реализация

Отметим на рис. 4.2 некоторый момент времени t = t₁. Значения, которые могут принимать конкретные реализации x₁(t), x₂(t), ..., x_k(t) всего ансамбля в заданный момент времени t₁, образуют совокупность случайных величин x₁(t₁), x₂(t₁), ..., x_k(t₁), которую обозначим случайной величиной X(t₁). Эту величину X(t₁), отражающую совокупность всех возможных значений реализаций случайного процесса X(t₁) в момент времени t₁, называют сечением случайного процесса. Случайная величина X(t₁) может иметь любые заранее неизвестные значения в некотором интервале изменения амплитуд.

Одной из важных одномерных характеристик случайной величины X(t₁) является интегральная функция распределения (проще, функция распределения) или функция распределения вероятности (cumulative distribution function, CDF) F(x). Численно эта функция определяется как вероятность того, что все значения случайной величины X(t₁) не превышают некоторого заданного уровня х:

(4.1)

где Р — символ, отражающий вероятность.

Основные свойства интегральной функции распределения вероятности:

• для случайной величины X(t₁), имеющей любые вещественные значения, функцию распределения определяют на интервале 0 <F(x) < 1 при - - ∞<х<<∞;

• функция распределения F(x) не уменьшается при возрастании аргумента х;

• для интегральной функции распределения F(x) справедливо равенство

Если случайная величина X(t₁) является непрерывной во времени, то зачастую вместо функции распределения удобнее пользоваться ее производной

(4.2)

получившей название одномерной плотности распределения вероятности (или, проще, плотности вероятности —probability density function, PDF).

Зададим некоторый интервал а - b изменения мгновенного значения х случайного процесса (см. рис. 4.2). Тогда из (4.2) следует, что плотность вероятности

(4.3)

— есть вероятность попадания случайной величины X(t₁) в заданный интервал.

Пусть параметр а -> - ∞, а b принимает текущее значение переменной х. В этом случае интегральная функция распределения примет вид:

4.4

Одномерная плотность вероятности всегда неотрицательная величина и удовлетворяет условию нормировки

4.5

Площадь под кривой плотности вероятности р(х, t₁) всегда равна единице.

Если φ(х) — известная функция от х (исхода случайного испытания), то по определению ее среднее значение (average value; часто mean value)

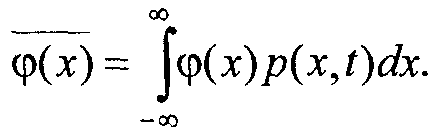4.6

Момент n-го порядка случайной величины X(t) есть среднее значение n-й степени случайной переменной

4.7

Математическое ожидание-момент первого порядка, и дисперсия - центральный момент второго порядка.

4.9 4.10

Дисперсия (variance), или второй центральный момент, определяется как математическое ожидание квадрата отклонения случайного процесса от его математического ожидания

4.11

При нулевом математическом ожидании дисперсия характеризует среднюю мощность флуктуации случайного процесса.

Среди двумерных функций распределения особое место занимает второй смешанный центральный момент — функция корреляции (корреляционная функция), которая характеризует статистическую связь между значениями одного и того же случайного процесса в два различных момента времени.

Функция корреляции

4.12

представляет собой меру связи между сечениями случайного процесса, взятыми в моменты времени t₁ и t₂.

Когда t₁ = t₂, т. е. при совмещении сечений случайного процесса, функция корреляции численно равна дисперсии

4.13

Случайные процессы, изучаемые в радиотехнике, часто обладают следующим специфическим свойством: их функция корреляции стремится к нулю с увеличением временного сдвига т (кстати, это является достаточным условием эргодичности процесса). Чем быстрее убывает функция R(τ), тем слабее оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.