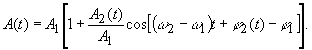Лекции_РЭС / Узкополосные системы связи и сигналы

2.7.5 Узкополосный сигнал

Сигнал называется узкополосным (УПС), если ширина его спектра значительно меньше средней частоты (рис.13):

Рис. 13

Типичными представителями УПС являются модулированные радиосигналы. К УПС можно также отнести несколько радиосигналов со своими несущими, занимающие вместе достаточно узкую полосу частот.

В первом приближении для анализа прохождения УПС через радиоэлектронные цепи такой сигнал можно представить гармоническим на средней частоте. Более лучшее приближение дает представление УПС в виде квазигармонического колебания, у которого медленно (по сравнению с ) меняются мгновенные амплитуда и частота. В этом случае полагается, что за достаточно короткое время (меньшее, чем изменения амплитуды и частоты), сигнал можно считать гармоническим.

В общем случае УПС можно представить в виде

где и -медленно меняющиеся функции времени.

Для классических АМ и ЧМ колебаний средняя частота совпадает с несущей частотой сигнала. Для однозначного и наиболее оптимального выбора применяется аппарат преобразования Гильберта, согласно которому для заданного УПС находится сопряженная функция ,определяемая как

при этом

Огибающая, определённая таким образом, совпадает с сигналом в моменты времени, где ,т.е. имеют общие касательные, причем в точках касания функция близка к максимумам (Рис.14):

Рис. 14

Для сигнала вида сопряженная по Гильберту функция равна а для .

Исходя из этих соотношений для гармонического сигналаогибающая и частота равны соответственно:

как и следовало ожидать. Если же выбрать произвольным образом среднюю частоту, то даже для гармонического сигнала можно получить некую достаточно сложную огибающую, не соответствующую действительности.

Рассмотрим в качестве примера УПС, состоящий из суммы гармонических составляющих:

Для такого сигнала

откуда

После преобразований можно получить следующее выражение для мгновенной частоты

Для двухчастотного сигнала (N=2) имеем

Таким образом, сумму двух близко расположенных по частоте () сигналов можно записать в виде квазигармонического колебания:

Рис.15 иллюстрирует примерный вид сигнала, состоящего из двух гармонических сигналов с равными амплитудами (==).

Рис. 15

Ниже на рис. 16 и рис. 17 приведены нормированные графики одного периода огибающей и мгновенной частоты: бигармонического сигнала для , 0,5 и 0,1.

Рис. 16

Из графиков рис. 15, 16 и 17 видно, что при взаимодействии двух сигналов с равными амплитудами огибающая амплитуд меняется от удвоенной амплитуды каждого до нуля. Причем в нуле огибающей фаза скачком меняется на ,что формально означает переход через бесконечность (разрыв) мгновенной частоты, а в остальное время

При уменьшении амплитуды одного из сигналов мгновенная частота ( рис.17 ) непрерывно меняется и при малом k средняя частота близка к частоте большего сигнала.

Рис. 17

При малом k огибающую можно представить в приближенном виде

откуда видно, что огибающая в этом случае линейно зависит от амплитуды малого сигнала при постоянной амплитуде большого. Если малый сигнал в свою очередь будет квазигармоническим

т.е.

то

Таким образом результирующая огибающая содержит линейную информацию об изменении амплитуды и фазы малого сигнала, что дает возможность в приемнике выделить эту информацию без нелинейных искажений.

© Андреевская Т.М., РЭ, М