Лекции_РЭС / Лекция №6 модулированные сигналы

8

Лекция № 6 Модулированные сигналы

Под модуляцией понимают процесс (медленный по сравнению с периодом несущего колебания), при котором один или несколько параметров несущего колебания изменяют по закону передаваемого сообщения. Получаемые в процессе модуляции колебания называют радиосигналами. В зависимости от того, какой из названных параметров несущего колебания подвергается изменению, различают два основных вида аналоговой модуляции: амплитудную и угловую. Последний вид модуляции, в свою очередь, разделяется на частотную и фазовую. В современных цифровых системах передачи информации широкое распространение получила квадратурная (амплитудно-фазовая, или фазоамплитуд- ная — ФАМ; amplitude phase modulation) модуляция, при которой одновременно изменяются и амплитуда и фаза сигнала. Этот тип модуляции относят как к аналоговым, так и цифровым видам.

В радиосистемах часто применяются и будут применяться различные виды импульсной и цифровой модуляции, при которой радиосигналы представляются в виде так называемых радиоимульсов.

Радиосигналы с аналоговыми видами модуляции В процессе амплитудной модуляции несущего колебания (1)

его амплитуда должна изменяться по закону: (2)

где U_H — амплитуда несущей в отсутствие модуляции; ω₀ — угловая частота; φ₀ — начальная фаза; ψ(t) = ω₀+ φ₀ — полная (текущая или мгновенная) фаза несущей; k_А — безразмерный коэффициент пропорциональности; e(t) — модулирующий сигнал. U_H(t) в радиотехнике принято называть огибающей амплитудно-модулированного сигнала (АМ-сигнала).

Подставив (2) в (1) получим общую формулу АМ- сигнала (3)

Однотональная амплитудная модуляция если модулирующий сигнал — гармоническое колебание (4)

где Е₀ — амплитуда; Ω = 2π/Т₁ = 2πF — угловая частота модуляции; F —

циклическая частота модуляции; Т₁ — период модуляции; θ₀ — начальная фаза.

Подставив формулу (4) в соотношение (3), получим выражение для АМ-сигнала (5)

О бозначив через ∆U = k_AE₀- максимальное отклонение амплитуды АМ- сигнала от амплитуды несущей U_H и проведя несложные выкладки, получим (6)

где

— коэффициент или глубина амплитудной модуляции.

Спектр АМ-сигнала. Применив в выражении (5) тригонометрическую формулу произведения косинусов, после несложных выкладок получим (7)

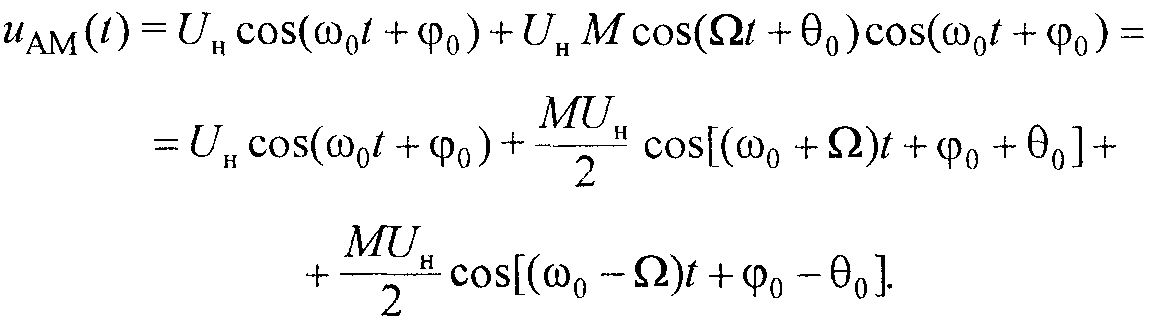
Из формулы (7) видно, что при однотональной амплитудной модуляции спектр АМ-сигнала состоит из трех высокочастотных составляющих. Первая из них представляет собой исходное несущее колебание с постоянной амплитудой U_H и частотой с ω₀ . Вторая и третья составляющие характеризуют новые гармонические колебания, появляющиеся в процессе амплитудной модуляции и отражающие передаваемый сигнал. Колебания с частотами ω₀ + Ω и ω₀ - Ω называются соответственно верхней (upper sideband — USB) и нижней (lower sideband — LSB) боковыми составляющими.

Реальная ширина спектра АМ-сигнала при однотональной модуляции (8)

(9)

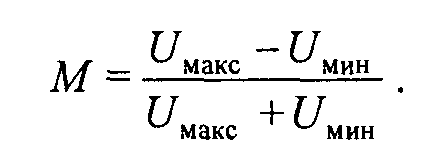
На практике однотональные АМ-сигналы используются либо для учебных, либо для исследовательских целей. Реальный же модулирующий сигнал имеет сложный спектральный состав. Математически такой сигнал, состоящий из N гармоник, можно представить тригонометрическим рядом N (10)

Здесь амплитуды гармоник сложного модулирующего сигнала E_i произвольны, а их частоты образуют упорядоченный спектр Ω₁ < Ω₂ < ...< Ω_i < ...< Ω_N. В отличие от ряда Фурье частоты Ω_i не обязательно кратны друг другу. Подставляя (10) в (3), после несложных преобразований, получим выражение АМ-сигнала с начальной фазой несущего ф0 = О (11)

(12)

Совокупность парциальных (частичных) коэффициентов модуляции. Эти коэффициенты характеризуют влияние гармонических составляющих модулирующего сигнала на общее изменение амплитуды высокочастотного колебания. Воспользовавшись тригонометрической формулой произведения двух косинусов и проделав несложные преобразования, запишем (11) в виде (13)

Рис. 2. Спектральные диаграммы при модуляции сложным сигналом:

а — модулирующего сигнала; б — АМ-сигнала

Ширина спектра сложного АМ-сигнала равна удвоенному значению наивысшей частоты в спектре модулирующего сигнала Ω_N, т. е. (14)

Частотная модуляция

При частотной модуляции (frequency modulation; FM) мгновенное значение несущей частоты ω(t) связано с модулирующим сигналом e(t) зависимостью (15)

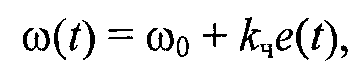
здесь k_Ч — размерный коэффициент пропорциональности между частотой и напряжением, рад/(В-с).

Полную фазу ЧМ-сигнала в любой момент времени t определим путем интегрирования мгновенной частоты, выраженной через формулу (15),

Рис. 3. Частотная однотональная модуляция:

а — несущее колебание; б — модулирующий сигнал; в — ЧМ-сигнал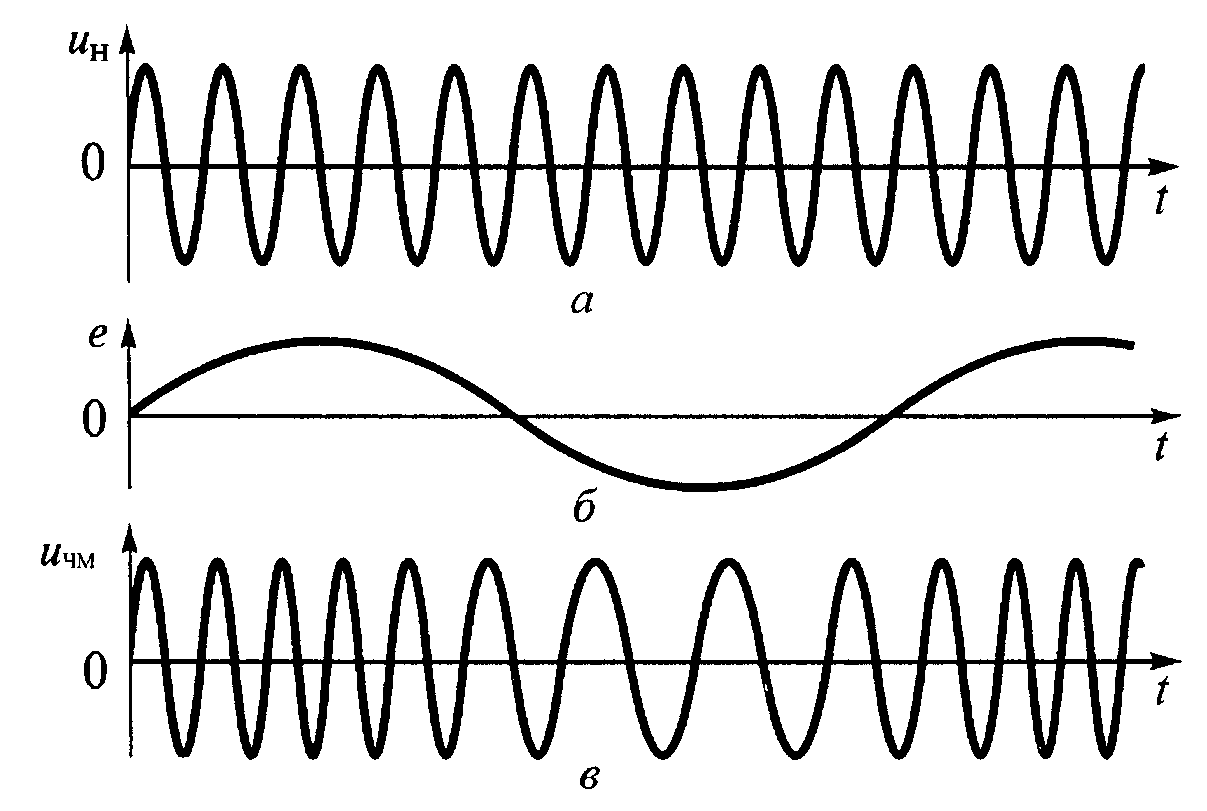

(16)

- максимальное отклонение частоты от значения ω₀, или девиация частоты (frequency deviation) при частотной модуляции;

— максимальное отклонение от текущей фазы ω₀t или девиация фазы несущего колебания называется индексом частотной модуляции (index of frequency modulation). Данный парамер определяет интенсивность колебаний начальной фазы радиосигнала.

С учетом полученных соотношений (1) и (16) частотно-модулированный сигнал запишется в следующем виде:

Спектр ЧМ-сигнала при однотональной модуляции. Преобразуем полученное выражение (17)

Спектр ЧМ-сигнала при m«1 (такую угловую модуляцию называют узкополосной). В этом случае имеют место приближенные равенства: (18)

Подставив формулы (18) в выражение (17), после несложных математических преобразований получим (при начальных фазах модулирующего и несущего колебаний θ₀ = 0 и φ₀ = 0): (19)

Видим, что по аналитической записи спектр ЧМ-сигнала при однотональной модуляции напоминает спектр АМ- сигнала и также состоит из несущего колебания и двух боковых составляющих с частотами (ω₀+ Ω) и (ω₀- Ω) причем и амплитуды их рассчитываются аналогично (только вместо коэффициента амплитудной модуляции М в формуле для ЧМ-сигнала фигурирует индекс угловой модуляции m). Но есть и принципиальное отличие, превращающее амплитудную модуляцию в частотную, знак минус перед одной из боковых составляющих.

Спектр ЧМ-сигнала при m> 1. Из математики известно (20) (21)

где J_n(m) — функция Бесселя 1 -го рода n-го порядка.

В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой формулой (22)

Ряды (20) и (21) подставим в формулу (17), а затем заменим произведение косинусов и синусов полусуммами косинусов соответствующих аргументов. Тогда, с учетом (22), получим следующее выражение для ЧМ-сигнала (23)

Итак, спектр ЧМ-сигнала с однотональной модуляцией при индексе

модуляции m > 1 состоит из множества высокочастотных гармоник: несущего колебания и бесконечного числа боковых составляющих с частотами ω₀+ nΩ. и ω₀-nΩ, расположенными попарно и симметрично относительно несущей частоты ω₀.

При этом, исходя из (22), можно отметить, что начальные фазы боковых колебаний с частотами ω₀+ nΩ. и ω₀-nΩ совпадают, если m — четное число, и отличаются на 180°, если m — нечетное. Теоретически спектр ЧМ- сигнала (так же и ФМ-сигнала) бесконечен, однако в реальных случаях он ограничен. Практическая ширина спектра сигналов с угловой модуляцией

ЧМ- и ФМ-сигналы, применяемые на практике в радиотехнике и связи, имеют индекс модуляции m>> 1, поэтому

П олоса частот ЧМ-сигнала с однотональной модуляцией равна удвоенной девиации частоты и не зависит от частоты модуляции.

Сравнение помехоустойчивости радиосистем с амплитудной и угловой модуляцией. Следует отметить, что радиосигналы с угловой модуляцией имеют ряд важных преимуществ перед амплитудно-модулированными колебаниями.

1. Поскольку при угловой модуляции амплитуда модулированных колебаний не несет в себе никакой информации и не требуется ее постоянства (в отличие от амплитудной модуляции), то практически любые вредные нелинейные изменения амплитуды радиосигнала в процессе осуществления связи не приводят к заметному искажению передаваемого сообщения.

2. Постоянство амплитуды радиосигнала при угловой модуляции позволяет полностью использовать энергетические возможности генератора несущей частоты, который работает при неизменной средней мощности колебаний.