Лекции_РЭС / Линейные цепи

Элементная база линейных цепей.

Линейные четырехполюсники

По функциональному назначению линейные цепи делят на

а) дифференцирующие цепи и устройства;

б) интегрирующие;

в) частотно-избирательные цепи;

г) линейные усилители и фильтры.

Д ифференцирующая цепь - последовательной электрическая RC-цепь, на входе которой действует напряжение u_BX(t), а выходное напряжение u_BЫX(t), снимается с резистора R

Дифференцирующая цепь: а — схема; б — амплитудно-частотная характеристика (АЧХ)

На основании второго закона Кирхгофа

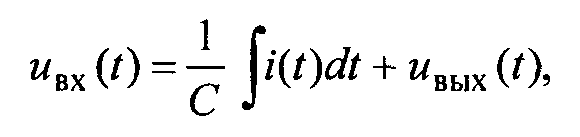
i(t) -мгновенное значение напряжения для всей линейной цепи

Продифференцируем по времени обе части этого соотношения:

У множив и поделив первое слагаемое в правой части на R и учитывая, что u_BЫX(t)=i(t)R, получим

Обозначим – постоянная времени цепи, получим

Если постоянная времени настолько мала, что выполняется условие

то окончательно получим

Таким образом анализируемая RС-цепь при малых τ_α может осуществлять линейную операцию дифференцирования поданного на нее сигнала.

Чтобы определить частотный коэффициент передачи дифференцирующей цепи, запишем комплексную амплитуду тока:

Выразив комплексную амплитуду выходного напряжения через ток U_BЫX = IR, находим частотный коэффициент передачи

Модуль частотного коэффициента передачи,

нижняя граничная частота полосы пропускания (мощность выходного сигнала убывает в 2 раза)

верхнюю частоту спектральной плотности прямоугольного видеоимпульса принято приближенно ограничивать значением ω_И = 2π/τ_И. Тогда условие для соотношения частот ω_Н > ω_И можно записать в виде τ_α << τ_И /(2π), или как τ_α<<τ_И .

При больших отношениях τ_α/τ_И линейную электрическую RC-цепъ применяют как разделительную, разделяющую цепи переменного и постоянного токов, а при малых τ_α/τ_И — как дифференцирующую.

Интегрирующая цепь - последовательная электрическая RC-цепь, на входе которой действует напряжение u_BX(t), а выходное напряжение u_BЫX(t), снимается с емкости С.

И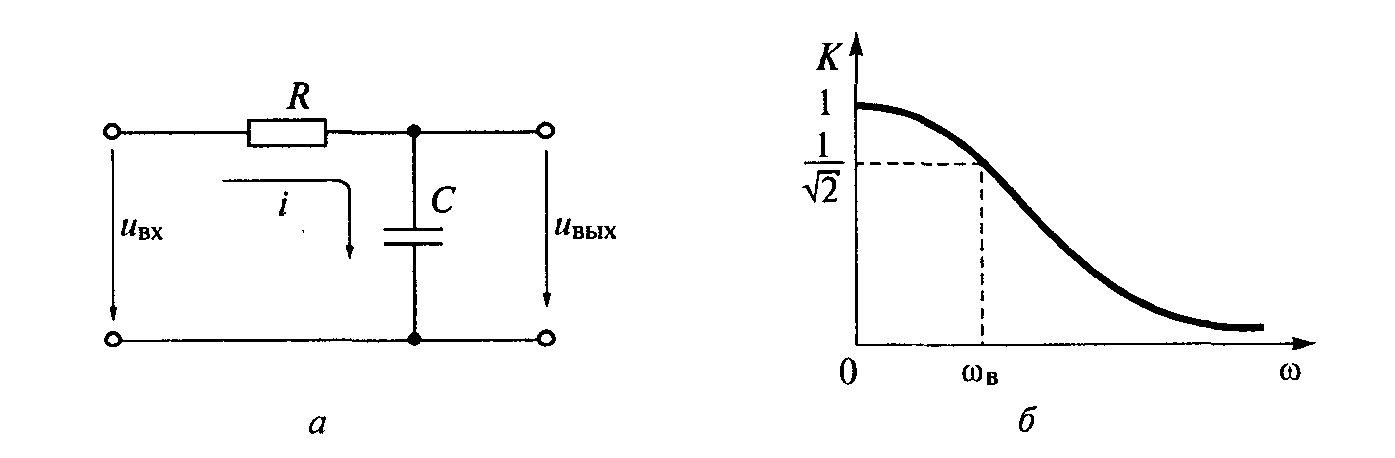 нтегрирующая цепь: а — схема; б — амплитудно-частотная характеристика (АЧХ)

Используя аналогию с формулой для дифференцирующей цепи, запишем

Если τ_α настолько велика_, что

То

Интегрируя получаем

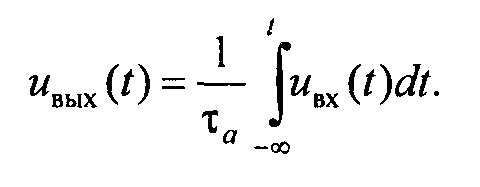
Для определения частотного коэффициента передачи интегрирующей цепи запишем комплексную амплитуду тока через комплексное входное напряжение

Т.к.

Получим

Определив модуль К(ω) находим АХЧ

И з условия К(ω_В)=1/(2)^0,5 можно определить верхнюю граничную частоту полосы пропускания интегрирующей цепи

Из графика для К(ω) следует, что интегрирующая цепь не пропускает высокочастотные составляющие спектра входного сигнала, поэтому в радиоэлектронных устройствах их используют в качестве так называемых сглаживающих (smoothing), или низкочастотных, фильтров.

Резонансные цепи – предназначены для выделения полезного сигнала из смеси побочных сигналов и шумов.

Последовательный колебательный контур.

Запишем полное входное сопротивление (импеданс — устаревшее) контура

Приняв Z =0, находим резонансную частоту контура (формула Томсона)

На резонансной частоте сопротивление контура актичвно и равно R. На любой другой частоте

где ρ –характеристическое сопротивление контура (сопротивление емкости или индуктивности на частоте резонанса).

Преобразуем Z (импеданс) к виду

Можно показать, что модуль частотного коэффициента передачи для малой абсолютной расстройки частоты контура относительно частоты входного сигнала. ∆ω = ω - ω_Р имеет вид

Данная функция представляет собой АЧХ контура, графически отображаемую в виде резонансной кривой.

Полоса пропускания контура определяется из условия К_I(ω)≥ 1/(2)^0,5. исторически её принято записывать через 2∆ω_Р

Так как на частоте резонанса напряжения на контуре U_ВХ= I_РR, Uc =I_Р ρ, то

Итак, при настройке контура в резонанс амплитуда напряжения на конденсаторе (или индуктивности) в Q раз больше амплитуды входного напряжения. Поэтому резонанс в последовательном контуре называют резонансом напряжений.

Параллельный колебательный контур. Такой контур состоит из параллельно соединенных индуктивности L и емкости С, а в цепь индуктивности включено сопротивление ее потерь R.

П олное входное сопротивление контура

Аналитически АЧХ параллельного контура отражается зависимостью нормированного по резонансному сопротивлению модуля входного сопротивления от величины абсолютной расстройки

Фазо-частотная характеристика (ФЧХ) параллельного контура определяется следующим выражением

Частотный коэффициент передачи контура по току нетрудно определить, вычислив отношение тока емкости (индуктивности) к входному току. На резонансной частоте этот параметр выразится простой формулой

Итак, на резонансной частоте ток в параллельном контуре в Q раз больше входного тока. Поэтому говорят о резонансе токов в параллельном контуре. Полоса пропускания параллельного контура определяется той же формулой, что и последовательного.

Связанные контуры. Позволяют существенно повысить частотную избирательность радиотехнических устройств, в которых удается получать близкую к идеальной (прямоугольной) форму АЧХ. Простейшими многоконтурными частотно-избирательными цепями являются два связанных колебательных контура.

Одним из основных параметров связанных контуров является коэффициент связи К_СВ. Для связанных контуров с индуктивной связью К_СВ = M/L, а с емкостной —

К_СВ = С/(С + С_СВ). Наиболее же важным параметром обычно считают фактор связи

Ас = К_СВ Q. При Ас < 1 связь называют слабой, а при Ас>1 — сильной.

А ЧХ связанных контуров определяется модулем коэффициента передачи К(ω)

Колебательные системы из большого числа связанных контуров называются фильтрами сосредоточенной селекции. С их помощью удается получить амплитудно-частотную характеристику, еще более приближающуюся к прямоугольной форме.

А ЧХ индуктивно связанных контуров

Неискажающая передача сигналов через линейные цепи. Рассмотрим идеальный линейный четырехполюсник, частотный коэффициент передачи которого теоретически определяется функцией вида

где К_Н=К(ω) – постоянный коэффициент; t_С=φ(ω)/ ω – некоторый момент времени (текущее время). Видим, что АЧХ равномерна, а ФЧХ – линейна в бесконечной полосе частот

Можно показать, что колебание на выходе идеального линейного четырехполюсника с точностью до постоянного коэффициента К_Н повторяет смещенный на определенное время входной сигнал.

идеальный линейный четырехполюсник, обладающий равномерной АЧХ и линейной ФЧХ в бесконечной полосе частот, теоретически осуществляет передачу радиотехнических сигналов без искажений. В практических линейных цепях даже в полосе пропускания АЧХ не всегда равномерна, а АЧХ — не строго линейна. Но важной особенностью линейных цепей является то, что при прохождении через них сигналов не нарушается форма ни одной гармонической составляющей, а может изменяться лишь их амплитуда и начальная фаза. Поэтому такие искажения в линейных цепях относят к классу линейных (иначе, частотных).