Параллельные проекции

По этой причине в проектировании, конструировании продолжают широко использовать параллельные проекции, которые разделяются на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости.

В ортографическихпараллельных проекциях эти направления совпадают, а косоугольныхпроекциях они не совпадают.

Наиболее широко используемыми видами ортографических проекций являются вид спереди, сверху, сбоку, в которых картинная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проецирования. Поскольку каждая проекция отображает лишь одну строну объекта, часто совсем непросто представить себе пространственную структуру проецируемого объекта, даже если рассматривать несколько проекций одного объекта вместе.

Вслучаеаксонометрическихпроекций используются проекционные плоскости не перпендикулярные главным координатным осям, поэтому на них изображены сразу несколько сторон объекта, но в отличии от центральной проекции здесь укорачивание постоянно и сохраняется параллельность прямых, углы изменяются.

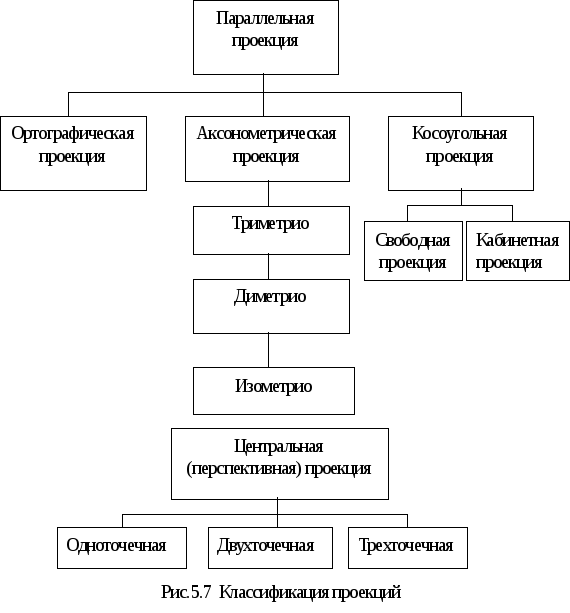
Каждый из этих двух классов проекций (центральная и параллельная) разбивается на несколько подклассов в зависимости от взаимного расположения картинной плоскости, координатных осей, направления проецирования и нормали к картинной плоскости. На 5.7 показана классификация параллельной и центральной проекций.

Рассмотрим некоторые математические соотношения, определяющие получение проекции на картинную плоскость. При ортографическойпроекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна одной их них. Матрица проецирования вдоль осиX плоскостьYOZможет быть записана в виде:

для случая x=0,

если же x=d, применяя преобразование сдвига, получаем преобразование проецирования вида

то есть, координатой точки на картинной плоскости при ортографическом режиме параллельного проецирования будет абсцисса x=d.

Аналогично для картинных плоскостей параллельных соответственно координатным плоскостям XOY и ZOX, приp  0иq  0, гдеpиq сдвиг картинных плоскостей вдоль осейZиY (направление сдвига учитывается введением знака “-” при соответствующей величине), запишем

При аксонометрическомпроецировании проецирующие прямые перпендикулярны картинной плоскости. При этом в зависимости от взаимного расположения плоскости проецирования и координатных осей имеем три варианта проекций:

• триметрио – нормаль к картинной плоскости образует с осями координат попарно различные углы;

• диметрио – два угла между нормалью к картинной плоскости и осями координат попарно равны;

• изометрио – все углы между нормалью к картинной плоскости и осями координат равны.

Каждая из трех определенных выше проекций получается конкатенацией поворотов, за которыми выполняется ортографическое проектирование, например, при реализации режима диметрио осуществляется поворот на угол вокруг оси ординат и на угол вокруг оси абсцисс, а затем проецирование вдоль осиZ

Аффинные преобразования в пространстве.

Рассмотрим вид формул аффинного преобразования для пространственного представления точки (случай 3Dграфики). В этом случае по аналогии с двухмерным представлением трехмерное позиционирование точки координатамиx, y, z представим в однородном описанииx, y, z, 1. То есть, каждая точка пространства (кроме 0) может быть задана четверкой одновременно не равных нулю чисел и эта четверка чисел однозначно определяет положение точки в пространстве с точностью до постоянного множителя. Подобное представление дает возможность, используя матричное представление решать сложные трехмерные задачи.

Любое аффинное преобразование в трехмерном пространстве может быть представлено суперпозицией матриц вращения, масштабирования и переноса¹. Полезно рассмотреть их представление в матричном виде, порядок которых равен четырем.

Трехмерный перенос представляется матрицей вида

, то

есть.

Масштабирование можно записать аналогичным образом

, поскольку

Матрица поворота, записанная для двухмерного случая, является поворотом вокруг оси z

.

Матрица поворота вокруг оси x записывается в виде:

.

Матрица поворота, относительно оси z имеет вид:

Замечание.Вращение в пространстве не коммутативно, поэтому порядок в котором осуществляется вращение является весьма существенным.

Интересно рассмотреть вид матриц отражения относительно трех плоскостей XOY, XOZ, Y0Z.

В первом случае матрица отражения имеет вид

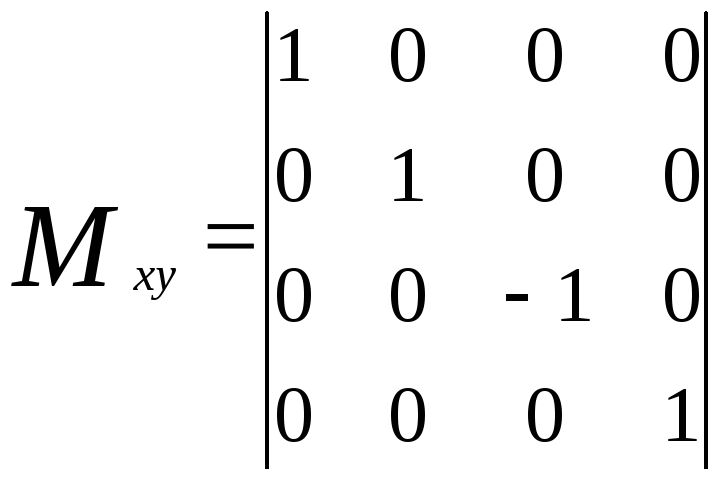
Отражение относительно плоскости YOZописывается матрицей

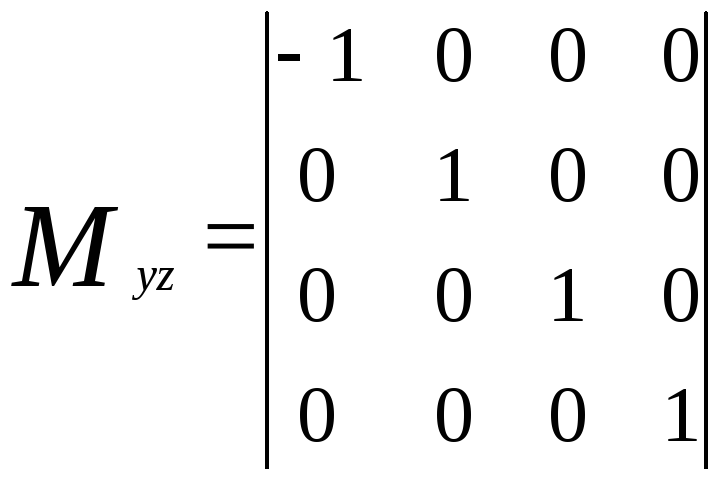
Для плоскости XOZпреобразование отражения представлено в виде

Применяя метод компиляции можно перемножать произвольное число матриц поворота, масштабирования и переноса в трехмерном пространстве XYZ и проецировать результирующую матрицу на плоскость проекции для получения графического изображения Результат всегда будет сводиться к матрице вида [Фоли]:

,

где A, B, C, D, E, G, H, I– параметры поворотов векторов положения всех точек изображения относительно осейX, Y, Z на соответствующие углы;S_x,S_y,S_z - параметры масштабирования по соответствующим осям;t_x , t_y , t_z параметры переноса всех точек объекта на соответствующее смещение вдоль координатных осей.

Проектирование изображения в общем случае можно представить в виде двух процессов: проектирование на плоскости и проектирование в пространстве.

1Поскольку отражение есть частный случай поворота, матрица отражения здесь отдельно не упоминается.